- Introduction
- 1. Introduction to Quantitative Analysis
- 2. Descriptive Statistics
- 3. T-test for Difference in Means and Hypothesis Testing
- 4. Bivariate linear regression models
- 5. Multiple linear regression models
- 6. Assumptions and Violations of Assumptions
- 7. Interactions
- 8. Panel Data, Time-Series Cross-Section Models
- 9. Binary models: Logit
- 10. Frequently Asked Questions
- 11. Optional Material
- 12. Datasets
- 13. R Resources
- 14. References
- Published with GitBook
6. Assumptions and Violations of Assumptions
6.1 Seminar
Setting a Working Directory
Before you begin, make sure to set your working directory to a folder where your course related files such as R scripts and datasets are kept. We recommend that you create a PUBLG100 folder for all your work. Create this folder on N: drive if you're using a UCL computer or somewhere on your local disk if you're using a personal laptop.
Once the folder is created, use the setwd() function in R to set your working directory.
| Recommended Folder Location | R Function | |
|---|---|---|
| UCL Computers | N: Drive | setwd("N:/PUBLG100") |
| Personal Laptop (Windows) | C: Drive | setwd("C:/PUBLG100") |
| Personal Laptop (Mac) | Home Folder | setwd("~/PUBLG100") |
After you've set the working directory, verify it by calling the getwd() function.
getwd()
Now download the R script for this seminar from the "Download .R Script" button above, and save it to your PUBLG100 folder.
# clear environment
rm(list = ls())
Required Packages
Let's start off by installing two new packages that we are going to need for this week's exercises. We'll explain the functionality offered by each package as we go along.
install.packages("lmtest")
Installing package into '/Users/altaf/Library/R/3.2/library'
(as 'lib' is unspecified)
The downloaded binary packages are in
/var/folders/62/x92vvd_n08qb3vw5wb_706h80000gp/T//RtmpfjBoNR/downloaded_packages
install.packages("sandwich")
Installing package into '/Users/altaf/Library/R/3.2/library'
(as 'lib' is unspecified)
The downloaded binary packages are in
/var/folders/62/x92vvd_n08qb3vw5wb_706h80000gp/T//RtmpfjBoNR/downloaded_packages
Now load the packages in this order:
library(lmtest)
library(sandwich)
library(texreg)
Warning: package 'texreg' was built under R version 3.2.3
library(dplyr)
Heteroskedasticity
In order to understand heteroskedasticity, let's start by loading a sample of the U.S. Current Population Survey (CPS) from 2013. The dataset contains 2989 observations of full-time workers with variables including age, gender, years of education and hourly earnings.
income_data <- read.csv("http://uclspp.github.io/PUBLG100/data/cps2013.csv")
Let's explore the dataset by looking at the structure and inspecting the first few observations.
str(income_data)
'data.frame': 2989 obs. of 4 variables:
$ age : int 30 30 30 29 30 30 30 29 29 29 ...
$ gender : Factor w/ 2 levels "Female","Male": 2 2 2 1 2 2 2 1 2 2 ...
$ years_of_education: int 13 12 12 12 14 16 12 14 16 13 ...
$ hourly_earnings : num 12.02 9.86 8.24 10.1 24.04 ...
head(income_data)
age gender years_of_education hourly_earnings
1 30 Male 13 12.019231
2 30 Male 12 9.857142
3 30 Male 12 8.241758
4 29 Female 12 10.096154
5 30 Male 14 24.038462
6 30 Male 16 23.668638
Now plot earnings by years of education.
plot(hourly_earnings ~ years_of_education, data = income_data)
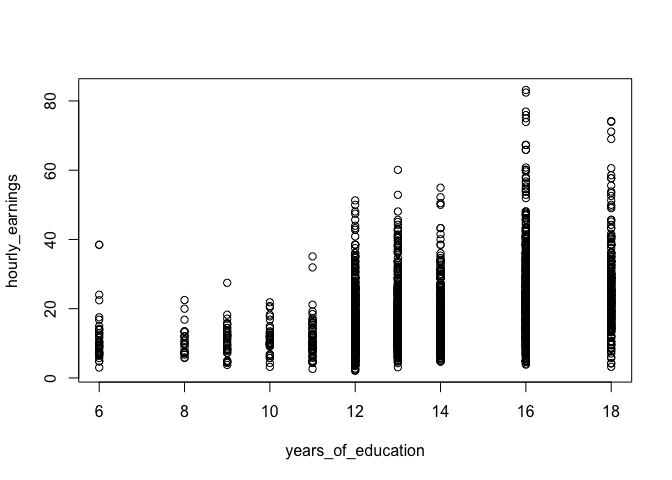
Notice how we're using the formula syntax for the plot() function instead of the normal plot(x, y) syntax that we've used in the past. This is identical to how we specify the independent and dependent variables when running linear regression with the lm() function. The resulting plot is exactly the same as what you would get if you had used the plot(x, y) syntax.
We can see that the range of values for hourly earnings have larger spread as the level of education increases. Intuitively this makes sense as people with more education tend to have more opportunities and are employed in a wider range of professions. But how does this larger spread affect the regression model?
Let's run linear regression and take a look at the results to find out the answer.
model1 <- lm(hourly_earnings ~ years_of_education, data = income_data)
summary(model1)
Call:
lm(formula = hourly_earnings ~ years_of_education, data = income_data)
Residuals:
Min 1Q Median 3Q Max
-23.035 -6.086 -1.573 3.900 60.446
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.37508 1.03258 -5.206 2.07e-07 ***
years_of_education 1.75638 0.07397 23.745 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.496 on 2987 degrees of freedom
Multiple R-squared: 0.1588, Adjusted R-squared: 0.1585
F-statistic: 563.8 on 1 and 2987 DF, p-value: < 2.2e-16
The model tells us the for each additional year of education, the hourly earnings go up by 1.756.
Now let's plot the fitted model on our scatter plot of observations.
plot(hourly_earnings ~ years_of_education, data = income_data)
abline(model1, col = "red")
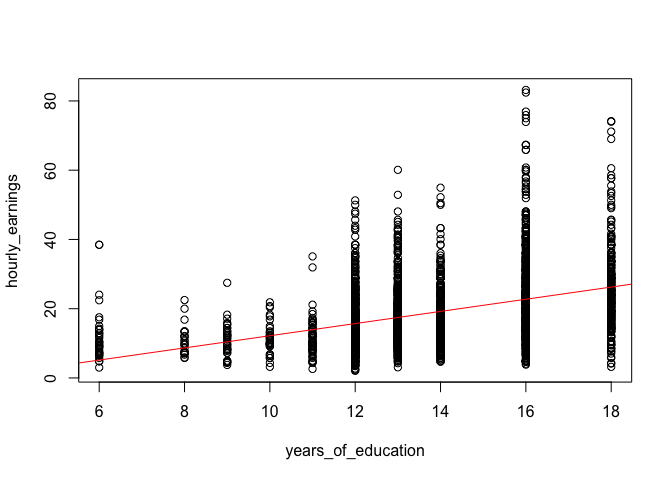
Looking at the fitted model, we can see that the errors (i.e. the differences between the predicted value and the observed value) increase as the level of education increases. This is what is known as heteroskedasticity or heteroskedastic errors. In plain language it simply means that the variability of the error term is not constant across the entire range of our observations.
Another way to visualize this is by plotting residuals against the fitted values.
plot(fitted(model1), residuals(model1), main = "Residuals vs. Fitted")
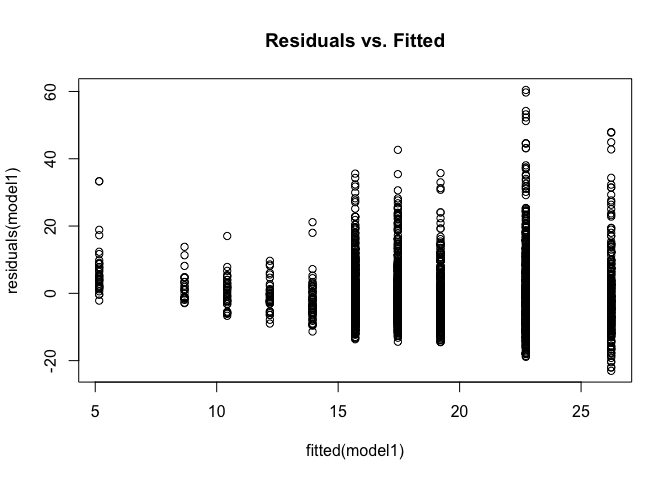
Again, we can see that residuals are not constant and increase as the fitted values increase. In addition to visual inspection, we can also test for heteroskedasticity using the Breusch-Pagan Test from the lmtest package we loaded at the beginning.
bptest(model1)
studentized Breusch-Pagan test
data: model1
BP = 76.679, df = 1, p-value < 2.2e-16
The null hypothesis for the Breusch-Pagan test is that the variance of the error term is constant, or in other words, the errors are homoskedestic. By looking at the p-value from Breusch-Pagan test we can determine whether we have heteroskedastic errors or not.
The p-value tells us that we can reject the null hypothesis of homoskedestic errors. Once we've determined that we're dealing with heteroskedastic errors, we can correct them using the coeftest() function from the lmtest package.
Here is a list of arguments for the coeftest() function:
coeftest(model, vcov)
| Argument | Description |
|---|---|
model |
This is the estimated model obtained from lm(). |
vcov |
Covariance matrix. The simplest way to obtain heteroskedasticity-consistent covariance matrix is by using the vcovHC() function from the sandwich package. The result from vcovHC() can be directly passed to coeftest() as the second argument. |
coeftest(model1, vcov = vcovHC(model1))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.375077 1.047243 -5.1326 3.041e-07 ***
years_of_education 1.756384 0.079985 21.9588 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
After correcting for heteroskedasticity we can see that the standard error for the independent variable years_of_education have increased from 0.074 to 0.08. Even though this increase might seem very small, remember that it is relative to the scale of the independent variable. Since the standard error is the measure of precision for the esitmated coefficients, an increase in standard error means that our original estiamte wasn't as good as we thought it was before we corrected for heteroskedasticity.
Now that we can get heteroskedastic corrected standard errors, how would you present them in a publication (or in the dissertation or the final exam)? Fortunately, all textreg functions such as screenreg() or htmlreg() allow us to easily override the standard errors and p-value in the resulting output.
We first need to save the result from coeftest() to a variable and then override the output from screenreg() by extracting the two columns of interest.
The columns we are interested in are called "Std. Error" and "Pr(>|t|)". There's nothing special about these names, they are obtained simply by looking at the output from coeftest() above.
corrected_errors <- coeftest(model1, vcov = vcovHC(model1))
screenreg(model1,
override.se = corrected_errors[, "Std. Error"],
override.pval = corrected_errors[, "Pr(>|t|)"])
===============================
Model 1
-------------------------------
(Intercept) -5.38 ***
(1.05)
years_of_education 1.76 ***
(0.08)
-------------------------------
R^2 0.16
Adj. R^2 0.16
Num. obs. 2989
RMSE 9.50
===============================
*** p < 0.001, ** p < 0.01, * p < 0.05
Omitted Variable Bias
Ice Cream and Shark Attacks
 Is it true that ice cream consumption increases the likelihood of being attacked by a shark? Let's explore a dataset of shark attacks, ice cream sales and monthly temperatures collected over 7 years to find out.
Is it true that ice cream consumption increases the likelihood of being attacked by a shark? Let's explore a dataset of shark attacks, ice cream sales and monthly temperatures collected over 7 years to find out.
shark_attacks = read.csv("http://uclspp.github.io/PUBLG100/data/shark_attacks.csv")
head(shark_attacks)
Year Month SharkAttacks Temperature IceCreamSales
1 2008 1 25 11.9 76
2 2008 2 28 15.2 79
3 2008 3 32 17.2 91
4 2008 4 35 18.5 95
5 2008 5 38 19.4 103
6 2008 6 41 22.1 108
Run a linear model to see the effects of ice cream consumption on shark attacks.
model1 = lm(SharkAttacks ~ IceCreamSales, data = shark_attacks)
screenreg(model1)
========================
Model 1
------------------------
(Intercept) 4.35
(5.24)
IceCreamSales 0.34 ***
(0.06)
------------------------
R^2 0.29
Adj. R^2 0.28
Num. obs. 84
RMSE 7.17
========================
*** p < 0.001, ** p < 0.01, * p < 0.05
Let's check pairwise correlation between ice cream consumption, average monthly temperatures and shark attacks.
cor(shark_attacks[c("SharkAttacks", "Temperature", "IceCreamSales")])
SharkAttacks Temperature IceCreamSales
SharkAttacks 1.0000000 0.7169660 0.5343576
Temperature 0.7169660 1.0000000 0.5957694
IceCreamSales 0.5343576 0.5957694 1.0000000
It looks like there's high correlation between average monthly temperatures and shark attacks, so let's add the Temperature variable to our model.
model2 = lm(SharkAttacks ~ IceCreamSales + Temperature, data = shark_attacks)
Let's compare it to the first model.
screenreg(list(model1, model2))
===================================
Model 1 Model 2
-----------------------------------
(Intercept) 4.35 0.57
(5.24) (4.31)
IceCreamSales 0.34 *** 0.10
(0.06) (0.06)
Temperature 1.29 ***
(0.20)
-----------------------------------
R^2 0.29 0.53
Adj. R^2 0.28 0.52
Num. obs. 84 84
RMSE 7.17 5.84
===================================
*** p < 0.001, ** p < 0.01, * p < 0.05
The second model shows that once we control for monthly temperatures, ice cream consumption has no effect on the number of shark attacks.
Using pipes with dplyr
Let's go back to the income data from Current Population Survey (CPS) to demonstrate another useful feature that we can use with dplyr. Suppose we wanted to rank the observations in our dataset by income within the respective gender groups. One approach would be to subset the dataset first and then sort them by income.
Without dplyr the solution would look something like this:
First we'd have to subset each category using the subset() function.
subset_men <- subset(income_data, gender == "Male")
subset_women <- subset(income_data, gender == "Female")
Then we would generate the rank for each category.
subset_men$rank <- rank(-subset_men$hourly_earnings, ties.method = "min")
subset_women$rank <- rank(-subset_women$hourly_earnings, ties.method = "min")
Finally, we'd combine the categories to put the dataset back together again.
ranked_data <- rbind(subset_men, subset_women)
This solutions isn't all that bad when dealing with a categorical variable of gender with only two categories. But imagine doing the same with more than two categories (for example, dozens of states or cities) and the solution becomes unmanageable.
Dplyr makes it easy to "chain" functions together using the pipe operator %>%. The following diagram illustrates the general concept of pipes where data flows from one pipe to another until all the processing is completed.
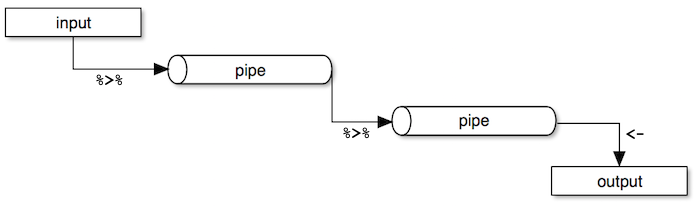
The syntax of the pipe operator %>% might appear unusual at first, but once you get used to it you'll start to appreciate it's power and flexibility.
We're introducing a couple of new functions from dplyr that we'll explain as we go along. For now, let's dive into the code.
ranked_data <- income_data %>%
group_by(gender) %>%
mutate(group_rank = min_rank(desc(hourly_earnings)))
The easiest way to understand the major parts of this code is by following this diagram:
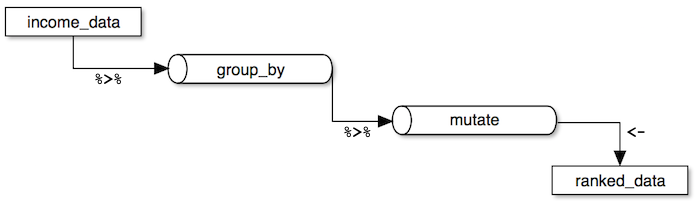
- First,
income_datais fed to the pipe operator. - Then, we group the dataset by
genderusing thegroup_by()function. - Next, we call the
mutate()function to create a new variable calledgroup_rankbased on the descending order ofhourly_earnings. Themutate()function allows you to create new variables or modify existing ones and is especially powerful when combined with other functions such asgroup_by(). - Finally, the result is assigned to
ranked_datavariable.
Now we can easily see the top income earners for each group. We'll use the same pipe operator and chain the filter() function we saw last week with arrange() to sort the results.
ranked_data %>%
filter(gender == "Male") %>%
arrange(group_rank) %>%
head()
Source: local data frame [6 x 5]
Groups: gender [1]
age gender years_of_education hourly_earnings group_rank
(int) (fctr) (int) (dbl) (int)
1 30 Male 16 83.17308 1
2 30 Male 16 82.41758 2
3 30 Male 16 76.92308 3
4 29 Male 16 75.91093 4
5 30 Male 16 75.00000 5
6 29 Male 18 74.17583 6
ranked_data %>%
filter(gender == "Female") %>%
arrange(group_rank) %>%
head()
Source: local data frame [6 x 5]
Groups: gender [1]
age gender years_of_education hourly_earnings group_rank
(int) (fctr) (int) (dbl) (int)
1 30 Female 18 74.00000 1
2 30 Female 16 65.86539 2
3 30 Female 16 65.86539 2
4 29 Female 18 60.57692 4
5 30 Female 18 57.69231 5
6 29 Female 16 55.28846 6
Exercises
Use the World Development Indicators and Polity IV datasets from 2012 to estimate a model explaining the effects of the following variables on levels of democracy. Use
polity2from the Polity IV dataset as the dependant variable. Make sure to test and correct for heteroskedasticity and Omitted Variable Bias.- Unemployment Rate
- Inflation Rate
- Military Expenditure (% GDP)
- Healthcare Expenditure (% GDP)
- Mobile Subscribers (per 100)
Dataset:
NOTE: This exercise will require you to merge the two datasets together. Use
iso3ncountry code as the matching columns for merging.Use the Massachusetts Test Scores dataset from Stock and Watson to fit a model and explain the effects of the following variables on test scores.
- Student-teacher ratio (stratio),
- % English learners (english),
- % Receiving Lunch subsidy (lunch),
- Average District income (income)
NOTE: Use the 8th grade test scores from the variable
score8. The names of explanatory variables are given in parenthesis above:Dataset:
Can the same model be used for California? Why or why not? What assumptions would it violate and how would you correct for them?
Dataset: