Extensions to FTFs in ICECUP 3.1

The new ICECUP 3.1 software provides a number of enhancements to Fuzzy Tree Fragments. ICECUP 3.1 is available with DCPSE and ICE-GB R2 corpora.

These enhancements affect the definition of nodes and words in FTFs. No changes have been made to existing links and edges, the topology or matching of FTFs.

The very latest version of ICECUP, version 3.1.1, provides an additional edge switch for nodes. “Inherit if CJ” allows an FTF node to match coordination patterns as if each coordinated node was a single item rather than a member of a set.

Nodes

In ICECUP 3.0 an FTF node could have an optional single function or category label. It could also have any number of feature labels provided that they were consistent with the category, with only one feature per feature class.

In ICECUP 3.1 an FTF node can now contain a logical combination of node patterns. Each pattern can contain:

• sets of possible functions and categories (optionally, negated)
• any number of features, positive or negative (plus any feature class can be marked as ‘unspecified’)

The following examples illustrate these extensions.

Unspecified

You can search for an unspecified function, category or feature class. Although (in a complete corpus) functions and categories should only be unspecified if the tree is empty, unmarked feature classes are quite common. They may be unspecified because the feature is optional, the element is ambiguous or they may be unmarked in error.

Searching for an unspecified feature class is particularly useful when you want to exhaustively list all subtypes of a particular node pattern. This is labelled IV=0 or DV=0 in the experiment pages. In ICECUP 3.0 you had to calculate the remaining unspecified elements. Now you can obtain the values easily, e.g. “CL(!transy)” finds all clauses whose transitivity has not been marked.

Sets and negation

Function and category sets allow you to easily define broader groupings than those defined by the grammar. For example you may want to embrace all types of direct object “{PROD, NOOD, OD}” within the same query. The easiest way to do this is with a set. A negated set can be used to likewise remove possibilities from a node. Thus “{¬OD,¬SU},CL” is a clause which is anything other than a direct object or subject.

Feature sets can be used to obtain results where different subtypes of features are not of interest, or where the frequency is very low (what is known as ‘collapsing values’). Both intransitive and copular are transitivity features of clauses. The query “CL(intr,cop)” searches for clauses which are either intransitive or copular.

NB. If they belong to different feature classes, as in “N(com,plu)”, features are independent. If they are members of the same class, e.g., “N(com,prop)”, then they are treated as members of a set.

Logic

The introduction of propositional logic into nodes is most useful for the introduction of wholesale negation (where you say a particular node in an FTF may not conform to pattern A) and disjunction (where you say that a node could be either pattern B or pattern C).

The node logic editor in ICECUP 3.1 lets you edit these expressions. It also includes a simplify command which draws out the logical consequences of a particular expression.

Two further extensions

In addition you can specify:

• structural pseudo-features such as “ditto” (‘ditto-tagged’), and
• that any pattern is exactly matched, e.g. “=SU,NP”.

Exact matching works by replacing all unstated features with the explicit unmarked feature class (see above) and removing features which fall within the same feature class.

Words

The second major extension to ICECUP 3.1 is the introduction of an extensive wild card system into the ‘word’ slot in an FTF.

In ICECUP 3.0 you could optionally include a lexical item and these items could be ambiguously matched by case or accent.

ICECUP 3.1 lets you specify sets of wild card patterns (including negated patterns). Each wild card consists of a string of characters optionally including the following special characters.

For more information see ICECUP 3.1: lexical wild cards.

The set representation lets you list alternatives or define a wild card and delete specific alternatives. Moreover, because they are part of an FTF, any lexical pattern can be constrained by the node which tags it. Thus you can write “{*ing ~thing}+<N>” meaning “any -ing noun except ‘thing’.”

ICECUP 3.1.1

‘Inherit if CJ’ edge option

The very latest version of ICECUP, version 3.1.1, provides one further extension to FTFs.

• Normally an FTF node matches a single node in the tree. This is perfectly intuitive. But this 1:1 relationship is not always upheld. Where nodes are ditto-tagged, the same FTF node might match the compound. The reasoning is that “a compound” is really a single grammatical concept realised by more than one word. So the compound a bit is tagged PRON(quant, sing), and a Node search for ‘PRON(quant,sing)’ finds a bit as well as much, a little, a little bit and so on.
• Coordination presents a different problem. A coordinated set includes an additional bracketing node, marked with the feature coordn, and each conjoined item within the set is given the function CJ (conjoin). The problem is that in many cases we should really create two FTFs – one for a regular pattern and one for a coordinated pattern – at any point in a structure which could be coordinated. It is very easy to forget to do this, and cases get missed!

Compare the two examples below.

The difference between the two trees is that the second consists of a series of items of the kind found in the first. But to find both patterns we had to create two FTFs.

This example also shows how information is shared between the upper and lower node in the TOSCA/ICE grammar. The function, ELE (element), is at the top of the entire bracketed structure in the second. But the feature, appos (appositive), is found in the lower node.

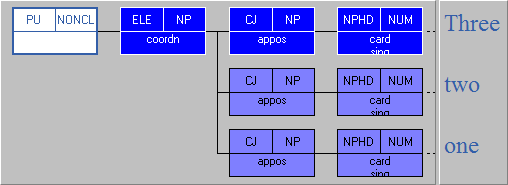
The new inherit if CJ switch solves this problem by employing the new rule illustrated by the scheme below.

With the inherit if CJ option set to Yes, an FTF node is now allowed to match the function of the coordinated group plus the category and features of any single coordinated item. (The category of the coordinated node, which is either the same as the conjoin or disparate, is not considered.) During the search, ICECUP essentially creates a version of the same tree with the single node that would exist were the item not coordinated.

If this FTF node matches across the two nodes, links and edges are then interpreted as if the node were non-coordinated. The Parent, Previous and Next child apply to the upper node (before and after the set). Child and word links apply to the lower (item) node.

For more information, see the ICECUP help in the new version of ICECUP 3.1.1.

FTF home pages by Sean Wallis and Gerry Nelson.
Comments/questions to s.wallis@ucl.ac.uk.

Follow @UCLEnglishUsage

This page last modified 14 May, 2020 by Survey Web Administrator.