We develop physical models that can be used with monitoring data to estimate when a volcano is moving away from its background level of activity and towards conditions favourable for eruption.
Volcalert: Emergency forecasts of volcanic eruptions
Contact Dr Christopher Kilburn (c.kilburn@ucl.ac.uk)
Half of the world’s eruptions are expected to occur at volcanoes that have been quiet for 100 years or more. Most such volcanoes are not regularly monitored and so signs of unrest are usually recorded by emergency networks that can acquire only the most rudimentary information. An urgent need therefore exists for improving the quality of short-term forecasts of eruptions, using emergency data obtained after the start of unrest.
The Volcalert programme specialises in developing physical models of pre-eruptive unrest that can be used with emergency data. A key philosophy is that the results must have an immediate practical value in improving eruption forecasts and, hence, in assisting decision makers to select the most appropriate response to a volcanic emergency. The primary goals, therefore, are to quantify the physical controls on precursors to eruptions and to transform the results into practical forecasting procedures.
For more information see selected references.
- Signs of unrest
Early signs of unrest include: cracks appearing in ground that is being gradually pushed upwards; the occurrence of small earthquakes that can just be felt by those living near a volcano; and the seepage of steam from the surface, sometimes with an underlying smell of sulphur. These signals are triggered when the crust is deformed and fractured by an increase in pressure in a body of underlying magma. The unrest signals are often first detected months before eruption and become more pronounced with time. In extreme cases, however, the precursors can develop from less than an hour (e.g., Mt Hekla, in Iceland (Linde et al., 1993)) to several decades beforehand (e.g., large calderas, such as Campi Flegrei, in Italy (Bellucci et al., 2006), and Rabaul, in Papua New Guinea (Robertson & Kilburn, 2012)).
Local earthquakes (or volcano-tectonic (VT) events) and ground movement are the signals most commonly reported during unrest (Kilburn, 2003, 2012). The earthquakes have typical magnitudes of 2 or less (indicating the movement by millimetres or centimetres of faults ~0.01-0.1 km across), but a proportion may reach magnitudes of 4. They tend to occur in volumes that are kilometres across and in vertical extent; they also normally occur at depths of less than 5-6 km, although they may occasionally be concentrated at deeper levels. As many as ~103-105 VT events can be recorded during a complete sequence and, remarkably, they can occur throughout the volume of crust being deformed without showing a systematic migration in location with time. The corresponding ground movement may be detected over horizontal distances of ~1-10 km, across which maximum values of surface uplift and lateral stretching may reach ~0.1-1 m (e.g., Dzurisin, 2007; Woo & Kilburn, 2010; Bell & Kilburn, 2011).
Associated Papers:
- Modelling precursors
Changes in precursory signal with time
Rates of ground movement and of the occurrence of VT events tend to increase with time before an eruption. The changes show remarkably repetitive behaviour, independent of tectonic setting, magma composition and style of eruption (Tokarev, 1971; Voight, 1988; McNutt, 1996; De la Cruz-Reyna & Reyes-Davila, 2001; Reyes-Davila & De la Cruz-Reyna, 2002; Zobin, 2003). For example, the VT event rate is commonly observed to increase exponentially with time until shortly before eruption, when the rate becomes faster than exponential. The repetitive behaviour strongly suggests not only that short-term forecasts of eruptions are a feasible objective, but also that forecasts can be quantified in a manner that is of practical value.
The Voight criterion
Analyses of precursory trends have been strongly influenced by the Voight criterion (Voight, 1988, 1989), which attributes restricted ranges of precursory behaviour to a positive feedback between the rate and acceleration of a precursor, W:
[Acceleration of W with time] = A [Rate of W with time]a
(1)
where A is a scaling constant that describes the volume of the crust being deformed and a, which usually lies between 1 and 2, describes the specific form of feedback relation. The limits of 1 and 2 correspond to an exponential and to a faster, hyperbolic increase in rate with time. As the rate increases, the acceleration becomes larger, increasing the rate still further. The forecasting potential of the relation depends on estimating when the precursory rate will tend to infinity. This singularity is interpreted to coincide with a major structural change in the crust that may favour an eruption (e.g., the formation of a pathway for magma to reach the surface (Kilburn, 2003)).
Constraints on the Voight criterion
The Voight criterion captures the characteristics of numerous empirical relations that have been proposed for rock deformation and failure (Voight, 1988, 1989; Main, 1999). It was originally proposed (1) that the criterion could be applied to any type of precursory signal (e.g., equating W with the amount of deformation or the number of VT events), and (2) that each precursory sequence was characterised by a single value of a - and, hence, that the behaviour of individual sequences did not evolve with time. Subsequent studies have relaxed these constraints to argue that (1) the criterion applies only to selected precursory signals, the choice of which depends on the conditions of loading (Kilburn, 2012), and (2) individual precursory sequences can evolve with time, such that the value of a may change from 1 to 2 during a sequence (McGuire & Kilburn, 1997; Kilburn & Voight, 1998; Kilburn, 2003).
Associated Papers:
- Physical model
A new physical model from the Volcalert programme
Field observations suggest that the VT precursors are controlled by the slow fracturing of rock around the tips of faults that (1) are distributed throughout the volume of crust being deformed (and, hence, show no preferred migration in location with time) and (2) are much smaller than the deforming volume (so that their collective movements can be modelled by the mean behaviour of the whole population).As part of the Volcalert programme, we have developed a new slow-fracturing model in which the number N of fracturing events changes with stress parameters according to (Kilburn, 2012):
(2)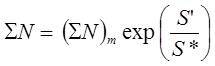
where SN is the cumulative number of VT events (with a value of (SN)m when S’ = 0), S’ is the difference S - sigma;st between the mean applied stress and rock strength; S* = (3kTf + Pc - Pp)/3 is the thermodynamic energy per unit volume stored in the rock due to an absolute temperature T (K) and confining and pore-fluid pressures (Pc and Pp) above zero; the Boltzmann constant k is 1.381 x 1023 J molecule-1 K-1; f is the number of molecules per unit volume and depends on rock chemistry and density; and (dN/dS’)mdenotes the rate when S = σst. The exponential term describes the probability of bulk failure.
Equation (2) integrates a description of macroscopic stress distributions at fault tips (linked to S’) with a description of the potential for atomic bonds to break under a specified mean stress (linked to S* (Kilburn, 2012)). How the rate of fracturing changes with time then depends on how the applied stress or rock strength (both of which will change S’) vary with time.
Field observations suggest that two common loading conditions are deformation (1) at an approximately constant strain rate (Bell & Kilburn, 2011; Kilburn, 2012) and (2) under an approximately constant applied stress (Voight, 1988, 1989; Kilburn, 2003). The first loading condition is consistent with an approximately constant rate of increase in applied stress (say, S = kt), for which Eq. (2) becomes, after differentiation:
(3)
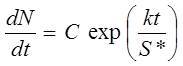
Note that Eqs (3) and (4)-(5) describe the respective changes in mean and peak VT event rate that would be expected for one continuous sequence of earthquakes. In reality, the VT events may occur in a series of episodes, each separated by a time interval of low seismicity. A continuous sequence or series of episodes may both follow a similar trend in the overall cumulative number of VT events with time. Whereas Eq. (2) is expected to be generally applicable, therefore, its derived forms (Eqs (3)-(5)) may only provide good representations of event rate when analysing a single VT episode.
where the constant C = (dN/dt)m exp (σst/S*). The VT event rate is thus expected to increase exponentially with time, corresponding to the Voight criterion with a = 1.
For creep deformation under a constant applied stress, the rate of fracturing depends on stresses remaining sufficiently concentrated around the tips of faults so that the surrounding rock can continue to fracture and allow faults to slip (Kilburn, 2003). Under this condition, it is important to accommodate fluctuations in event rate with time by using the peak event rate (dNcr/dt)p as the diagnostic measure, for which S’ reduces to p (σst2/Y) Ncr and Eq. (2) yields
(4)
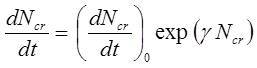
where g* = (p/S*) (sst2/Y), (dNh/dt)p,0 is the peak event rate at the start of the faster-than-exponential sequence and Y is Young’s modulus. Eq. (4) can be re-expressed as:
(5)
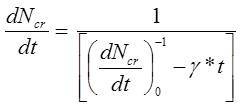
which describes a hyperbolic increase in VT event rate with time and is consistent with the Voight criterion for a = 2 (Kilburn, 2003).
Associated Papers:
- Choice of precursor
Which trend will a precursor follow?
The theoretical expressions for changes in event rate with time (Eqs (3) to (5)) are derived from the parent relation for changes in event rate with stress (Eq. (1). It was then assumed that the rate of applied stress increase was constant with time, to obtain the exponential time trend in Eq. (3), and the applied stress was constant, to obtain the faster-than-exponential time trend in Eq. (5).
The contemporaneous changes in deformation rate with time are different for each of the assumed conditions.
(1) For small amounts of damage (fracturing of rock over distances at least ten times smaller than the length of the zone around a fault tip in which stresses become concentrated), rates of deformation increase in proportion with rates of stress. In this case, exponential increases in VT event rate will be accompanied by an approximately constant rate of deformation. Hence, the VT event rate will follow the Voight criterion for a = 1, while the constant deformation rate will not be described by the Voight criterion (Kilburn, 2012).
(2) Under a constant stress, in contrast, the amount of elastic deformation of unbroken rock remains constant, by definition. Observed changes in deformation rate are thus controlled by the rate of fault movement through additional fracturing (inelastic deformation). In this case, it is possible for the VT event rate and the deformation rate to increase in proportion with each other. Hence, if the VT event rate follows the Voight criterion for a = 2, it is possible that the deformation rate will also be described by the same condition for a.
The key inference here is that the Voight criterion cannot be applied universally to all precursors. Its applicability to a particular precursor depends on the conditions of loading and so must be evaluated on a case-by-case basis.
- Forecasting eruptions
Short-term precursors: volcano-tectonic events
Precursory unrest commonly continues for several months. During this time, volcano-tectonic events may be concentrated in shorter episodes separated by intervals of low seismicity. The VT episodes and intervals may both last for days or weeks. VT event rates tend to increase with time during each episode and their maximum values tend to increase from one episode to the next. When the sequences and intervals are considered together, the overall cumulative number of VT events frequently shows an exponential increase with time (as described by Eq. (2) in the section on modelling precursory behaviour). Successive sequences are thus unlikely to be independent from each other, but instead belong to a common, longer-term trend.
Within hours or days before eruption, the final sequence of VT events usually shows an increase in rate that is faster than exponential. Two broad types of faster-than-exponential (FTE) trend have been recognised: an abrupt, step-like increase within a day or less of the eruption, or a hyperbolic increase that evolves some 10-14 days beforehand. The abrupt trend appears to be common at frequently-erupting basaltic volcanoes, including Kilauea (Bell & Kilburn, 2011) and Mt Etna (Wall et al., 2012), whereas the hyperbolic trend has been observed at andesitic-dacitic volcanoes reawakening after centuries of repose, such as Mt Pinatubo (Philippines) in 1991 and Soufriere Hills (Montserrat) in 1995 (Kilburn, 2003; Smith & Kilburn, 2010).
Warning times
FTE behaviour in VT event rate is a natural indicator that an eruption might be imminent. However, the start of an FTE trend may be indistinguishable from a temporary burst in VT events. Some time is thus required to confirm whether an FTE trend has developed. For abrupt FTE behaviour, the confirmation time may be comparable to the duration of the whole sequence, so that relying on an FTE trend may yield a warning time of hours or less (Bell & Kilburn, 2013). For hyperbolic FTE behaviour, a week or more may be required to confirm the trend, so that the useful warning time may be reduced to two or three days (Kilburn, 2003; Kilburn & Sammonds, 2005).
Even if confirmation times could be reduced, practical limits on issuing warnings from FTE trends remain constrained to days or less by the physics of rock fracture. For the warning times to be increased, additional criteria must be identified for using preceding precursory trends to forecast when the final FTE stage will be reached. Such criteria may include defining a threshold amount of deformation or seismic energy release, beyond which bulk failure of the crust and the formation of a new magmatic pathway can be expected (Yokoyama, 1988).
If additional criteria cannot be established, then warning times of more than a few days will necessarily rely on probabilistic assessments based on empirical data (Sparks, 2003; Grasso & Zaliapin, 2004). By their very nature, probabilistic assessments will require decision-makers to accept a higher chance of false alarms than from deterministic models alone. This consequence is inevitable if long warning times are demanded.
Real-time forecasting
See the animated powerpoint presentation to explore the practical constraints on warning times from a hyperbolic FTE trend. New developments in real-time forecasting can be followed on the website for Project EFFORT, a NERC-funded collaboration between the University of Edinburgh and UCL.
Long-term precursors
The evolution of precursory signals over decades is discussed on our caldera webpage.
Associated Papers:
- Experiments
Field observations of precursors provide information on rock fracture (through VT events) and deformation (through ground movement). However, they do not provide direct measurements of applied stress. The relations between precursory signals and stress are determined instead using data from controlled experiments on rock fracture in the laboratory. Thus Eq. (2) in the section on modelling precursory behaviour was first developed and tested against published data from experiments by Scholz (1968), Ohnaka and Mogi (1982), Meredith et al. (1990), Zang et al. (1998), and Smith et al. (2009).
The experiments were conducted on a range of common crustal rocks in compression. In the field, however, the crust deforms in extension above a pressurized magma body. In collaboration with UCL’s Rock & Ice Physics Laboratory, therefore, we have developed a novel experimental arrangement for rock failure in extension. Initial results indicate that our theoretical model is indeed consistent with extensional rock failure, so supporting its application also to field conditions (Wall et al., 2012).
Associated Papers:
Selected References:
For additional sources, see references in cited publications.
Precursors to dyke-fed eruptions at basaltic volcanoes: insights from patterns of volcano-tectonic seismicity at Kilauea volcano, Hawaii. Bull Volcanol, 74: 325-339, doi 10.1007/s00445-011-0519-3.Trends in the aggregated rate of pre-eruptive volcano-tectonic seismicity at Kilauea volcano, Hawaii. Bull Volcanol, 75: doi 10.1007/s00445-012-0677-yDe la Cruz-Reyna S, Reyes-Davila GA (2001)
A model to describe precursory material-failure phenomena: applications to short-term forecasting at Colima volcano, Mexico. Bull Volcanol 63: 297-308.
Grasso JR, Zaliapin I (2004)
Predictability of volcano eruption: lessons from basaltic volcanoes, Geophys Res Lett, 31: doi 10.1029/2003GL019022.
Linde AT, Agustsson K, Stefansson R (1993)
Mechanism of the 1991 eruption of Hekla from continuous borehole strain monitoring. Nature, 365: 737-740, doi 10.1038/365737a0.
Main IG (1999)
Applicability of time-to-failure analysis to accelerated strain before earthquakes and volcanic eruptions. Geophys J Int, 139: F1-F6.
McNutt SR (1996)
Seismic monitoring and eruption forecasting of volcanoes: a review and state-of-the-art and case histories. In: Scarpa R, Tilling RI (eds) Monitoring and mitigation of volcano hazards. Springer, Berlin, pp 99-146.
Meredith PG, Main IG, Jones C (1990).
Temporal variations in seismicity during quasi-static and dynamic rock failure. Tectonophysics, 175: 249-268.
Ohnaka M, Mogi K (1982)
Frequency characteristics of acoustic emission in rocks under uniaxial compression and its relation to the fracturing process to failure. J Geophys Res, 87: 3873-3884.
Scholz CH (1968)
Microfracturing and the inelastic deformation of a rock in compression. J Geophys Res, 73: 1417-1432.
Sparks RSJ (2003)
Forecasting volcanic eruptions. Earth Planet Sci Lett, 210: 1-15, doi 10.1016/S0012-812X(03)00124-9.
Tokarev PI (1971)
Forecasting volcanic eruptions from seismic data. Bull Volcanol 35: 243-250.
Voight B (1988)
A method for prediction of volcanic-eruptions. Nature. 332: 125-130.
Voight B (1989)
A relation to describe rate-dependent material failure. Science, 243: 200-203.
Yokoyama I (1988) Seismic energy releases from volcanoes. Bull Volcanol, 50: 1–13.
Zang A, Wagner FC, Stanchits S, Dresen G, Andresen R, Haidekker MA (1998) Source analysis of acoustic emissions in Aue granite cores under symmetric and asymmetric compressive loads. J Geophys Res, 135: 1113-1130.
Zobin VM (2003) Introduction to volcanic seismology. Elsevier, Amsterdam, The Netherlands.
 Close
Close


