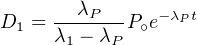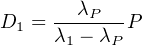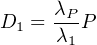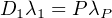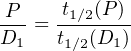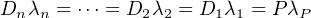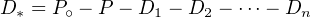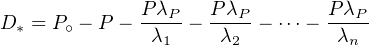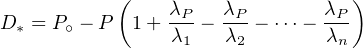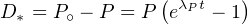Chapter 2
Basic notions of radiometric geochronology
2.1 Isotopes and radioactivity
Thanks to discoveries by Niels Bohr, Ernest Rutherford, Arnold
Sommerfeld, Joseph Thomson and James Chadwick, we know that rocks
and minerals are made of atoms, atoms are made of a nucleus and an
electron cloud, and the nucleus is made of nucleons of which there are two
kinds: protons and neutrons. The total number of nucleons in the atomic
nucleus is called the mass number (A). The number of protons (which
equals the number of electrons in a neutral atom) is called the atomic
number (Z). The chemical properties of a nuclide solely depend on the
atomic number, which therefore forms the basis of the Periodic Table
of Elements. The number of neutrons in the atomic nucleus may
take on a range of values for any given element, corresponding to
different isotopes of said element. For example, 816O is an isotope of
oxygen with 16 nucleons of which 8 are protons (and N = A-Z =
16-8 = 8 are neutrons). Adding one extra neutron to the nucleus
produces a second oxygen isotope, 817O, with identical chemical
properties as 816O, but slightly different physical properties (e.g. boiling
temperature). Adding another neutron produces 818O which, with 8
protons and 10 neutrons, is more than 10% heavier than 816O.
Due to this mass difference, the 818O/ 816O ratio undergoes mass
fractionation by several natural processes, forming the basis of 818O/ 816O
palaeothermometry (see the second half of this course). When we try to add
yet another neutron to the atomic nucleus of oxygen, the nucleus becomes
unstable and undergoes radioactive decay. Therefore, no 819O exists in
nature.
2.2 Radioactivity
As mentioned before, the Periodic Table of Elements (aka ‘Mendeleev’s
Table’) arranges the elements according to the atomic number and the
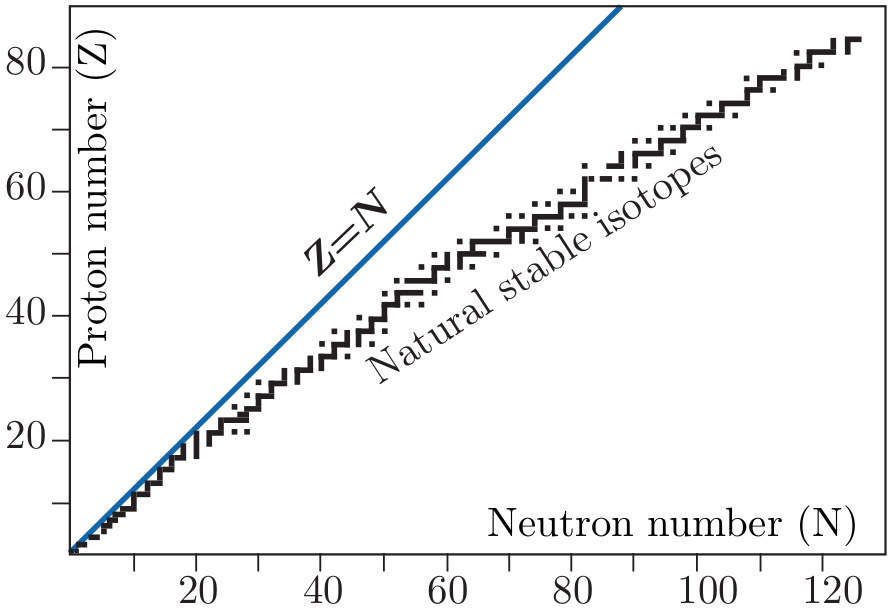
configuration of the electron cloud. The equally important Chart
of Nuclides uses both the number of protons and neutrons as row
and column indices. At low masses, the stable nuclides are found
close to the 1 ÷ 1 line (N ≈ Z), with the radionuclides found at
higher and lower ratios. At higher atomic numbers, the stable nuclides
are found at higher mass numbers, reflecting the fact that more
neutrons are required to keep the protons together. For example,
82208Pb, which is the heaviest stable nuclide, has 44 more neutrons than
protons. The unstable nuclides (or radionuclides), such as 82209Pb or
819O may survive for time periods of femtoseconds to billions of
years depending on the degree of instability, which generally scales
with the ‘distance’ from the curve of stable nuclides. Radionuclides
eventually disintegrate to a stable form by means of a number of different
mechanisms:
- α-decay
The atomic nucleus (e.g., 92238U, 92235U, 90232Th, 62147Sm)
loses an α particle, i.e. the equivalent of a 24He nucleus. When
these nuclei acquire electrons, they turn into Helium atoms,
forming the basis of the U-Th-He chronometer, which is further
discussed in Section 7.1. The recoil energy of the decay is
divided between the α particle and the parent nucleus, which
eventually relaxes into its ground state by emitting γ-radiation,
i.e. photons with a wavelength of 10-12m or less. In addition
to the aforementioned U-Th-He method, α-decay is central
to the 147Sm-143Nd (Section 4.2), 235U-207Pb, 238U-206Pb and
232Th-208Pb methods (Section 5).
- β-decay
Comprises negatron (β-) and positron (β+) emission, in which
either an electron or a positron is emitted from the nucleus,
causing a transition of (N,Z) → (N-1,Z+1) for β- decay and
(N,Z) → (N+1,Z-1) for β+ decay. For example, the oxygen isotope
819O discussed in Section 2.1 decays to 919F by β- emission.
In contrast with α particles, which are characterized by discrete
energy levels, β particles are characterised by a continuous energy
spectrum. The difference between the maximum kinetic energy
and the actual kinetic energy of any given emitted electron
or positron is carried by a neutrino (for β+ decay) or an
anti-neutrino (for β- decay). Just like α decay, β decay is
also accompanied by γ-radiation, arising from two sources: (a)
relaxation into the ground state of the excited parent nucleus and
(b) spontaneous annihilation of the unstable positron in β+ decay.
β- decay is important for the 40K-40Ca, 87Rb-87Sr (Section 4.2)
and 14C-14N (Section 4.1) clocks. It also occurs as part of the
235U-207Pb, 238U-206Pb and 232Th-208Pb decay series (Sections 5
and 9). β+ decay is found in the 40K-40Ar system (Section 6).
- electron capture
This is a special form of decay in which an ‘extra-nuclear’ electron
(generally from the K-shell) is captured by the nucleus. This
causes a transformation of (N,Z) → (N+1,Z-1), similar to positron
emission, with which it often co-exists. The vacant electron
position in the K-shell is filled with an electron from a higher shell,
releasing X-rays (~ 10-10m wavelength), which is the diagnostic
signal of electron capture. This mechanism occurs in the 40K-40Ar
decay scheme (Section 6).
- nuclear fission
Extremely large nuclei may disintegrate into two daughter nuclei
of unequal size, releasing large amounts of energy (~ 200 MeV).
The two daughter nuclei move in opposite directions from the
parent location, damaging the crystal lattice of the host mineral
in their wake. The two daughter nuclides are generally radioactive
themselves, giving rise to β-radiation before coming to rest as
stable isotopes. 92238U is the only naturally occurring nuclide
that undergoes this type of radioactive decay in measurable
quantities, and even then it only occurs once for every ~2×106
α-decay events. Nevertheless, the fission mechanism forms the
basis of an important geochronological method, in which the
damage zones or ‘fission tracks’ are counted (Section 7.2). Nuclear
fission can also be artificially induced, by neutron irradiation of
235U, e.g.:
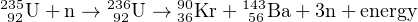 | (2.1) |
Note that every neutron on the left hand side of this formula
generates three neutrons on the right hand side. The latter may react
with further 235U nuclei and generate a chain reaction. This forms the
basis of nuclear reactors, the atom bomb and the ‘external detector’
method (Section 7.2).
2.3 The age equation
A characteristic property of radioactive decay is its absolute independence
of external physical and chemical effects. In other words, it is not affected
by changes in pressure, temperature, or the molecular bonds connecting a
radioactive nuclide to neighbouring atoms. This means that the rate at
which a radioactive parent decays to a radiogenic daughter per unit time,
i.e. dP∕dt only depends on P, the number of parent atoms present. The
decay constant λ expresses the likelihood that a radioactive disintegration
takes place in any given time (i.e., λ has units of atoms per atoms per year).
This can be expressed mathematically with the following differential
equation:
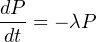 | (2.2) |
Integrating this equation over time yields:
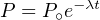 | (2.3) |
where P∘ is the number of parent atoms present at time t = 0. Since this
number is generally unknown (one exception is 14C, see Section 4.1),
Equation 2.3 generally cannot be used in this form. We can, however,
measure the present number of parent and daughter nuclides in the sample.
Rewriting Equation 2.3:
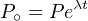 | (2.4) |
and bearing in mind that P∘ = P + D, we obtain:
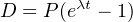 | (2.5) |
This equation forms the foundation of most geochronological methods. It
can be rewritten explicitly as a function of time:
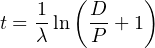 | (2.6) |
The degree of instability of a radioactive nuclide can be expressed
by λ or by the half life t1∕2, which is the time required for half of
the parent nuclides to decay. This follows directly from Equation
2.3:
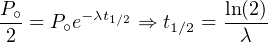 | (2.7) |
As a rule of thumb, the detection limit of a radiometric geochronometer
is reached after about 10 half lives. Thus, 14C goes back ~50,000 years,
10Be 10 million and 40K 10 billion years.
2.4 Decay series
Sometimes the radiogenic daughter (D1) of a radioactive parent is
radioactive as well, decaying to a daughter of its own (D2), which may be
radioactive again etc., until a stable daughter (D*) is reached. Considering
the simplest case of one intermediate daughter:
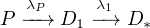 | (2.8) |
The increase (or decrease) of the number of atoms per unit time for each
of the nuclides is given by:
| for P | : dP∕dt = -λPP | (2.9)
|
| for D1 | : dD1∕dt = λPP - λ1D1 | (2.10)
|
| for D* | : dD*∕dt = λ1D1 | (2.11) |
The number of parent atoms P can be written as a function of
t:
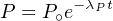 | (2.12) |
Plugging Equation 2.12 into 2.10 yields
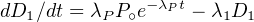 | (2.13) |
Solving this differential equation yields the evolution of D1 with time.
Assuming that D1 = 0 at t = 0:
![D = ---λP--P [e- λPt - e-λ1t]
1 λ1 - λP ∘](index10x.png) | (2.14) |
If λP ≪ λ1 (by a factor of 10 or greater), then e-λ1t becomes
vanishingly small relative to e-λPt after a sufficiently long time so that
Equation 2.14 can be simplified:
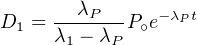 | (2.15) |
or, alternatively:
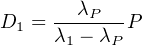 | (2.16) |
This means that the ratio of D1 and P remains constant through time.
If λP ≪ λ1, then λ1 - λP ≈ λ1, from which it follows that:
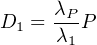 | (2.17) |
Rearranging:
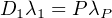 | (2.18) |
or, equivalently:
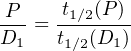 | (2.19) |
This is the secular equilibrium in which the number of atoms of both
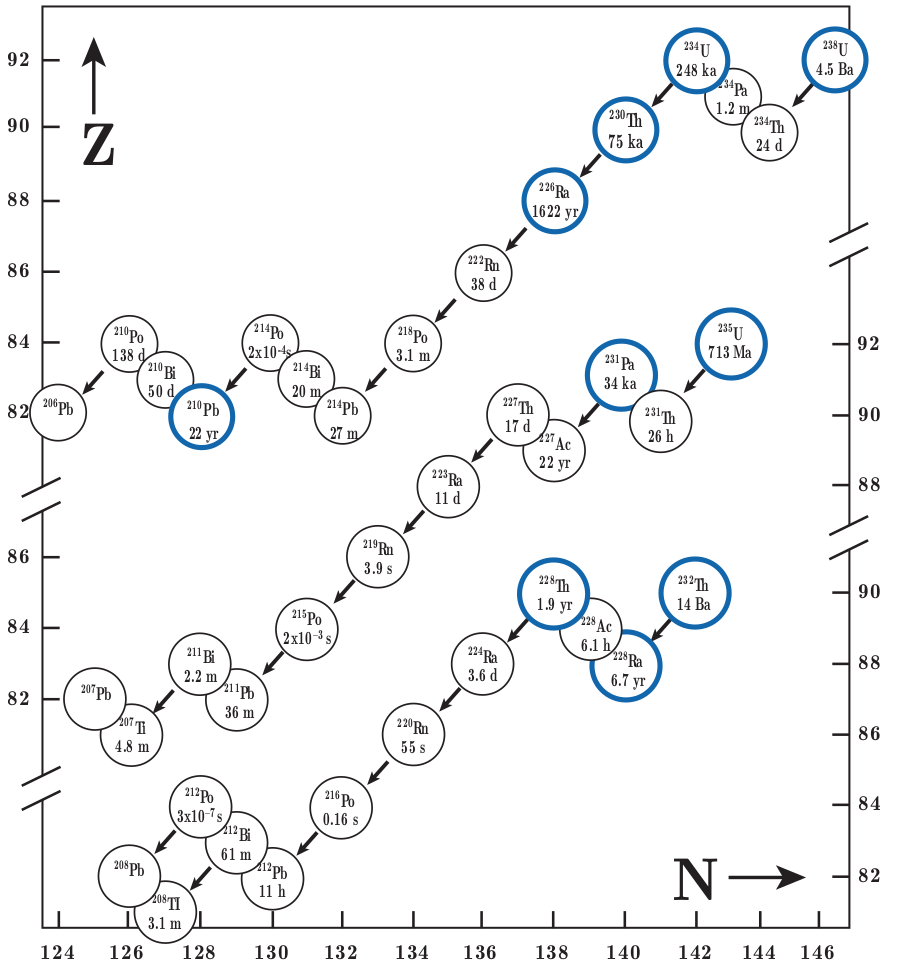
radioactive members is proportional to their respective half lives. In the
geochronological isotope systems 235U/207Pb, 238U/206Pb and 232Th/207Pb,
the lead isotopes are the end points of a long decay series comprised of
several α and β- disintegrations, in which the decay constants of the parent
nuclide is orders of magnitude shorter than the other nuclides in the
chain. For a decay series like that, Equation 2.18 can be generalised
to:
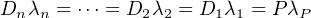 | (2.20) |
This means that the entire series is in equilibrium, so that all members
occur in mutually constant proportions. The number of atoms of the stable
end member D* is given by:
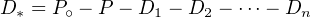 | (2.21) |
Using Equation 2.20, this becomes:
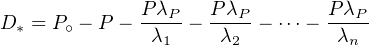 | (2.22) |
or
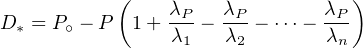 | (2.23) |
Since each of the ratios λP∕λ1, λP∕λ2, etc. are vanishingly small, we can
simplify Equation 2.23 as:
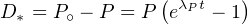 | (2.24) |
This means that the accumulation of the final Pb isotope of the
aforementioned three decay series is only a function of the decay of the
parent isotope. All intermediate decay steps are therefore inconsequential.
In rare cases, however, the isotopic equilibrium is disturbed by a dissolution
or recrystallisation event, say. The intermediate parent/daughter
pairs can then be used to date phenomena occurring over much
shorter time scales than those probed by the U-Pb method (Section
9).
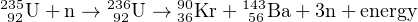
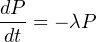
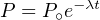
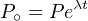
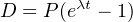
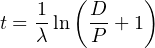
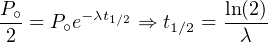
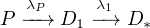
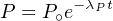
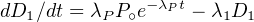
![D = ---λP--P [e- λPt - e-λ1t]
1 λ1 - λP ∘](index10x.png)