Chapter 6
The K-Ar system

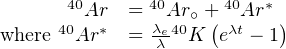
Potassium has three naturally occurring isotopes: ³⁹K, ⁴⁰K and ⁴¹K. ⁴⁰K is radioactive and undergoes branched decay to ⁴⁰Ca (by electron emission λ_β- = 4.962 × 10^-10yr^-1) and ⁴⁰Ar (by electron capture λ_e = 0.581 × 10^-10yr^-1) with a combined half life of 1.248 billion years. The positron emission mechanism mentioned in Chapter 2.2 has an extremely long half life and can therefore safely be neglected. In addition to ⁴⁰Ar, argon has two more stable isotopes: ³⁶Ar and ³⁸Ar. Argon makes up ~1% of the terrestrial atmosphere, with a fixed isotopic composition of ⁴⁰Ar/³⁶Ar = 298.5 and ³⁸Ar/³⁶Ar = 0.187. The argon contained in K-bearing minerals is made up of a mixture of radiogenic (⁴⁰Ar^*) and non-radiogenic gas (⁴⁰Ar_∘):

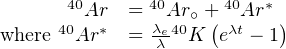(6.1)

with λ the total decay constant of ⁴⁰K (λ = λ_e + λ_β- = 5.543 × 10^-10yr^-1).

6.1 K-Ar dating

The ⁴⁰K →⁴⁰Ar^* decay scheme forms the basis of the K-Ar geochronometer, with the following age equation:

(6.2)

Taking into account the ‘contaminated’ (aka ‘excess’ or ‘inherited’) argon component ⁴⁰Ar_∘ and analysing several cogenetic rocks or minerals with different K (and therefore ⁴⁰Ar^*) contents, an isochron equation can be formed by division through ³⁶Ar:

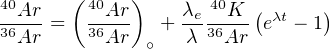(6.3)

which can be solved for t. Alternatively, we can simply assume that all the inherited argon has an atmospheric origin, so that (⁴⁰Ar∕³⁶Ar)_∘ = 298.5.

6.2 ⁴⁰Ar/³⁹Ar dating

From an analytical perspective, K-Ar dating is a two step process. Because K (an alkali metal) and Ar (a noble gas) cannot be measured on the same analytical equipment, they must be analysed separately on two different aliquots of the same sample. This limitation is overcome by the ⁴⁰Ar/³⁹Ar technique, which is a clever variation of the K-Ar method. The idea is to subject the sample to neutron irradiation and convert a small fraction of the ³⁹K to synthetic ³⁹Ar, which has a half life of 269 years. The age equation can then be rewritten as follows:

(6.4)

where ‘x’ stands for ‘sample’ and J is a constant of proportionality which encapsulates the efficiency of the ³⁹K (n,p) ³⁹Ar reaction and into which the factor λ∕λ_e is folded as well. The J-value can be determined by analysing a standard of known age t_s which was co-irradiated with the sample:

(6.5)

In which the subscript ‘s’ stands for ‘standard’. The great advantage of equation 6.4 over 6.2 is that all measurements can be completed on the same aliquot and using a single instrument, namely a noble gas mass spectrometer, which can analyse extremely small (down to μg-sized) samples.

The ⁴⁰Ar/³⁹Ar-method also allows the analyst to investigate the extent of argon loss by means of stepwise heating experiments. This is done by degassing the sample under ultra-high vacuum conditions in a resistance furnace. At low temperatures, the weakly bound Ar is released, whereas the strongly bound Ar is released from the crystal lattice at high temperatures until the sample eventually melts. Plotting the apparent ages against the cumulative fraction of ³⁹Ar released yields an ⁴⁰Ar/³⁹Ar age spectrum (Figure 6.1). If a rock or mineral has remained closed since its formation, the ⁴⁰Ar/³⁹Ar-ratio should remain constant over the course of the different heating steps, forming an ‘age plateau’. More complex (e.g. rising) release spectra, on the other hand, are diagnostic of complex thermal histories featuring partial argon loss. ‘saddle’ shaped release spectra are indicative of ‘excess’ argon. The composition of the inherited argon gas can be determined using a variant of the isochron method, assuming that all ³⁶Ar is inherited:

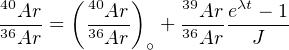(6.6)

If the Ar contamination is constant throughout the entire sample, then the 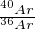-measurements will be arranged along a linear trend whose slope is a function of 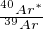and, hence, the age.

6.3 Applications

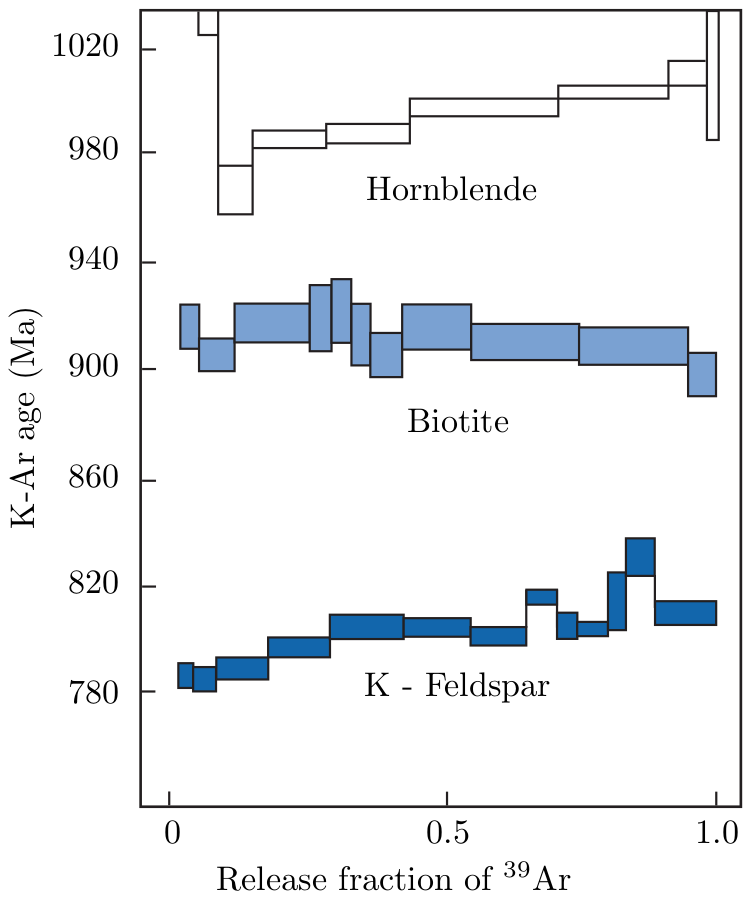
The K-Ar and ⁴⁰Ar/³⁹Ar-methods are some of the most widely used geochronometers and important tools in the calibration of the geologic time scale. The method is applicable to rocks and minerals > 10⁶yr. Obviously, younger materials require more careful treatment of the inherited argon components.

• Magmatic rocks: formation ages can only be obtained for rapidly cooled volcanic rocks, using either mineral separates (sanidine, biotite, hornblende) or whole rocks. Pyroclastics and obsidian may yield reliable ages only if they are unaltered and contain little non-radiogenic argon. Plutonic rocks typically cool much slower than volcanic rocks and generally yield cooling ages rather than formation ages.
• Sedimentary rocks: K-Ar dating of authigenic mineral phases has often been attempted but remains difficult. Glauconite has been used successfully in some cases. Dating detrital minerals such as white mica (muscovite, phengite) in fluvial sediments is frequently used to study the metamorphic history of the hinterland.
• Metamorphic rocks: pelitic metamorphic rocks tend to be rich in K-bearing micas and amphiboles, which can easily be dated with the K-Ar and ⁴⁰Ar/³⁹Ar methods, but require careful interpretation. In high grade metamorphic terranes, the apparent ages can either reflect the metamorphic crystallisation history or the postmetamorphic cooling history. Low grade metamorphic terranes, on the other hand, carry a risk of containing inherited argon components from previous evolutionary stages.