![4He = [8137.818(eλ238t - 1)+ 7--1--(eλ235t - 1)]U +
138.818 138.818
6(eλ232t - 1)Th +0.1499(eλ147t - 1)Sm](index64x.png)
The temperature sensitivity of the K-Ar system (Section 6) is a characteristic feature not only of this method, but of a separate class of geochronometers known as ‘thermochronometers’. The most important of these methods are the U-Th-He 7.1 and fission track 7.2 techniques, which are becoming increasingly popular as a means of investigating Earth surface processes.
When U and Th decay to various isotopes of Pb (Section 5.1), they do so by α-emission (Section 2.2). When α particles acquire electrons, they become helium atoms. Thus, not only Pb content, but also the He content increases relative to U and Th through time, forming the basis of the U-Th-He chronometer:
![4He = [8137.818(eλ238t - 1)+ 7--1--(eλ235t - 1)]U +
138.818 138.818
6(eλ232t - 1)Th +0.1499(eλ147t - 1)Sm](index64x.png) | (7.1) |
Where the values ‘8’, ‘7’ and ‘6’ refer to the number of α-particles
produced in the decay chains of 238U, 235U and 232Th, respectively (Figure
2.2), 137.818 is the (average) ratio of naturally occurring 238U and 235U in
accessory minerals, and the last term accounts for the (often negligible)
accumulation of helium by Sm-decay (Section 4.4). It was Ernest
Rutherford who first proposed that the U-Th-He decay scheme could be
used as an absolute dating technique, making it the oldest radiometric
chronometer. Early experiments on uraninite (UO2) by Robert John Strutt
(4th Baron Rayleigh) at Imperial College London in 1905 yielded ages that
were systematically too young. This was correctly attributed to the volatile
nature of the helium atom, which diffuses out of most minerals at low
temperatures and therefore yields only minimum ages. As a result, the
method was largely abandoned until 1987, when American geochronologist
Peter Zeitler realised that this ‘leaky’ behaviour provided a powerful
means of reconstructing the thermal evolution of rocks and minerals.
Let C(x,y,z) be the He-concentration as a function of the spatial coordinates x, y and z. The evolution of C with time (t) is given by the diffusion equation (‘Fick’s law’):
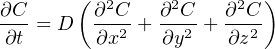 | (7.2) |
Where D is the ‘diffusion coefficient’, which varies exponentially with temperature (T) according to the ‘Arrhenius Law’:
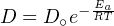 | (7.3) |
with D∘ the ‘frequency factor’, Ea the ‘activation energy’ and R the ideal gas constant (8.3144621 J/mol.K). By taking the logarithm of both sides of Equation 7.3, we obtain (Figure 7.1):
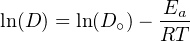 | (7.4) |
Both the frequency factor and the activation energy can be determined
from diffusion experiments, in which a He-bearing mineral is subjected to a
step-heating experiment similar to the kind we saw in the 40Ar/39Ar
method (Section 6.2).
Let us now consider the situation of a mineral which (a) accumulates He through radioactive decay of U and Th, (b) loses He by thermal diffusion, and (c) undergoes monotonic cooling at a variable rate dT/dt. At high temperatures, the He will be lost quickly but as time progresses, the thermal diffusion becomes increasingly sluggish until the He is eventually ‘locked’ into the crystal lattice and the isotopic system is effectively closed. If the thermal history is so that 1/T increases linearly with time, then it is possible to calculate an equivalent ‘closure temperature’ Tc. This is known as ‘Dodson’s equation’:
 | (7.5) |
where r = is the effective grain size (radius) of the mineral and A is a
geometric factor (55 for a sphere, 27 for a cylinder and 8.7 for a
plane sheet). Thus the U-Th-He age calculated at the end of the
aforementioned thermal history equals that which would have been
obtained if He accumulated linearly since the rock passed through
Tc.
Although the closure temperature concept is an oversimplification of reality, it has great intuitive appeal. Consider, for example, a vertical transect in a rapidly exhuming mountain range. The apparent U-Th-He ages along such a transect are approximately given by the time elapsed since the respective rocks have passed through Tc. For apatite [Ca5(PO4)3(OH,F,Cl)], this is ~ 60∘C, which corresponds to a depth (assuming a thermal gradient of 30∘C/km) of 1.5-2km. Thus, the rocks at the high elevations along the transect will have passed through Tc before those collected at the bottom of the transect, and the corresponding U-Th-He ages will therefore increase with elevation. Moreover, the rate of increase of age increase with elevation can be used to estimate the exhumation rate of the orogen.
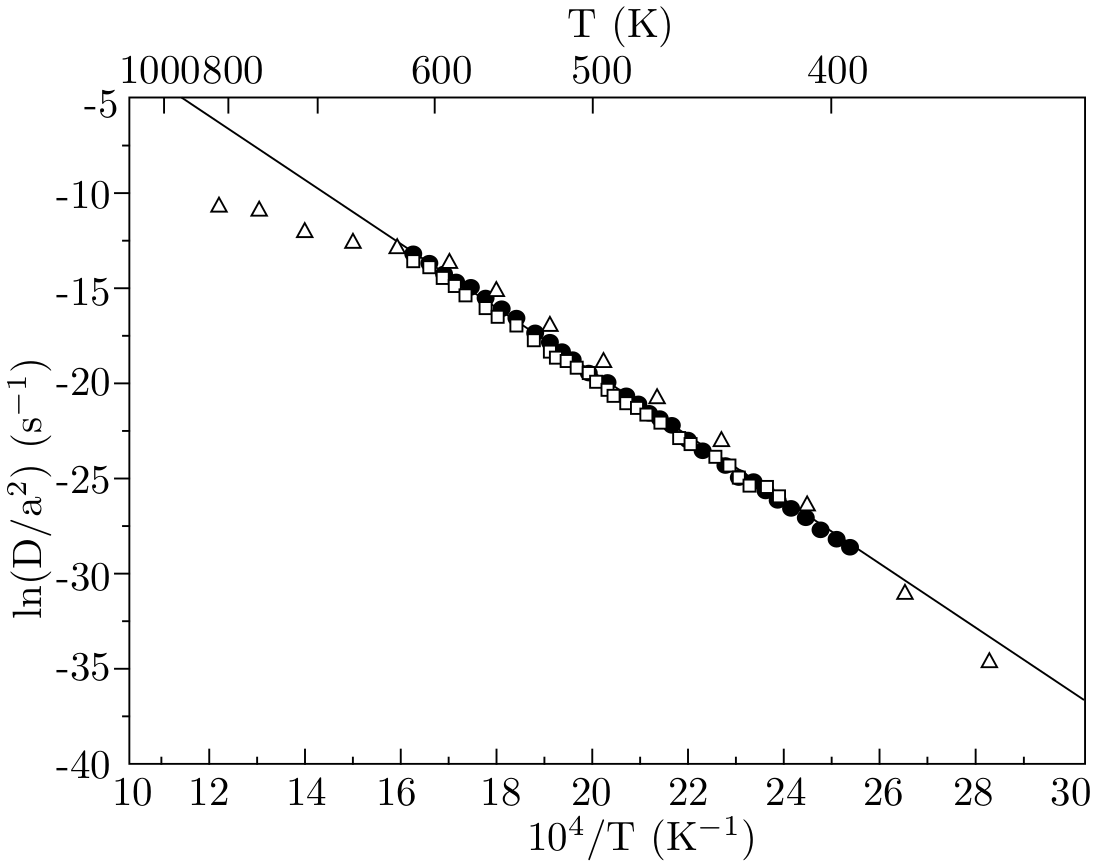
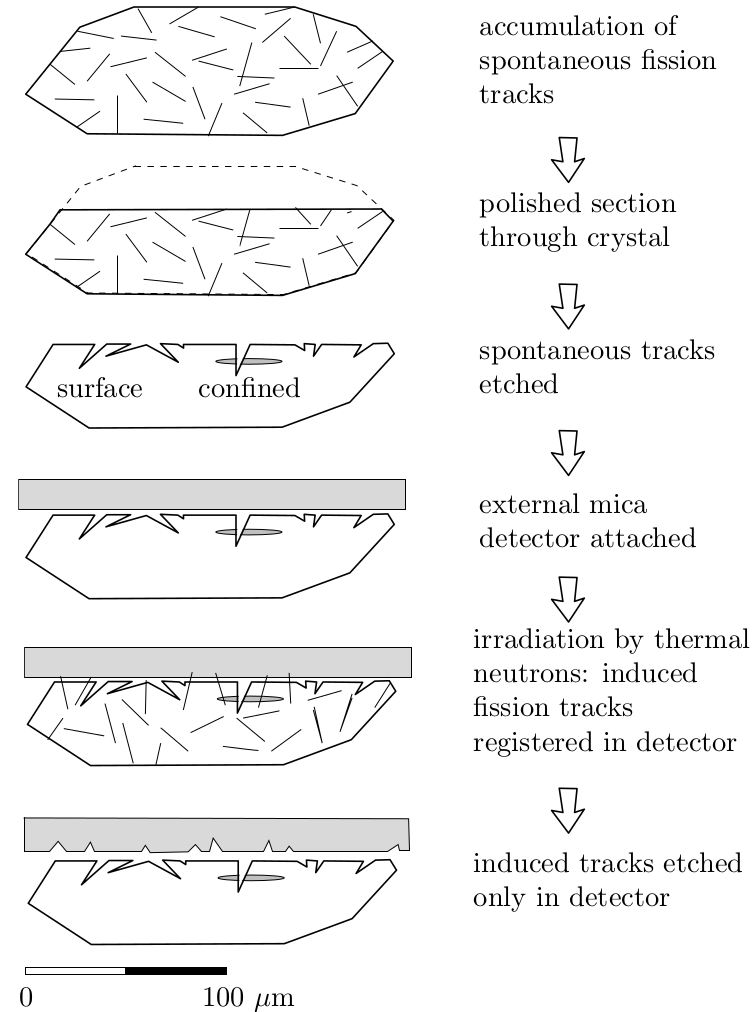
In addition to α, β and γ decay, which form the basis of the U-Th-Pb (Section 5) and U-Th-He (Section 7.1) methods, a tiny fraction (1/1,000,000) of the 238U atoms decay by spontaneous fission (Section 2.2). In this decay mechanism, the parent nuclide (i.e., 238U) decays into two daughter nuclides of roughly equal mass (e.g., Ba and Kr). These two particles carry a large amount of energy (~ 170 MeV) and, having a positive charge, strongly repel each other. Each of the two fission fragments travels through the crystal lattice of the host mineral, leaving a trail of damage behind. Although fission tracks can be directly observed by transmission electron microscopy (TEM), a more practical approach is to etch (a polished surface of) the host mineral with acid. This enlarges the damage zones and makes it possible to count them under an ordinary petrographic microscope. The volume density ns (in cm-3) of the fission tracks is given by:

λ](index69x.png) | (7.6) |
where [238U] stands for the volume density the 238U atoms, λf is the fission decay constant (8.46×10-17yr-1) and λ is the total decay constant of 238U (1.55125×10-10yr-1, see Section 5). The (unobservable) volume density of the tracks is related to the (observable) surface density ρs (in cm-2) by:
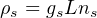 | (7.7) |
Where gs is geometry factor (gs=1 if determined on an internal and gs=1/2 on an external surface) and L is the etchable length of a fission track (~15μm). Rearranging Equation 7.6 for time:
![( )
t =-1ln λ----ρs--- + 1
λ λf[238U ]gsL](index71x.png) | (7.8) |
In practice, [238U] is determined by irradiating the (etched) sample with thermal neutrons in a reactor. This irradiation induces synthetic fission of 235U in the mineral (Equation 2.1). These tracks can be monitored by attaching a mica detector to the polished mineral surface and etching this monitor subsequent to irradiation (Figure 7.2). The surface density of the induced tracks in the mica detector (ρi) is a function of the nuclear cross section of the neutron-induced fission reaction on 235U and the neutron fluence in the reactor, both of which are unknown. A pragmatic solution to this problem is found by irradiating the sample along with a standard of known age, and lumping all the unknown parameters together into a calibration factor (ζ), so that the age of the sample reduces to:
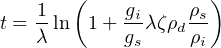 | (7.9) |
where gs = 1, gi = 1/2 and ρd is the surface density of the induced
fission tracks in a dosimeter glass of known (and constant) U concentration.
The latter value is needed to ‘recycle’ the ζ value from one irradiation batch
to the next, as neutron fluences might vary through time, or within a
sample stack.
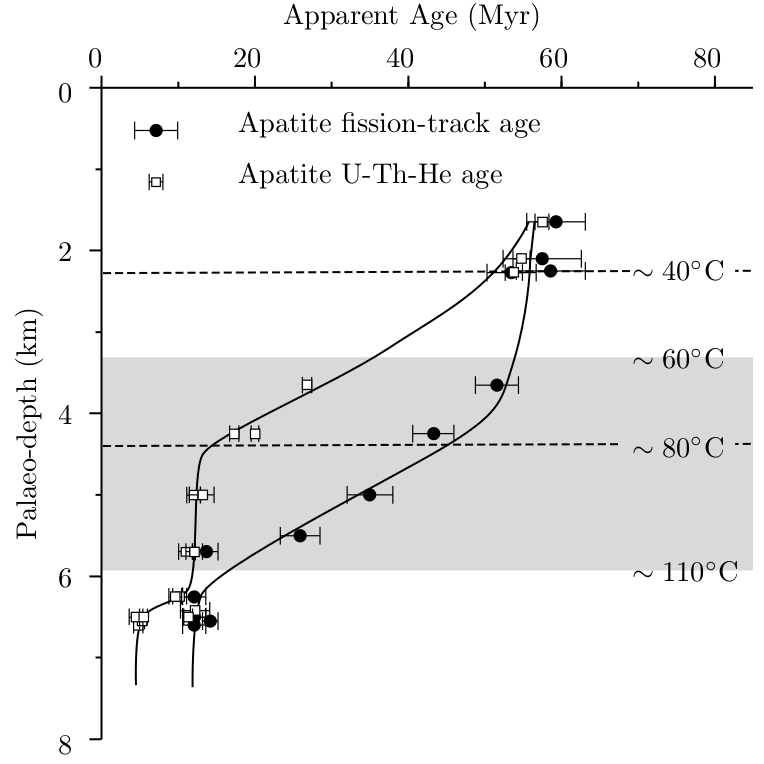
Laboratory experiments have revealed that fission tracks are sensitive to heat. For example, it suffices that apatite is heated to 500∘C for 1 hour for all the latent fission tracks to anneal. Moderate heating shortens the tracks and reduces their surface density and, hence, the apparent age of the sample. In boreholes, the apparent fission track age remains constant until a depth is reached where the ambient temperature is high enough for the tracks to be reduced in size and number. This region is called the Partial Annealing Zone (PAZ). Below the PAZ, no tracks are retained (Figure 7.3). The reduction of the surface density of the spontaneous tracks per unit time can be written as a function of temperature (T, in Kelvin):
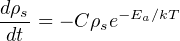 | (7.10) |
where C is a material constant, Ea is the activation energy for track shortening and k is the Boltzmann constant (8.616×10-5eV/K). Integration of Equation 7.10 yields:
 | (7.11) |
where ρ∘ is the initial track density prior to heating. Taking logarithms:
![EA [ (ρ∘ )]
ln(t) = kT-+ ln ln -ρ - ln(C)](index75x.png) | (7.12) |
For any given retention coefficient ρ∘∕ρ, there exists a linear relationship
between ln(t) and 1/T. This is an Arrhenius trend similar to the one
described by Equation 7.3 in the context of U-Th-He thermochronology. By
extrapolating the Arrhenius diagram to long time scales (t ~ 106yr), it is
possible to calculate a ‘closure temperature’ Tc similar to that which is
calculated for the U-Th-He system. For apatite, Tc ≈ 100∘C, whereas for
zircon, Tc ≈ 240∘C.
If a sample has spent some of its time inside the PAZ, then the subpopulation of its fission tracks formed during that thime will be shorter than those that subsequently formed above the PAZ. The probability distribution of the fission track lengths can be determined by measuring the distance between the two tips of a large number of (100, say) horizontally confined fission tracks under the optical microscope. Sophisticated inverse modelling algorithms have been developed to interpret these length distributions and extract continuous time-temperature (t-T) paths from them. Such modelling exercises have become an integral part of modern fission track studies.