Chapter 5
The U-Pb system

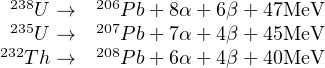
U and Th are found on the extremely heavy end of the Periodic Table of Elements. All their isotopes are radioactive and exhibit α-decay and sometimes even spontaneous fission (see Section 7.2). ²³²Th, ²³⁵U and ²³⁸U each form the start of long decay series comprising multiple α- and β emissions which eventually produce various isotopes of Pb:

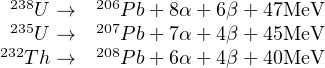(5.1)

Each of these three decay series is unique, i.e. no isotope occurs in more than one series (Figure 2.2). Furthermore, the half life of the parent isotope is much longer than any of the intermediary daughter isotopes, thus fulfilling the requirements for secular equilibrium (Section 2.4). We can therefore assume that the ²⁰⁶Pb is directly formed by the ²³⁸U, the ²⁰⁷Pb from the ²³⁵U and the ²⁰⁸Pb from the ²³²Th. Several chronometers are based on the α-decay of U and Th:

• The U-Th-Pb method (Section 5.1)
• The Pb-Pb method (Section 5.2)
• The U-Th-He method (Section 7.1)

5.1 The U-(Th-)Pb method

Natural Pb consists of four isotopes ²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb and ²⁰⁸Pb. The ingrowth equations for the three radiogenic Pb isotopes are given by:

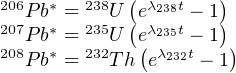(5.2)

With λ₂₃₈ = 1.55125 ×10^-10a^-1 (t_1∕2 = 4.468 Gyr), λ₂₃₅ = 9.8485 ×10^-10a^-1 (t_1∕2 = 703.8 Myr), and λ₂₃₂ = 0.495 ×10^-10a^-1 (t_1∕2 = 14.05 Gyr). The corresponding age equations are:

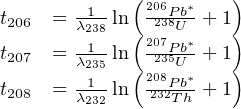(5.3)

Some igneous minerals (notably zircon) conveniently incorporate lots of U and virtually no Pb upon crystallisation. For those minerals, the non-radiogenic Pb can be safely neglected (at least for relatively young ages), so that we can assume that Pb ≈ Pb^*. This assumption cannot be made for other minerals, young ages, and high precision geochronology. In those cases, the inherited component (aka ‘common Pb’) needs to be quantified, which is done by normalising to non-radiogenic ²⁰⁴Pb:

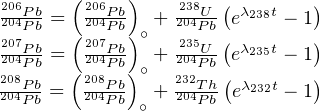(5.4)

where 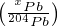_∘ stands for the common Pb component for isotope x. The corresponding age equations then become:

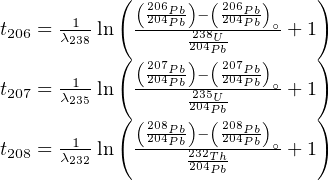(5.5)

U-Pb dating grants access to two separate geochronometers (²⁰⁶Pb/²³⁸U and ²⁰⁷Pb/²³⁵U) based on different isotopes of the same parent-daughter pair (i.e. U & Pb). This built-in redundancy provides a powerful internal quality check which makes the method arguably the most robust and reliable dating technique in the geological toolbox. The initial Pb composition can either be determined by analysing the Pb composition of a U-poor mineral (e.g., galena or feldspar) or by applying the isochron method to samples with different U and Th concentrations. As is the case for any isotopic system, the system needs to remain ‘closed’ in order to yield meaningful isotopic ages. This sometimes is not the case, resulting in a loss of Pb and/or U. Such losses cause the ²⁰⁶Pb/²³⁸U- and ²⁰⁷Pb/²³⁵U-clocks to yield different ages. Note that isotopic closure is required for all intermediary isotopes as well. Critical isotopes are the highly volatile ²²⁶Rn (t_1∕2=1.6ka) and ²²²Rn (t_1∕2=3.8d). Initially, the U-Pb method was applied to U-ores, but nowadays it is predominantly applied to accessory minerals such zircon and, to a lesser extent, apatite, monazite and allanite.

5.2 The Pb-Pb method

The ²⁰⁷Pb/²⁰⁶Pb method is based on the U-Pb method and is obtained by dividing the two U-Pb members of Equation 5.2 (or 5.4), and taking into account that the average natural ²³⁸U/²³⁵U-ratio is 137.818:

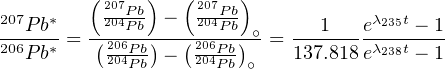(5.6)

The left hand side of this equation contains only Pb isotopic ratios. Note that these are only a function of time. Equations 5.6 has no direct solution and must be solved iteratively. The Pb-Pb method has the following advantages over conventional U-Pb dating:

• There is no need to measure uranium.
• The method is insensitive to recent loss of U and even Pb, because this would not affect the isotopic ratio of the Pb.

In practice, the Pb-Pb method is rarely applied by itself but is generally combined with the U-Pb technique. The expected (²⁰⁷Pb∕²⁰⁶Pb)^*-ratio for recently formed rocks and minerals can be calculated from Equation 5.6 by setting t→0:

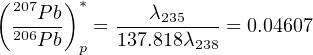(5.7)

This ratio was progressively higher as one goes back further in time. It was ≈ 0.6 during the formation of Earth.

5.3 Concordia

It sometimes happens that the U-Th-Pb trio of chronometers does not yield mutually consistent ages. It is then generally found that t₂₀₈ < t₂₀₆ < t₂₀₇ < t_207∕206 which, again, shows that the Pb-Pb clock is least sensitive to open system behaviour. From Equation 5.2, we find that:

(5.8)

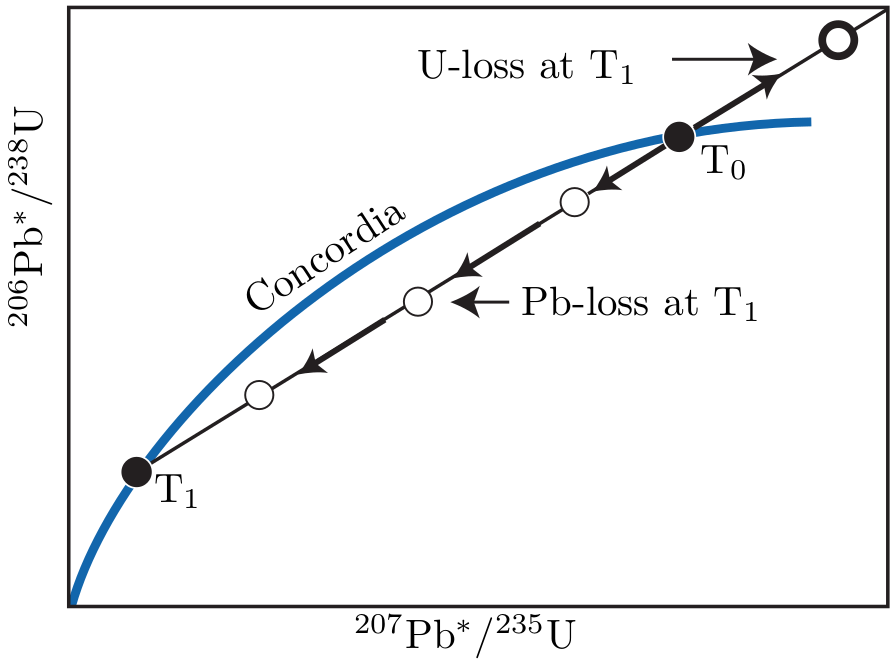
If we plot those ²⁰⁶Pb^*/²³⁸U- and ²⁰⁷Pb^*/²³⁵U-ratios which yield the same ages (t) against one another, they form a so-called ‘concordia’ curve. The concordia diagram is a very useful tool for investigating and interpreting disruptions of the U-Pb system caused by ‘episodic lead loss’. This means that a mineral (of age T_∘, say) has lost a certain percentage of its radiogenic Pb at a time T₁ after its formation (e.g., during metamorphism), after which the system closes again and further accumulation of radiogenic Pb proceeds normally until the present. On the concordia diagram of multiple aliquots of a sample, this scenario will manifest itself as a linear array of datapoints connecting the concordant ²⁰⁶Pb^*/²³⁸U - ²⁰⁷Pb^*/²³⁵U composition expected at T_∘ with that expected at T₁. With time, the data shift further away from the origin. The upper intercept of the linear array (aka discordia line) can be used to estimate the crystallisation age, whereas the lower intercept yields the age of metamorphism. The greater the distance from the expected composition at t, the greater the degree of Pb loss and the greater the linear extrapolation error on the crystallisation age (Figure 5.1).

5.4 Detrital geochronology

Zircon (ZrSiO₄) is a common U-Th-bearing accessory mineral in acidic igneous rocks, which form the main proto-sources of the siliciclastic sediments. Zircon is a very durable mineral that undergoes minimal chemical alteration or mechanical abrasion. Therefore, zircon crystals can be considered time capsules carrying the igneous and metamorphic history of their proto-sources. The probability distribution of a representative sample of zircon U-Pb ages from a detrital population can serve as a characteristic fingerprint that may be used to trace the flow of sand through sediment routing systems. As a provenance tracer, zircon U-Pb data are less susceptible to winnowing effects than conventional petrographic techniques. Using modern microprobe technology (SIMS and LA-ICP-MS, see Chapter 3.1), it is quite easy to date, say, a hundred grains of zircon in a matter of just a few hours. Due to the robustness of zircons as a tracer of sedimentary provenance, and the relative ease of dating them, the use of detrital zircon U-Pb geochronology has truly exploded in recent years. A literature survey using the keywords ‘detrital’, ‘zircon’, and ‘provenance’ indicates that the proliferation of detrital zircon studies has followed an exponential trend, with the number of publications doubling roughly every five years over the past two decades. At present, nearly a thousand detrital zircon publications appear each year.

An extensive survey of late Archaean sandstones from the Jack Hills in Australia have revealed a subpopulation of detrital zircons with Hadean (4.1-4.2 Ga) U-Pb ages. These are the oldest terrestrial minerals known to science, predating the oldest igneous rocks by 300 million years. The isotopic composition of oxygen, hafnium and other elements in the zircon represents a unique window into the earliest stages of Earth evolution. They indicate that liquid water was present on the surface of our planet early on in its history. This isotopic evidence is corroborated by the geological observation that the Hadean zircons are preserved in fluvial deposits.