Chapter 4
Simple parent-daughter pairs

4.1 ¹⁴C dating

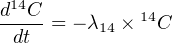
There are two stable isotopes of carbon: ¹²C and ¹³C, and one naturally occurring radionuclide: ¹⁴C. The half life of ¹⁴C is only 5,730 years, which is orders of magnitude shorter than the age of the Earth. Therefore, no primordial radiocarbon remains and all ¹⁴C is cosmogenic (see Section 8 for related methods). The main production mechanism is through secondary cosmic ray neutron reactions with ¹⁴N in the stratosphere: ₇¹⁴N (n,p) ₆¹⁴C. Any newly formed ¹⁴C rapidly mixes with the rest of the atmosphere creating a spatially uniform carbon composition, which is incorporated into plants and the animals that eat them. Prior to the industrial revolution, a gram of fresh organic carbon underwent 13.56 (β^-) decays per minute. When a plant dies, it ceases to exchange carbon with the atmosphere and the ¹⁴C concentration decays with time according to Equation 2.2:

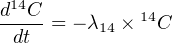(4.1)

where λ₁₄ = 0.120968 ka^-1. Thus, the radiocarbon concentration is directly proportional to the radioactivity, which can be measured by β-counting. This can then be used to calculate the radiocarbon age by rearranging Equation 2.3:

(4.2)

where (d¹⁴C∕dt)_∘ is the original level of β activity. This method was developed by Willard Libby in 1949, for which he was awarded the Nobel Prize in 1960. As mentioned before, (d¹⁴C∕dt)_∘ was 13.56 prior to the industrial revolution, when thousands of tonnes of ‘old’ carbon were injected into the atmosphere, resulting in a gradual lowering of the radiocarbon concentration until 1950, when nuclear testing produced an opposite effect, leading to a doubling of the atmospheric ¹⁴C activity in 1963. Since the banning of atmospheric nuclear testing, radiocarbon concentrations have steadily dropped until today, where they have almost fallen back to their pre-industrial levels. But even prior to these anthropogenic effects, ¹⁴C concentrations underwent relatively large fluctuations as a result of secular variations of the Earth’s magnetic field and, to a lesser extent, Solar activity. These variations in (d¹⁴C∕dt)_∘ can be corrected by comparison with a precisely calibrated production rate curve, which was constructed by measuring the ¹⁴C activity of tree rings (dendrochronology).

Since the 1980’s, β-counting has been largely replaced by accelerator mass spectrometry (AMS, see Section 3.1), in which the ¹⁴C concentration is measured directly relative to a stable isotope such as ¹³C. Although this has not significantly pushed back the age range of the radiocarbon method, it has nevertheless revolutionised the technique by reducing the sample size requirements by orders of magnitude. It is now possible to analyse individual seeds or tiny fragments of precious objects such as the Turin Shroud, which was dated at AD1260-1390.

4.2 The Rb-Sr method

Trace amounts of Rb and Sr are found in most minerals as substitutions for major elements with similar chemical properties. Rb is an alkali metal that forms single valent positive ions with an ionic radius of 1.48 Å, which is similar to K⁺ (1.33 Å). Rb is therefore frequently found in K-bearing minerals such as micas, K-feldspar and certain clay minerals. Strongly evolved alkalic rocks such as syenites, trachites and rhyolites often contain high Rb concentrations. Rb contains two isotopes of constant abundance: ⁸⁵Rb (72.1854%) and ⁸⁷Rb (27.8346%). Sr is an alkaline earth metal that forms bivalent positive ions with a radius of 1.13 Å, similar to Ca²⁺ (ionic radius 0.99 Å). It therefore substitutes Ca²⁺ in many minerals such as plagioclase, apatite, gypsum and calcite in sites with 8 neighbours, but not in pyroxene where Ca²⁺ has a coordination number of 6. Native Sr²⁺ can also substitute K⁺ in feldspars (where radiogenic Sr is expected to be found), but this substitution is limited and requires the simultaneous replacement of Si⁴⁺ by Al³⁺ in order to preserve electric neutrality. Sr therefore predominantly occurs in Ca-rich undifferentiated rocks such as basalts. Sr contains four isotopes (⁸⁴Sr, ⁸⁶Sr, ⁸⁷Sr and ⁸⁸Sr) with variable abundance due to the variable amount of radiogenic ⁸⁷Sr. However, the non-radiogenic ⁸⁴Sr/⁸⁶Sr and ⁸⁶Sr/⁸⁸Sr-ratios are constant with values of 0.056584 and 0.1194, respectively. The Rb-Sr chronometer is based on the radioactive decay of ⁸⁷Rb to ⁸⁷Sr:

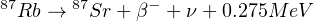(4.3)

Where ν indicates an antineutrino. The number of radiogenic ⁸⁷Sr atoms produced by this reaction after a time t is given by:

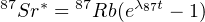(4.4)

where ⁸⁷Rb is the actual number of ⁸⁷Rb atoms per unit weight and λ₈₇ is the decay constant 1.42 × 10^-11 a^-1 (t_1∕2 = 4.88×10¹⁰a). In addition to this radiogenic ⁸⁷Sr, most samples will also contain some ‘ordinary’ Sr. The total number of ⁸⁷Sr atoms measured is therefore given by:

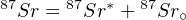(4.5)

with ⁸⁷Sr_∘ the initial ⁸⁷Sr present at the time of isotopic closure. Combining Equations 4.5 and 4.3, we obtain:

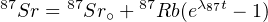(4.6)

Dividing this by the non-radiogenic ⁸⁶Sr yields

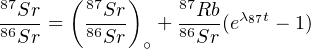(4.7)

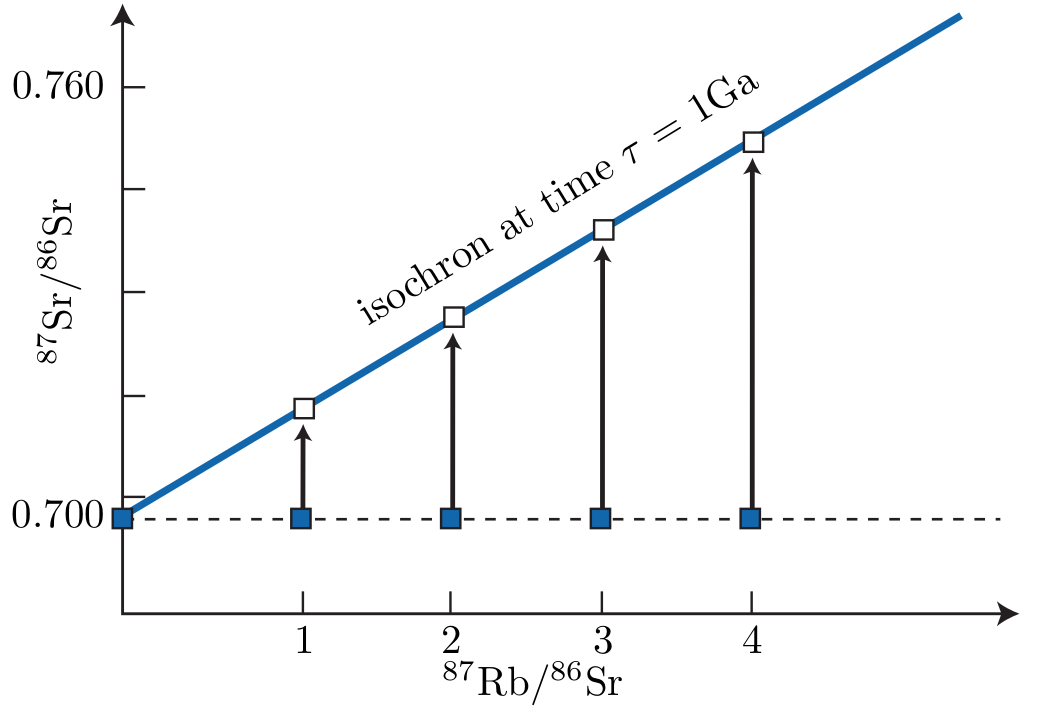
The method can be applied to single minerals or to whole rocks. Given the very long half life, the optimal time scale ranges from the formation of the solar system to the late Palaeozoic (300-400 Ma). To measure a Rb/Sr age, the weight percentage of Rb is measured by means of X-ray fluorescence, ICP-OES or similar techniques, and the ⁸⁷Sr/⁸⁶Sr ratio is determined by mass spectrometry (isotope dilution). The ⁸⁷Rb/⁸⁶Sr-ratio is then calculated as:

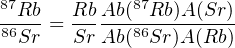(4.8)

Where Ab(⋅) signifies ‘abundance’ and A(⋅) ‘atomic weight’.

4.3 Isochrons

Equation 4.8 can be used in one of two ways. A first method is to use an assumed value for (⁸⁷Sr∕⁸⁶Sr)_∘, based on the geological context of the sample. This method is only reliable for samples with a high Rb/Sr ratio (e.g., biotite) because in that case, a wrong value for (⁸⁷Sr∕⁸⁶Sr)_∘ has only a minor effect on the age. A second and much better method is to analyse several minerals of the same sample and plot them on a (⁸⁷Rb∕⁸⁶Sr) vs. (⁸⁷Sr∕⁸⁶Sr) diagram (Figure 4.1). Due to Equation 4.7, this should form a linear array (the so-called isochron) with slope (e^λ₈₇t - 1) and intercept (⁸⁷Sr∕⁸⁶Sr)_∘. Both parameters can be determined by linear regression, allowing us to quantify the ‘goodness of fit’ of the data and obviating the need to assume any initial Sr-ratios.

4.4 The Sm-Nd method

The elements Neodymium (Z=60) and Samarium (Z=62) are so-called ‘rare earth elements’. All elements of this family have similar chemical properties. They nearly all form 3+ ions of roughly equal albeit slightly decreasing size with atomic number. The ionic radius of Nd and Sm is 1.08 and 1.04 Å, respectively. As the name suggests, rare earth elements rarely form the major constituents of minerals. One notable exception is monazite, which is a rare earth phosphate. In most cases, the rare earth elements are found in trace amounts of up to 0.1% in apatite [Ca₅(PO₄)₃(OH,Cl,F)] and zircon [ZrSiO₄]. Both Sm and Nd are slightly enriched in feldspar, biotite and apatite and thus tend to be found in higher concentrations in differentiated (alkalic) magmatic rocks.

Because their chemical properties are so similar, geological processes are rarely capable of fractionating the Sm and Nd concentrations. Therefore, the Sm/Nd ratio in most rocks generally falls in a narrow range of 0.1 to 0.5 (the Sm/Nd ratio of the solar system being 0.31). One exception is garnet, in which Sm/Nd ratios > 1 have been found. Partial melting of mafic minerals such as pyroxene and olivine produces lower Sm/Nd ratios in the fluid phase than the solid residue. The Sm/Nd ratio of magmatic rocks therefore decreases with increasing differentiation.

Natural Sm contains seven naturally occurring isotopes, three of which are radioactive (¹⁴⁷Sm, ¹⁴⁸Sm and ¹⁴⁹Sm). Only ¹⁴⁷Sm has a sufficiently short half life to be useful for geochronology. Nd also contains seven isotopes, of which only one is radioactive (¹⁴⁴Nd) but with a very long half life. ¹⁴³Nd is the radiogenic daughter of ¹⁴⁷Sm and is formed by α-decay. This forms the basis of the Sm-Nd chronometer. Analogous to the Rb-Sr method (Equation 4.4), we can write:

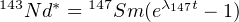(4.9)

Hence:

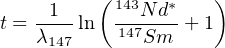(4.10)

With λ₁₄₇ = 6.54×10^-12a^-1 (t_1∕2 = 1.06×10¹¹a). Since most samples contain some initial Nd, the preferred way to calculate Sm/Nd ages is by analysing several minerals in a rock and create an isochron, similar to the Rb/Sr method (Section 4.3):

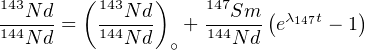(4.11)

All measurements are done by mass spectrometry using isotope dilution. Because of the identical atomic masses of ¹⁴⁷Sm and ¹⁴⁷Nd, it is necessary to perform a chemical separation between Sm and Nd prior to analysis.

The Sm/Nd method is generally applied to basic and ultrabasic igneous rocks (basalt, peridotite, komatiite) of Precambrian to Palaeozoic age. The method thus complements the Rb/Sr method, which is preferentially applied to acidic rock types. The Sm/Nd method can also be applied to high grade metamorphic rocks (granulites, eclogites) as well as meteorites (shergottites, nahklites). Since the rare earths are significantly less mobile than Rb and Sr, the Sm/Nd is more reliable in rocks that have been disturbed by weathering or metamorphism.