Statistical Mechanics & Soft Matter

Prof Ian Ford

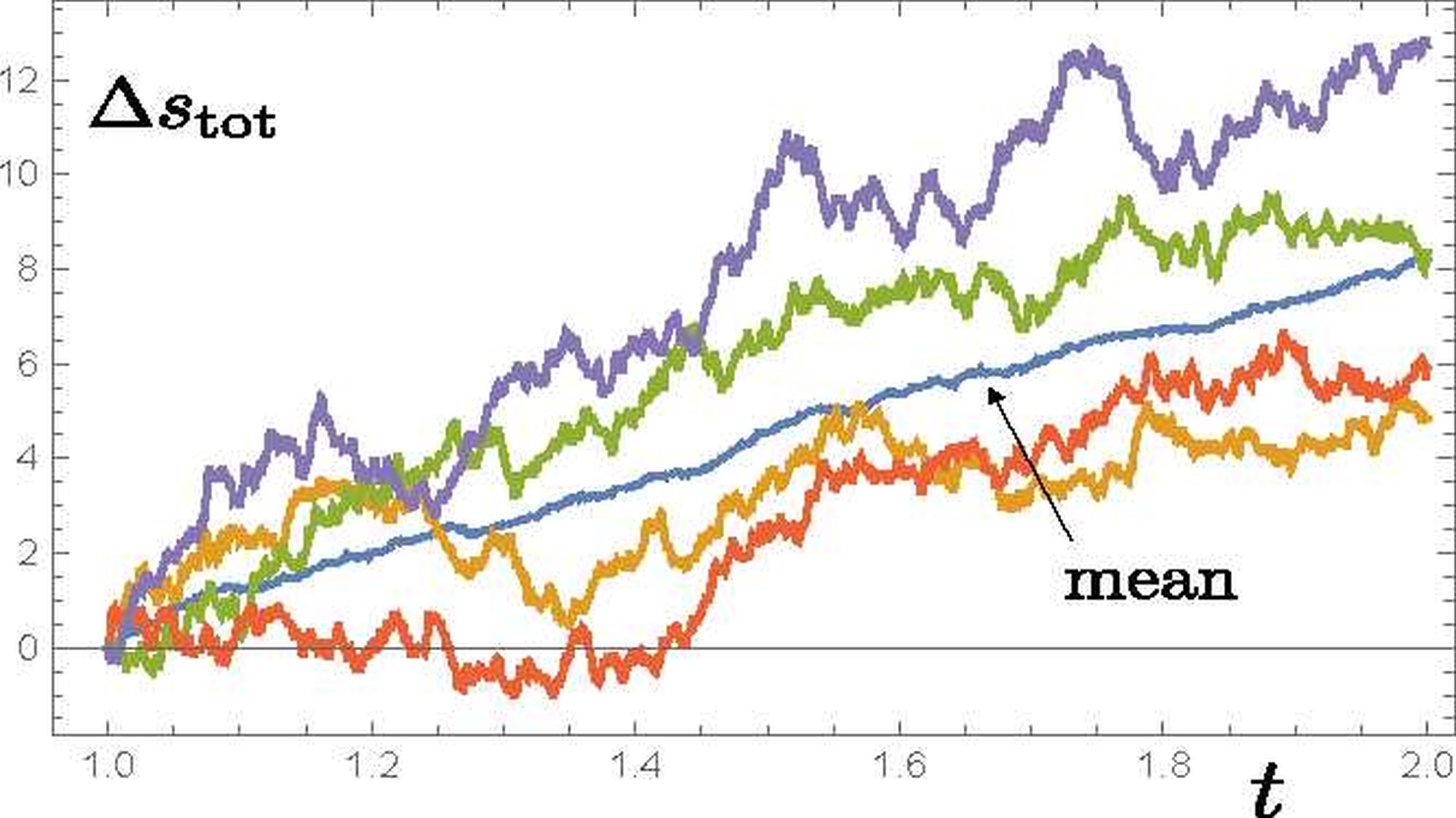
My research concerns the behaviour of systems out of equilibrium, such as phase transitions in molecular matter (for example water condensation, macromolecular structural selection, growth of crystalline materials), or quantum systems that are undergoing thermalisation or measurement. I am interested in the nature and meaning of entropy as a measure of the irreversibility of such transformations, and use statistical mechanics and stochastic thermodynamics to investigate various phenomena. The kinetics of crossing of thermodynamic barriers en route to equilibrium has been of particular interest, especially the nucleation of nanoparticles, such as aerosol formation from gaseous precursors.

Prof Edina Rosta

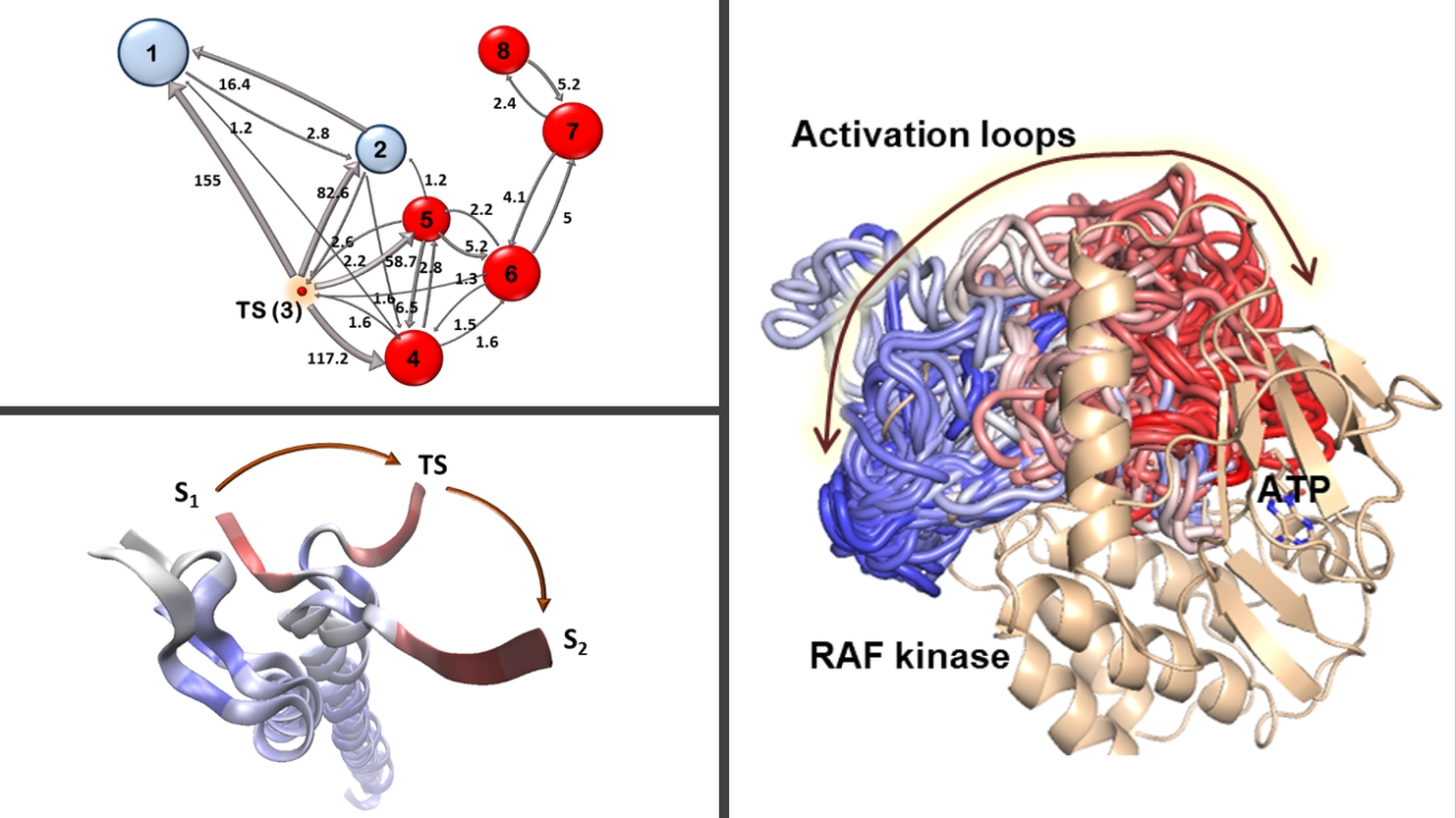
The Rosta research group focuses on how to enable computational design by understanding the catalytic power of enzymes using atomistic molecular modelling tools, including hybrid quantum mechanics/molecular mechanics (QM/MM) simulations. To quantitatively and accurately assess how enzymes achieve their extraordinary efficiency and specificity in performing chemical reactions, we develop and use modern enhanced sampling methods. Biased simulations are usually required to reach the relevant timescales of important biological processes using current simulation resources. We develop novel algorithms to calculate molecular kinetics in addition to free energies from biased molecular simulations using Markov chains defined on molecular conformational networks. Applications aim at understanding and molecular design concerning the most prominent chemical reactions of living organisms: phosphate transfer and cleavage.

Prof Marzena Szymanska

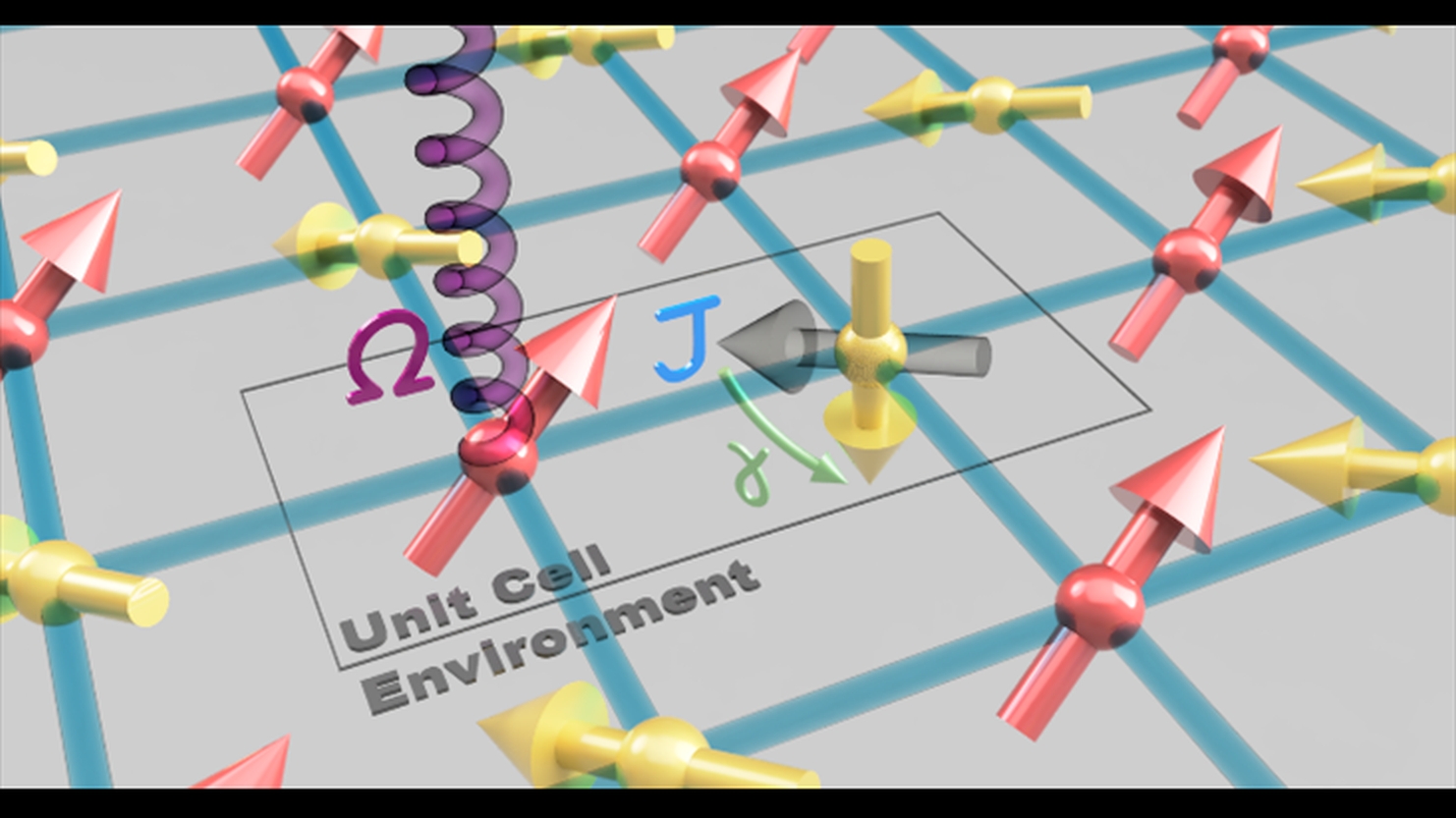
Our group researches out-of-equilibrium quantum phenomena in driven-dissipative light-matter systems. These systems bridge the gap between quantum optics and many-body quantum theory where many degrees-of-freedom give rise to emergent collective behaviour. The presence of drive and dissipation mean that the Hamiltonian is not the only source of dynamics, resulting in rich phenomena which is intrinsically different to its equilibrium counterpart. We apply a combination of analytical methods (Keldysh Field Theory, Renormalisation Group, Green’s Functions, Quantum Trajectories, Master Equations) in addition to numerical techniques (Stochastic Phase Space Simulations, Truncated Wigner,  Positive-P, Tensor Networks) to better understand novel behaviour in non-equilibrium, for example: superfluidity in condensates, phase transitions in low-dimensions and non-equilibrium universality classes such as Kardar-Parisi-Zhang (KPZ). Recently we have been extending our research to highly tuneable driven-dissipative lattices of bosons, spins and fermions. A large class of these can be faithfully represented by tensor networks and we are currently interested in extrapolating established ideas for closed systems to open systems to give insight into symmetry-protected phases and to address fundamental questions of entanglement growth.

Prof Neal Skipper

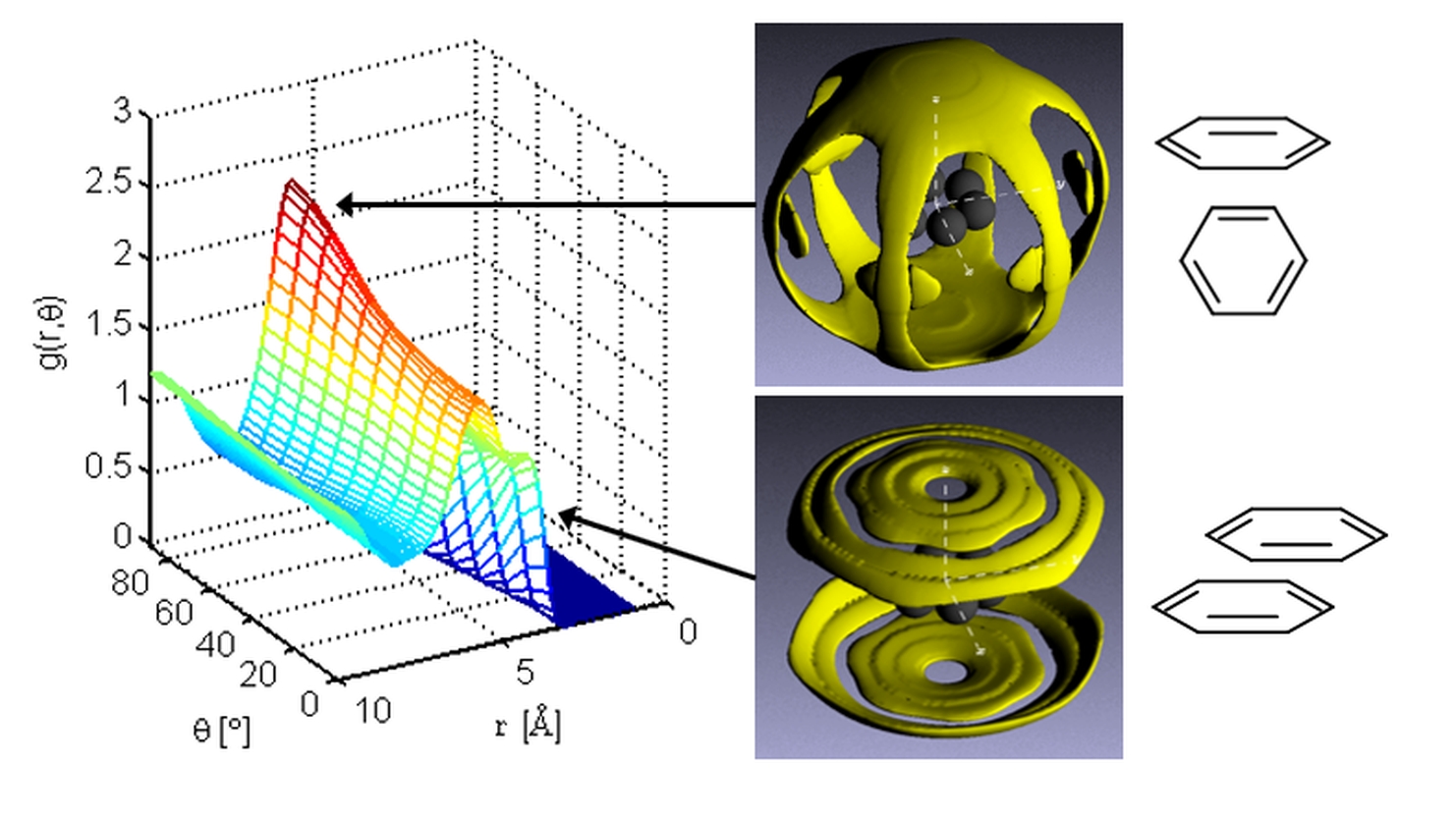
Our research aims to understand and control the properties of a wide range of functional materials, by building up a picture of where the atoms are what the atoms do. We are particularly interested in the behaviour of liquids and complex fluids, and are investigating their role as solvents and electrolytes along with the nature of the fundamental interactions that take place at interfaces and in nanoscale confinement. These interactions are a key factor in many important biological and chemical processes. We use a variety of experimental and computational techniques in our research. In addition to our laboratories at UCL, we also make extensive use of international neutron and X-ray scattering facilities. For example the ISIS Neutron Source at the STFC Rutherford Appleton Laboratory, and the Institute Laue-Langevin in Grenoble.

Prof Andrew G Green

My group has broad-ranging interest in many-body quantum phenomena. This encompasses novel phases of matter induced by quantum fluctuations, fundamental aspects collective quantum dynamics, and the development of new tools to address both. We are particularly interested in the interface between quantum field theory and tensor network techniques, and have pioneered the application of the latter to structure circuits for quantum simulation and quantum machine learning.