By Jem Hebden and Simon Arridge
Introduction
A diagnostic imaging modality based on near-infrared (NIR) radiation offers several potential advantages over existing radiological techniques. First, the radiation is non-ionizing, and therefore reasonable doses can be repeatedly employed without harm to the patient. Second, optical methods offer the potential to differentiate between soft tissues, due to their different absorption or scatter at NIR wavelengths, that are indistinguishable using other modalities. And third, specific absorption by natural chromophores (such as oxy-haemoglobin) allows functional information to be obtained. NIR imaging research has focused on a variety of possible clinical applications. Potentially the most important is the development of a means of screening for breast cancer, particularly if a specificity and sensitivity exceeding that of x-ray mammography can be achieved. Screening demands a spatial resolution of a few millimeters or better in order that tumours can be distinguished from surrounding healthy tissue while they are still small in size before metastasis occurs and treatment becomes more difficult. Another significant goal is to extend the success of NIR spectroscopy to develop a cerebral imaging modality for mapping structure and function in newborn infants, and possibly adults too. This application would not require such high spatial resolution as breast imaging, and 10 mm would probably be adequate. There is also interest high resolution imaging of thin or transparent tissues using a method known as Optical Coherence Tomography [1]. However, the discussion which follows is concerned with techniques where a potential to image through larger thicknesses of highly scattering tissues has been demonstrated, or at least claimed.
The first significant attempt at diagnostic imaging using optical radiation was made by Cutler [2], who transilluminated the female breast with a bright light source in a darkened room. However, even these early experiments revealed that the multiple scattering which occurs when light propagates through tissue causes features below the surface to appear extremely blurred. Despite attempts to improve breast transillumination by employing NIR sources and detectors, clinical trials have demonstrated that its clinical utility is severely limited [3].
The scatter coefficient µs of many soft tissues has been measured at a variety of optical wavelengths, and is typically within the range 10 - 100 mm-1 [4]. As a consequence, measurements of transmitted intensity through more than a few millimetres of tissue are dominated by scattered light, and imaging contrast is largely governed by photon interactions at the surface. The severity of scatter generally decreases with increasing wavelength, although the choice of wavelength is complicated by the need to consider the relative optical characteristics of the different tissues under investigation, the availability of suitable sources, and the sensitivity of the detector. The characteristic scatter of tissues is commonly expressed in terms of the transport scatter coefficient µs' = µs(1-g), where g is the mean cosine of the single scatter phase function. Typically µs' is about 1 mm-1 for breast and neonate brain tissues, but is larger for muscle and the adult brain. The other important fundamental characteristic of tissue is the absorption coefficient µa. Very strong absorption of red light by haemoglobin limits NIR studies to wavelengths to greater than about 600 nm, and significant water absorption prevents the use of wavelengths in excess of about 1 micron.
In general, researchers have approached the task of improving the performance of transillumination in two ways. The so-called direct approach is based on a reasonable assumption that photons which are least scattered provide inherently better spatial resolution and contrast since they propagate closest to a straight line through the tissue. Imaging therefore involves appropriate filtering, or "gating", to isolate this transmitted component from the majority of the multiply scattered light. A broad variety of gating techniques have been proposed and tested experimentally, many of which are described below. Some methods rely on a fraction of photons being able to propagate without scatter or loss of initial coherence or polarization state, while other methods gate according to the lengths of the photon paths. The second, indirect approach is based on the assumption that, given a set of measurements of transmitted light between pairs of points on the surface of an object, there exists a unique three-dimensional distribution of internal scatterers and absorbers which would yield that set. Thus imaging becomes a task of solving an inverse problem using an appropriate model of photon transport. In principle, the measurements could be of any type, even total transmitted intensity. However, the measurement of one or more characteristics of the temporal distribution of transmitted light, or an equivalent in the frequency domain, is considered more suitable. Mean photon flight time, for example, is found to be far less dependent on surface interactions than total transmitted intensity.
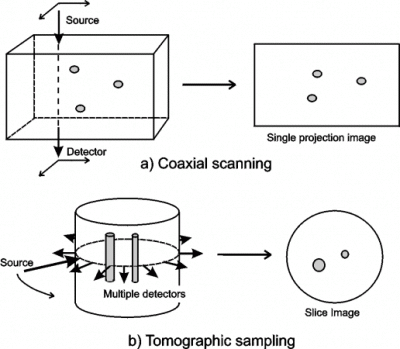
Figure 1: Potential data acquisition geometries for optical imaging of tissues. Many of the experimental systems used for optical imaging of tissues employ pencil beams of light and detectors with small sensitive areas. Therefore direct imaging often involves scanning the line-of-sight over a two-dimensional surface, as illustrated in figure 1(a). For optimum spatial resolution, coaxial scanning requires the detector area to be small, which results in the worse resolution occurring at the midplane between the entrance and exit surfaces [5]. Indirect methods generally involve detection at multiple sites for each source position. The most common sampling configuration is shown in figure 1(b), where detectors are arranged around the circumference of the tissue, and a source is moved to successive points around the same circumference. Whereas direct methods produce single projection images, indirect imaging enables slice images to be obtained. This approach has become known as optical tomography.
1. Collimated detection
In circumstances where the scatter of light within a medium is not too great, a collimator aligned co-axially with an incident beam of light can be employed effectively to isolate unscattered photons [6,7]. The gain in spatial resolution achieved by collimated detection is severely hindered by the detection of photons which are scattered back along the original line of sight. As the scatter occurring within the medium increases, the proportion of unscattered light decreases, and coaxial collimation no longer provides improvement in spatial resolution [5]. The maximum tissue thickness for which this approach is applicable is roughly given by:
d < (1 / µs) loge [Io / I] ,
where Io is the source intensity and I is the smallest detectable intensity. Even for the largest possible safe exposures and the most sensitive detectors, this limit corresponds to a thickness of just a few millimetres of human soft tissues. Not surprisingly, attempts to image through the breast using this method demonstrate very poor resolution and specificity [8]. An alternative implementation of the technique has been proposed by Wang et al [9] which employs a lens to produce the Fourier spectrum of the spatial distribution of light on the exit surface of a transilluminated object. By removing the high-order frequencies using a spatial filter, an image can be produced using only the light emitted at angles close to the normal to the exit surface of the object. However, this approach is subject to the same limitations as collimated detection.
2. Polarization discrimination
Photons which undergo a sufficiently large number of scatters will experience a complete randomization of their initial polarization state. However, it has been shown that in an anisotropically scattering medium, a significantly larger number of scatters are required to randomize the polarization of a circularly polarized wave than are required to randomize its direction of propagation [10]. The use of this fact to discriminate between short and long path photons in scattering media has been explored [11]. However, studies indicate that total depolarization is reached after a penetration depth equivalent to ten transport scattering mean free paths (equal to the reciprocal of the transport scatter coefficient), which again suggests that polarization discrimination will not be effective for imaging through more than about a centimetre of soft tissue [12].
3. Coherent gating
A broad variety of imaging methods have been investigated which involve attempting to exploit the fact that whereas unscattered photons retain coherence and phase, these properties are destroyed by multiple scattering. Coherent gating requires that the light transmitted through the turbid medium is combined spatially and temporally with a reference beam. Although the performance of the coherent methods described below differ in terms of gating efficiency and gate window length, they all require the existence of a transmitted coherent component.
3.1. Holographic gating
The first practical demonstration of so-called light-in-flight holography was presented by Abramson [13]. This technique involves illuminating an object with a short coherence length beam, and combining the reflected light with a reference beam delivered directly from the same source. The interference recorded on a photographic plate produces holographic images revealing two dimensional depth-dependent contours across the surface of the object. The shorter the coherence length of the source, the higher the depth resolution. This method has since become more generally known as holographic gating, and commonly employs short pulses to achieve the gating [14]. To produce interference, the reference pulse and the object pulse must coincide within the pulse duration, or within its coherence time if it is shorter. Schemes have been proposed for imaging through scattering media using various forms of holographic gating [15-18]. However, multiple scattering in tissue soon randomizes the phase of the electromagnetic vectors, and as thickness increases the coherent signal rapidly diminishes.
3.2. Heterodyne detection
An alternative means of isolating the coherent portion of transmitted light through tissue is that known as heterodyne detection. This involves recording the beat frequency generated when a beam of light is combined spatially and temporally with a frequency-modulated reference beam. Since only the coherent portion interferes with the reference beam, the isolated beat frequency has an amplitude proportional to its intensity. Heterodyne systems based on the Mach-Zehnder interferometer have been demonstrated by several investigators, and sensitivities in excess of 100 dB have been achieved [19-21]. This detection method has been widely used in optical coherence tomography [22], which is an effective tool for imaging thin or non-scattering tissues at the sub-millimetre scale.
3.3. Nonlinear techniques
A number of techniques have been developed which attempt to isolate unscattered or least-scattered light through tissue by exploiting various non-linear phenomena which occur when certain materials are illuminated by radiation at certain wavelengths. Some of these methods do not rely on the coherence of the detected signal, but require a source of short pulses. Alternatively, methods which require detection of a coherent signal can be implemented using continuous wave (CW) or long pulse sources. One such method is based on the nonlinear optical phenomenon known as coherent anti-Stokes Raman scattering (CARS). This involves the generation of a signal at a separate wavelength (anti-Stokes radiation) by coherent interference of two beams within a CARS cell [23]. A similar technique has been investigated which exploits an optical phenomenon known as resonant degenerate four wave mixing [24]. A signal produced by resonant atomic or molecular transitions within a dye cell carries information about the coherent interaction between a probe beam transmitted through a scattering medium and a reference beam. The signal is in the form of a phase conjugate of the probe beam, which facilitates its separation and detection without contamination by the incoherent component.
4. Ultrafast shuttering
The sub-nanosecond gating times which are required to isolate less scattered photons from the majority of light transmitted through thick turbid media eliminates the possibility of using mechanical shutters. However, certain non-linear optical phenomena can be exploited in order to sample the intensity of diffuse light over a short period of time of arbitrary length. Sampling is performed by modulating the intensity passing through the gate, either by amplifying the signal of interest (nonlinear amplifier) or attenuating the unwanted light (Kerr gate). The advantage these shuttering methods have over techniques described above is that the detection of unscattered or coherent light is no longer essential.
4.1. Kerr gate
Probably the first attempt at tissue imaging using ultrafast optical technology was reported in 1980 by Martin et al [25] who used a fast shutter consisting of a Kerr cell in which birefringence was induced using short infrared pulses. By locating the cell between crossed polarizers, the birefringence produces an increase in the overall transmission for the duration of the pulse. High resolution images through scattering media may be obtained by selectively sampling the transmitted photons with the shortest flight times [26]. Unfortunately, the performance of Kerr gate imaging techniques is ultimately limited by the dynamic range of the transmission opacity of the cell, which is typically no better than 10,000. Thus the shortest flight time photons cannot be sampled accurately when their number represent much less than a few percent of the total transmitted intensity. Therefore a centimetre or so of tissue would appear to be the maximum thickness for which Kerr gating would be an effective method of isolating shorter flight-time photons.
4.2. Raman amplifier
Researchers at the NRL in Washington have created a fast time gate using stimulated Raman scattering (SRS). This phenomenon can be exploited using either short laser pulses [27] or longer laser pulses with short coherence times [28]. SRS is a nonlinear Raman interaction that occurs in specific materials such as hydrogen gas, and involves the amplification of a long-wavelength (Stokes) beam by a shorter-wavelength pump beam. The difference between the wavelengths must be equal to a fundamental vibrational frequency of the material. The SRS system can be operated as a time gate by selectively amplifying only the earliest light transmitted through scattering media. The contrast in opacity of the SRS gate depends on the amplification, which can be as high as 106. As for the Kerr cell, the gating method does not rely on the coherent properties of the light, and the duration of the gate depends on the pulse length of the pump beam.
4.3. Second harmonic generation
An attempt to exploit second harmonic generation (SHG) to image through scattering media was first reported by Yoo et al [29]. Two beams of pulses are combined within a nonlinear crystal so that the light emitted at the SHG wavelength depends on the degree of spatial and temporal overlap. One beam is passed through the medium of interest, while the other acts as a reference via a variable delay. Although the beams need not be coherent, the effective aperture of a system is limited by the second-harmonic phase-matching acceptance angle. As a consequence, a beam of scattered photons will only combine with the reference beam to yield a second harmonic signal if they are almost exactly parallel. This gating method is also severely limited by the poor SHG conversion efficiency of nonlinear crystals. A three-dimensional SHG imaging technique has also reported [30].
4.4. Parametric amplifier
Another type of high-gain ultrafast amplifying gate has been investigated using a phenomenon known as optical parametric amplification (OPA) [31,32]. If light pulses transmitted through a scattering medium and a frequency-doubled reference pulse are combined spatially and temporally within a non-linear crystal, light will be emitted at frequencies equal to the sum and difference of the two beams. It has been suggested [31] that a potential advantage of this technique is the facility to image at longer NIR wavelengths at which tissues are less highly scattering while detecting the signal of interest at shorter wavelengths at which detectors are more efficient. As for the SHG method described above, the requirement for collinear phase-matching severely limits the angular selectivity of OPA. So far only unscattered light has been amplified in practice.
5. Streak camera
The temporal distribution of photons produced when a very short (few ps) pulse of light is transmitted through a highly scattering medium is generally known as the temporal point spread function (TPSF). This is illustrated in figure 2(a). For several centimetres of soft tissue, the TPSF will extend over several nanoseconds, and for safe exposures there is no realistic hope of detecting an unscattered, polarized, or coherent component. The ideal time gate detector is one which can sample transmitted photons over any temporal window without contamination by photons arriving outside the window. The device which comes nearest to this ideal is the optical streak camera. Streak cameras are able to record entire TPSFs along a single line-of-sight with a temporal resolution of a few picoseconds. The versatility of streak cameras has enabled many fundamental experiments to be performed to explore the potential and limitations of time-gated methods, with particular emphasis on the feasibility of breast imaging. The streak camera was first used by Ho et al [33] to detect hidden objects in scattering media (using reflected laser pulses), and later by Hebden et al [34,35] to generate the first two-dimensional time-gated images. The latter were obtained by integrating transmitted intensity over a variable interval delta-t following the time at which an unscattered photon would have been detected. Experiments have shown that, as expected, an increase in spatial resolution correlates with a decrease in minimum photon flight time [36].The principal disadvantages of streak cameras compared to other time-gate technologies are the high cost and relatively small effective light collection area.
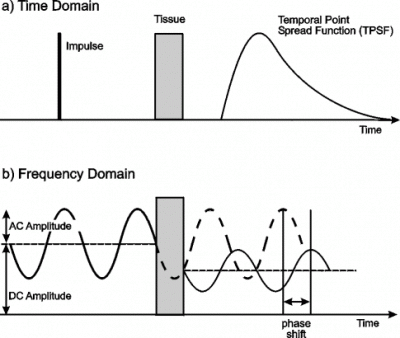
Figure 2: Time and frequency domain measurement of light through tissue.
6. TCSPC systems
An alternative technology for measuring entire TPSFs through large thicknesses of tissue is that based on Time Correlated Single Photon Counting (TCSPC). This involves using the output of photon-sensitive photo-multiplier-tube (PMT) to trigger an analog timing device, such as a time-to-amplitude converter (TAC). Several TAC-based systems have been developed for optical imaging through tissue [37-39]. The UCL 32-channel imager (MONSTIR) is based on another device, known as a time-to-digital converter [40]. Compared to the streak camera, TCSPC technology offers superior light collection efficiency at a substantially reduced cost. However, the photon count rate is limited by the state-of-the-art electronics (currently around 100,000 counts per second), and temporal resolution is limited by the transit time spread of PMTs or microchannel-plate PMTs (about 50 ps at best).
7. Other time domain technologies
Current trends in the development of ultrafast electronics suggest that increasingly fast and less expensive devices will continue to become available over the next few years. A relatively inexpensive device based on the avalanche photodiode detector (APD) has been investigated at UCL [41]. Click here for more details. Another novel time resolved measurement system is described by de Haller and Depeursinge [42] which consists of a very fast photodiode and a 50 GHz digitizing oscilloscope.
8. Frequency domain methods
Since any measurement in the time domain can be equivalently expressed in the frequency domain, techniques have also been developed which have sought to acquire transmitted light information in the frequency domain directly. As illustrated in figure 2(b) above, frequency domain techniques involve illuminating the object with an intensity-modulated beam, and measuring the AC modulation amplitude and phase shift of the transmitted signal, typically using a standard heterodyne method. The transport of the modulated beam is often described in terms of the propagation of so-called photon density waves. In principle, if a range of different frequencies are employed, the TPSF can be reconstructed with arbitrary precision. The principal advantage over time domain measurement is that continuous light sources and detectors can be employed which are generally less expensive. A significant disadvantage is that sources are not yet available that can provide significant power at very high frequencies. Most experimental work performed so far has utilized frequencies of a few hundred MHz, which is equivalent to a temporal resolution of a few nanoseconds, and photon density wavelengths of the order of a metre. The first frequency-domain measurements of photon migration in tissues was reported by Lakowicz and Berndt [43]. Since then, many research groups have demonstrated the effectiveness of frequency domain systems for tissue imaging [44-48], including the first in vivo images [45,46]. Some industrial companies have built breast imaging devices based on frequency domain measurement. Separate preliminary clinical trials have already been performed using prototypes at Carl Zeiss [49] and Siemens [50]. Philips Research Labs have also built a prototype imager, although currently it is based on straightforward intensity measurement [51].
References
- Fercher, AF (1996): J. Biomed. Opt. 1, 157-173.
- Cutler, M (1929): Surg. Gynecol. Obstet. 48, 721-728.
- Monsees, B, Destouet, J, and Gersell, D (1987): Radiology 163, 467-470.
- Cheong, W-F, Prahl, S, and Welch, AJ (1990): IEEE J. Quant. Electron 26, 2166-2185.
- Hebden, JC, and Kruger, RA (1990): Med. Phys. 17, 41-47.
- Jarry, G, Ghesquiere, S, Maarek, JM, Fraysse, F, Debray, S, Bui, M-H, and Laurent, D (1984): J. Biomed. Eng. 6, 70-74.
- Jackson, PC, Stevens, PH, Smith, JH, Kear, D, Key, H, and Wells, PNT (1987): Brit. J. Rad. 60, 375-380.
- Kaneko, M, et al (1989): Radiation Med. 7, 129-134.
- Wang, L, Ho, PP, and Alfano, RR (1993): Appl. Opt. 32, 5043-5048.
- MacKintosh, FC, Zhu, JX, Pine, DJ, and Weitz, DA (1989): Phys. Rev. B 40, 9342-9345.
- Schmitt, JM, Gandjbakhche, AH, and Bonner, RF (1992): Appl. Opt. 31, 6535-6546.
- Bruscaglioni, P, Zaccanti, G, and Wei, Q (1993): Appl. Opt. 32, 6142-6150.
- Abramson, NH (1978): Opt. Lett. 2, 121-123.
- Abramson, NH, and Spears, KG (1989): Appl. Opt. 28, 1834-1841.
- Spears, KG, Serafin, J, Abramson, NH, Zhu, X, and Bjelkhagen, H (1989): IEEE Trans. Biomed. Eng. 36, 1210-1221.
- Leith, E, Chen, H, Chen, Y, Dilworth, D, Lopez, J, Masri, R, Rudd, J, and Valdmanis, J (1991): Appl. Opt. 30, 4204-4210.
- Rebane, A, and Feinberg, J (1991): Nature 351, 378-380,
- Hyde, SCW, Parry, NP, Jones, R, Dainty, JC, French, PMW, Klein, MB, and Wechsler, BA (1995): Opt. Lett. 20, 1331-1333.
- Inaba, H, Toida, M, and Ichimua, T (1990): SPIE Proc. 1399, 108-115.
- Hee, MR, Izatt, JA, Swanson, EA, and Fujimoto, JG (1993): Opt. Lett. 18, 1107-1109.
- Schmidt, A, Corey, R, and Saulnier, P (1995): Opt. Lett. 20, 404-406.
- Huang, D, Swanson, EA, Lin, CP, Schuman, JS, Stinson, WG, Chang, W, Hee, MR, Flotte, T, Gregory, K, Puliafito, CA, and Fujimoto, JG (1991): Science 254, 1178-1181.
- Reintjes, J, Bashkansky, M, Duncan, MD, Mahon, R, Tankersley, LL, Moon, JA, Adler, CL, and Prewitt, JMS (1993): Opt. & Phot. News 4, 28-32.
- Sappey, AD (1994): Appl. Opt. 33, 8346-8354.
- Martin, JL, Lecarpentier, Y, Antonetti, A, and Grillon, G, (1980): Med. & Bio. Eng. & Comput. 18, 250-252,
- Wang, L, Ho, PP, Liu, C, Zhang, G, and Alfano, RR (1991): Science 253, 769-771.
- Mahon, R, Duncan, MD, Tankersley, LL, and Reintjes, J (1993): Appl. Opt. 32, 7425-7433.
- Bashkansky, M, and Reintjes, J (1993): Opt. Lett. 18, 2132-2134.
- Yoo, KM, Xing, Q, and Alfano, RR (1991): Opt. Lett. 16, 1019-1021.
- Yan, C, and Diels, J-C (1992): Appl. Opt. 32, 6869-6873.
- Faris, GW, and Banks, M (1994): Opt. Lett. 19, 1813-1815.
- Watson, J, Georges, P, Lépine, T, Alonzi, B, and Brun, A (1995): Opt. Lett. 20, 231-233.
- Ho, PP, Baldeck, P, Wong, KS, Yoo, KM, Lee, D, and Alfano, RR (1989): Appl. Opt.28, 2304-2310.
- Hebden, JC, Kruger, RA, and Wong, KS (1991): Appl. Opt. 30, 788-794.
- Hebden, JC, Hall, DJ, Firbank, M, and Delpy, DT (1995): Appl. Opt. 35, 8038-8047.
- Hebden, JC (1992): Med. Phys. 19, 1081-1087.
- Berg, R, Jarlman, O, and Svanberg, S (1993): Appl. Opt. 32, 574-579.
- Benaron, DA, and Stevenson, DK (1993): Science 259, 1463-1466.
- Charbonneau, S, Allard, LB, Young, JF, Dyck, G, and Kyle, BJ (1992): Rev. Sci. Instrum. 63, 5315-5319.
- Wells, K, Hebden, JC, Schmidt, FEW, and Delpy, DT (1997): Proc. SPIE 2979, 599-607.
- Kirkby, DR and Delpy, DT (1995): Proc. SPIE 2389, 190-197.
- de Haller, EB, and Depeursinge, C (1994): OSA Proc. 21, 88-92.
- Lakowicz, JR, and Berndt, K (1990): Chem. Phys. Lett. 166, 246-252.
- Sevick, EM, Lakowicz, JR, Szmacinski, H, Nowacyzk, K, and Johnson, ML (1992): J. Photochem. Photobiol. B: Biol. 16, 169-185.
- Gratton, E, Mantulin, WM, vandeVen, MJ, Fishkin, JB, Maris, MB, and Chance, B (1993): Bioimaging 1, 40-46.
- Maris, M, Gratton, E, Maier, J, Mantulin, W, and Chance, B (1994): Bioimaging 2, 174-183.
- O'Leary, MA, Boas DA, Chance, B, and Yodh, AG (1995): Opt. Lett. 20, 426-428.
- Pogue, BW, Patterson, MS, Jiang, H, and Paulsen, KD (1995): Phys. Med. Biol. 40, 1709-1729.
- Kaschke, M, Jess, H, Gaida, G, Kaltenbach, J-M, and Wrobel, W (1994): OSA Proc.21, 88-92.
- Mitic, G, Kölzer, J, Otto, J, Plies, E, Sölkner, G, and Zinth, W (1994): Appl. Opt. 33, 6699-6710.
- Papaioannou, DG, Colak, SB, and 't Hooft, GW (1995): Proc. SPIE 2626, 218-227.
Last update: January 26, 1999
 Close
Close


