Introduction
The TeraGyroid project was a three-month project funded by the EPSRC in the UK and the NSF in the USA, to join the UK e-Science Grid and the US TeraGrid. The main objective was to deliver scientific results which it would not be possible to obtain without the combined resources of the US and UK grids. The project features the world's largest lattice Boltzmann simulation of its kind, to study defect dynamics in liquid crystalline surfactant systems.
The TeraGyroid project won the "Most innovative data-intensive application" award at the Supercomputing 2003 conference, and the "Integrated Data and Information Management" award at the ISC2004 supercomputing conference.
Amphiphile mesophases
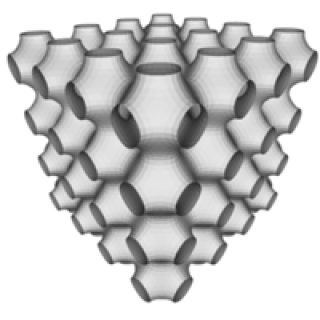 |  |  |
The P, D, and G surfaces.
Molecules in an ordinary liquid will usually have random orientations. There is a certain interesting class of liquids, called liquid crystals, in which this is not the case: the molecules exhibit a tendency to align or order. Liquid crystals have some of the properties of crystals, since they exhibit long-range ordering and strong anisotropy, but retain the ability to flow, unlike ordinary crystals in which the molecules are locked onto well-defined positions on a lattice.
Amphiphiles are one class of molecule which may produce liquid crystalline behaviour. These are molecules constructed from two parts, usually a water-loving head and a long tail which is attracted to oil. In a mixture of oil, water, and amphiphile, amphiphile molecules are attracted to the interface between the oil and water to minimize free energy, hence they are often termed ``surface active agents'', or surfactants. Their precise behaviour is strongly dependent on concentration, so they are termed ``lyotropic'' liquid crystals.
A random mixture of oil, water, and surfactant molecules will often spontaneously arrange itself into separate regions of oil and water, separated by a layer of surfactant at the interface, forming structures called surfactant mesophases. These structures can be very complex, and their geometry depends strongly upon the relative proportions of different molecules in the mixture, and the details of how they interact. Such structures can also be produced in binary systems, such as water-lipid mixtures, and often occur in biological systems [1][2][3] .
Surfactant mesophases will often form minimal surfaces: for any boundary drawn on the surface, the surface lying inside the boundary will have the minimal possible surface area, and the surface will also have zero mean curvature. Triply periodic minimal surfaces [4] which extend through space with cubic symmetry [5] have been found in many systems, such as lipid-water mixtures [1] , diblock copolymers [6] , and in many biological systems [7] .
As a Platonic or mathematical abstraction, the gyroid consists of perfect copies of the unit cell, repeating on a Bravais lattice extending through space. This is not the case for gyroid structures in the real world: various effects may give rise to regions where the structure deviates from a gyroid. Such deviations are called defects .
Defects in amphiphile mesophases
During the gyroid self-assembly process, several small, separated gyroid-phase regions or domains may start to form, and then grow. Since the domains evolve independently, the lattices describing them may not be identical, and can differ in orientation, position, or unit cell size. The interface between the domains will not be gyroidal: therefore, grain-boundary defects arise between gyroid domains. Inside a domain, there may be dislocations, or line defects, corresponding to the termination of a plane of unit cells; there may also be localised non-gyroid regions, corresponding to defects due to contamination or inhomogeneities in the initial conditions.

Volume rendering of a domain wall in a simulated gyroid mesophase. Oil is coloured red, water is blue, and the interface between the two, containing surfactant, is coloured green.
While equilibrium gyroid mesophases and their defects are observed experimentally, it is desirable to formulate a theoretical or computational model to better understand how and why they form and how they evolve.
Much effort has been invested in theoretical and computational modelling of liquid crystals. Nematic liquid crystals have been modelled using the Leslie-Erickson formulation [8] ; Monte Carlo [9][10] and Molecular Dynamics [11] simulations have provided some insight, but reaching regimes where hydrodynamic effects are significant is currently computationally unfeasible with these techniques.
Lyotropic liquid crystals, of interest in this paper, have also been studied extensively [12] through techniques such as free-energy methods [13][14] and through consideration of the interface between the lipid and water phases; again, most treatments have been limited to examination of the equilibrium state and its stability.
We used a lattice Boltzmann model, which employs a ``bottom-up'' approach to model interactions between particles [15][16] including surfactants [17] , postulating a form of interparticle potential rather than using a free-energy-based technique.
On a sufficiently small lattice, the gyroid may evolve to perfectly fill the simulated region, without defects. As the lattice size grows, it becomes more probable that multiple gyroid domains will emerge independently, so that grain boundary defects are more likely to appear and the time required for localized defects to diffuse across the lattice increases making it more likely that defects will persist. Therefore, examination of the defect behaviour of surfactant mesophases requires the simulation of very large systems. This was achieved as part of the TeraGyroid project, where systems on lattice sizes of up to 10243 were simulated by linking together multiple geographically-distributed supercomputing resources to form a computational Grid [18][19].
Images from TeraGyroid
We have been able to observe many hitherto unseen features of the gyroid evolution, and publications are in preparation. Below are some images generated from the TeraGyroid simulations.

Isosurface showing the oil-water interface on a 2563 simulation. The interface is coloured to show surfactant distribution, which is nonuniform, inducing currents which in turn lead to interface deformation.

Blob structures in a domain wall between two chiral gyroid domains.

A virtual transmission electron micrograph of a simulated gyroid mesophase with defects.
References
[1] J. M. Seddon , R. H. Templer , p 97--160(1995) Elsevier Science B. V.
[2] J. M. Seddon , R. H. Templer , Phil. Trans.: Phys. Sci. Eng. 344 p 377--401(1993)
[3] C. Czeslik , R. Winter , J. Mol. Liq. 98 p 283--291(2002)
[4] H. Karcher , K. Polthier , Phil. Trans. R. Soc. Lond. A 354 p 2077--2104(1996)
[5] E. A. Lord , A. L. Mackay , Cur. Sci. 85 p 346--362(2003) http://www.ias.ac.in/currsci/aug102003/346.pdf
[6] T. A. Shefelbine , M. E. Vigild , M. W. Matsen , D. A. Hajduk , M. A. Hillmyer , E. L. Cussler , F. S. Bates , J. Am. Chem. Soc. 121 p 8457--8465(1999)
[7] T. Landh , FEBS Lett. 369 p 13--17(1995) doi:10.1016/0014-5793(95)00660-2
[8] P. G. d. Gennes , J. Prost , (1995) Oxford University Press
[9] D. Frenkel , R. Eppenga , Phys. Rev. Lett. 79 p 1089--1092(1982)
[10] M. P. Allen , Mol. Phys. 96 p 1391--1397(1999) http://ariel.ingentaselect.com/vl=2206979/cl=90/nw=1/rpsv/cw/tandf/00268976/v96n9/s10/p1391 doi:10.1080/002689799164621
[11] M. P. Allen , M. A. Warren , Phys. Rev. E 57 p 5585--5596(1998) http://link.aps.org/abstract/PRE/v57/p5585 doi:10.1103/PhysRevE.57.5585
[12] G. Gompper , M. Schick , 16 p 1--176(1994) Academic Press
[13] A. Ciach , R. Ho\lyst , J. Comp. Phys. 110 p 3207--3214(1999)
[14] R. Ho\lyst , P. Oswald , J. Comp. Phys. 109 p 11051--11060(1998)
[15] X. Shan , H. Chen , Phys. Rev. E 47 p 1815--1819(1993) doi:10.1103/PhysRevE.47.1815
[16] N. S. Martys , J. F. Douglas , Phys. Rev. E 63 p 031205(2001) doi:10.1103/PhysRevE.63.031205
[17] H. Chen , B. M. Boghosian , P. V. Coveney , M. Nekovee , Proc. R. Soc. Lond. A 456 p 2043--2047(2000)
[18] S. M. Pickles , R. J. Blake , B. M. Boghosian , J. M. Brooke , J. Chin , P. E. L. Clarke , P. V. Coveney , R. Haines , J. Harting , M. Harvey , S. Jha , M. A. S. Jones , M. McKeown , R. K. Pinning , A. R. Porter , K. Roy , M. Riding , Proceedings of the Workshop on Case Studies on Grid Applications at GGF 10 (2004) http://www.zib.de/ggf/apps/meetings/ggf10.shtml
[19] J. Chin , J. Harting , S. Jha , P. V. Coveney , A. R. Porter , S. M. Pickles , Contemporary Physics 44 p 417--434(2003) doi:10.1080/00107510310001605046
 Close
Close

