UCL students win 2023 IBM Open Quantum Science Prize

Three UCL students in Chemistry, Physics and Astronomy and the London Centre for Nanotechnology placed first out of over 130 applications to share $30,000.

UCL students Tim Weaving (UCL Chemistry / EPSRC Centre for Doctoral Training in Delivering Quantum Technologies at the London Centre for Nanotechnology), Dr Alexis Ralli (UCL Chemistry), and Vinul Wimalaweera (UCL Physics and Astronomy) placed first in IBM’s international Quantum Open Science Prize. 

Founded in 2020, the prize brings the quantum community together to tackle useful problems in the field and present open-source solutions. This year’s theme was quantum state preparation – turning a known quantum state into another known quantum state. The submissions were judged based on performance, scalability, and most importantly, creativity. 

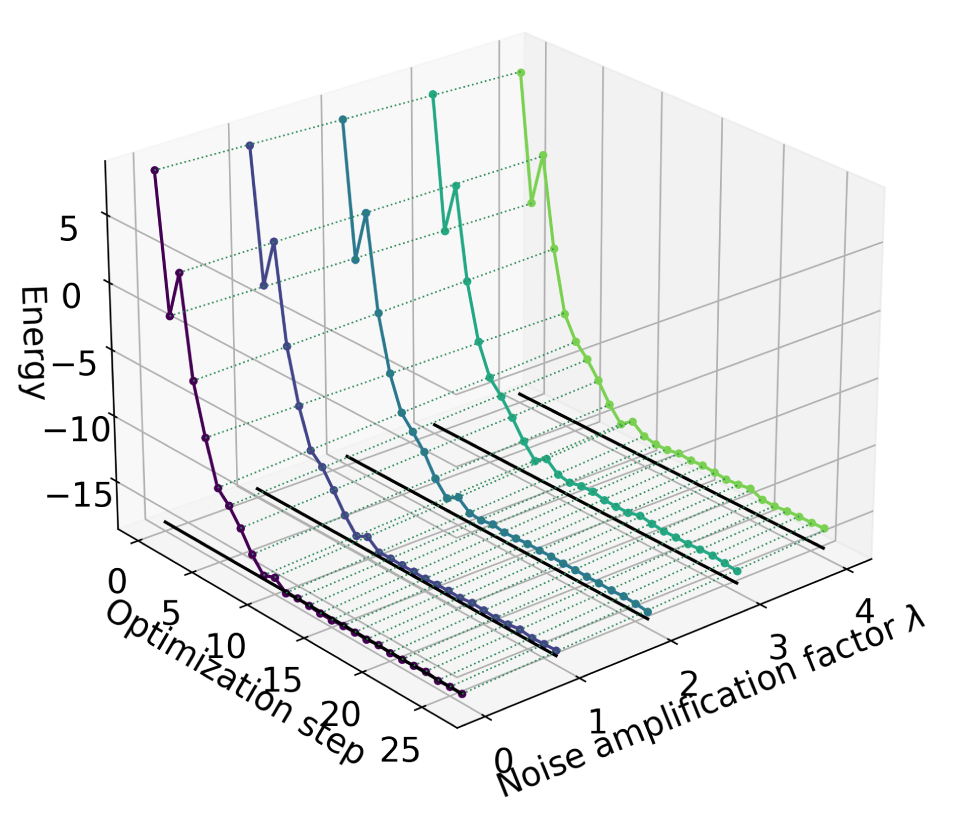
Participants were given a complex task to prepare a special kind of state in the world of quantum physics – the highly frustrated ground state of a Heisenberg spin-1/2 model on a Kagome lattice using the Variational Quantum Eigensolver (VQE) algorithm on Falcon, IBM’s most advanced quantum computing device available.

The organisers selected this problem because it is important for improving quantum computer efficiency. The state they were trying to create is like a unique fingerprint in the quantum world, and understanding it is at the forefront of quantum research.

UCL students managed to solve this complex problem with fewer resources and made the results much more reliable.

Student Tim Weaving, said: “A rule for the challenge was that only installable Python packages were allowed for the submission, however, our approach to solving the problem posed by IBM used code that was largely developed for our PhD research. 

“As such, in order for our submission to be valid we had to make a concerted effort to publish our software on the Python Package Index (PyPI), which required considerable work but ultimately was worth it, not just because it meant that we won the IBM challenge, but also as this contribution of our code to the public will hopefully provide utility for others in the field of quantum computing research.”

The UCL team’s submission effectively utilised advanced methods, specifically qubit tapering and contextual subspace VQE with density matrix renormalisation group (DMRG). Qubit tapering decreases the number of required qubits for quantum simulations by taking advantage of symmetries in the system being simulated. 

Contextual subspace VQE uses both classical and quantum VQE computations to approximate the ground state energy of a Hamiltonian more accurately and additionally reduces the number of qubits required. By using these techniques together, students were able to shrink the problem from needing 12 qubits down to just five.

Then, they ran their five-qubit experiments at the same time to get results faster. Combining these with quantum error mitigation methods like Zero-Noise Extrapolation and Readout Error Mitigation, they reduced errors in their quantum calculations and made the results much more accurate.

Commenting on the win, Tim Weaving added: “We are of course thrilled that the judges identified the novelty of our simulation methodology. When the results came back from being executed on the IBM quantum processor and we saw the error that had been achieved it was a real moment of justification for all the prior work we had put into developing our various quantum algorithms and it was very reassuring to see it all working in practice. 

“It has given us confidence that our research is headed in the right direction and has spurred us on to continue developing our ideas and contributing to the quantum technology community.”
 

Links

• Find out more about the IBM Open Quantum Science Prize
• Find out more about the EPSRC Centre for Doctorial training in Delivering Quantum Technologies
• UCL Chemistry  
• UCL Physics and Astronomy  

Image

• Top: (left to right) Tim Weaving, Dr Alexis Ralli and Vinul Wimalaweera.
• Bottom: The resulting error-mitigated VQE optimisation routine. The energy comes very close to the true ground state energy of -18, with a final error ratio of just 0.08% (well below the 1% threshold required for consideration in the competition).

---