ICML 2020

Taking place virtually between 12th July – 18th July 2020, ICML is widely regarded as one of the most respected international conferences in the AI Community. With nine accepted papers, UCL is the best represented contributor to the conference from Universities in the UK. In addition to papers, invited talks and workshops (detailed below), the Centre’s Deputy Director, Professor Marc Deisenroth, is a member of the ICML Organising Committee, undertaking the role of one of the conference’s Expo Chairs.

Speaking ahead of ICML 2020, Marc said, “It is a great privilege to be a member of the ICML 2020 Organising Committee, and as Deputy Director of UCL’s AI Centre, it is wonderful to see the work of academics within our own research centre so well represented at the conference. I’m very much looking forward to the event and engaging with the latest work from our wider AI research community.”

Accepted papers at ICML 2020 with authors from the AI Centre 

Self-Attentive Hawkes Process

Authors: Qiang Zhang (University College London) · Aldo Lipani (University College London) · Omer Kirnap (University College London) · Emine Yilmaz (University College London)

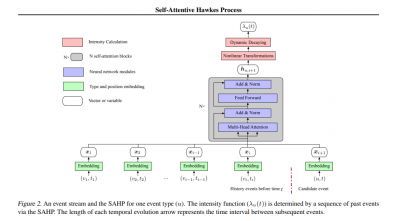
Paper Synopsis: We investigate the usefulness of self-attention to temporal point processes by proposing a Self-Attentive Hawkes Process (SAHP). The SAHP employed self-attention to summarize influence from history events and compute the probability of the next event. One deficit of the conventional self-attention is that position embeddings only considered order numbers in a sequence, which ignored time intervals between temporal events. To overcome this deficit, we modified the conventional method by translating time intervals into phase shifts of sinusoidal functions. Experiments on goodness-of-fit and prediction tasks showed the improved capability of SAHP. Furthermore, the SAHP is more interpretable than RNN-based counterparts because the learnt attention weights revealed contributions of one event type to the happening of another type. To the best of our knowledge, this is the first work that studies the effectiveness of self-attention in Hawkes processes

Spread Divergences

Authors: Mingtian Zhang (University College London) · Peter Hayes (University College London) · Thomas Bird (University College London) · Raza Habib (University College London) · David Barber (University College London)

Paper Synopsis: For distributions p and q with different supports, the divergence D(p||q) may not exist. We define a spread divergence SD(p||q) on modified p and q and describe sufficient conditions for the existence of such a divergence. We demonstrate how to maximize the discriminatory power of a given divergence by parameterizing and learning the spread. We also give examples of using a spread divergence to train and improve implicit generative models, including linear models (Independent Components Analysis) and non-linear models (Deep Generative Networks). 

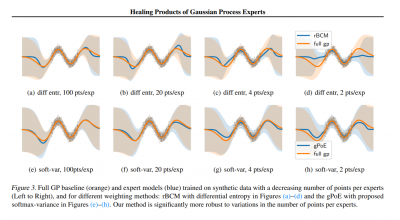
Healing Products of Gaussian Process Experts

Authors: Samuel Cohen (University College London) · Rendani Mbuvha (University of the Witwatersrand) · Tshilidzi Marwala (University of Johannesburg) · Marc Peter Deisenroth (University College London)

Paper Synopsis: Gaussian processes are nonparametric Bayesian models that have been applied to regression and classification problems. One of the approaches to alleviate their cubic training cost is the use of local GP experts trained on subsets of the data. In particular, product-of-expert models combine the predictive distributions of local experts through a tractable product operation. While these expert models allow for massively distributed computation, their predictions can suffer from erratic behaviour of the mean or uncalibrated uncertainty quantification. By calibrating predictions via tempered softmax weighting, we provide a solution to these problems for multiple product-of-expert models, including the generalised product of experts and the robust Bayesian committee machine. Furthermore, we leverage the optimal transport literature and propose a new product-of-expert model that combines predictions of local experts by computing their Wasserstein barycenter, which can be applied to both regression and classification.

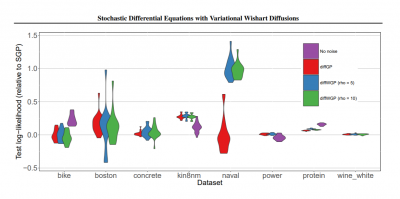
Stochastic Differential Equations with Variational Wishart Diffusions

Authors: Martin Jørgensen (Technical University of Denmark) · Marc Peter Deisenroth (University College London) · Hugh Salimbeni (G-Research)

Paper Synopsis: We present a Bayesian non-parametric way of inferring stochastic differential equations for both regression tasks and continuous-time dynamical modelling. The work has high emphasis on the stochastic part of the differential equation, also known as the diffusion, and modelling it with Wishart processes. Further, we present a semi-parametric approach that allows the framework to scale to high dimensions. This successfully led us on to how to model both latent and autoregressive temporal systems with conditional heteroskedastic noise. Experimentally, we verify that modelling diffusion often improves performance and that this randomness in the differential equation can be essential to avoid overfitting.

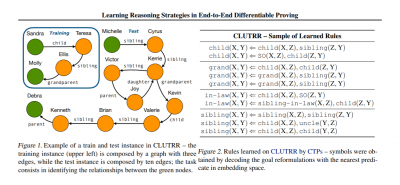
Learning Reasoning Strategies in End-to-End Differentiable Proving

Authors: Pasquale Minervini (University College London) · Sebastian Riedel (University College London, Facebook AI Research) · Pontus Stenetorp (University College London) · Edward Grefenstette (University College London, Facebook AI Research) · Tim Rocktäschel (University College London, Facebook AI Research) 

Paper Synopsis: Neural Theorem Provers (NTPs) are a continuous relaxation of the Backward Chaining logic reasoning algorithm, where comparisons between symbols are replaced by a differentiable similarity function between their embedding representations: they can induce interpretable rules and learn representations from data via back-propagation while providing logical explanations for their predictions. Their main limitation is that they are constrained by their computational complexity, as they need to consider all possible proof paths for proving a goal, deeming them infeasible for many real-world applications. In this paper, we introduce Conditional Theorem Provers (CTPs), a family of NTP variants that learns an optimal rule selection strategy via gradient-based optimisation: CTPs can dynamically generate rules on-the-fly conditioned on the goal, rather than iterating over a possibly very large knowledge base. We show that CTPs are significantly more accurate and efficient than their predecessors, and yield state-of-the-art results on the CLUTRR dataset, which tests the systematic generalisation properties of neural models. Finally, CTPs show better link prediction results on standard benchmarks in comparison with other neuro-symbolic reasoning models, while retaining their explainability properties

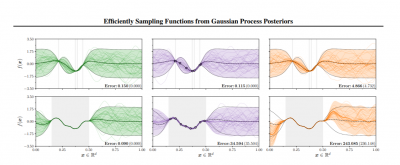
Efficiently Sampling Functions from Gaussian Process Posteriors

Authors: James Wilson (Imperial College London) · Viacheslav Borovitskiy (Saint Petersburg State University) · Alexander Terenin (Imperial College London) · Peter Mostowsky (Saint Petersburg State University) · Marc Peter Deisenroth (University College London)

Paper Synopsis: Gaussian processes are the gold standard for many real-world modelling problems, especially in cases where a model's success hinges upon its ability to faithfully represent predictive uncertainty. These problems typically exist as parts of larger frameworks, where quantities of interest are ultimately defined by integrating over posterior distributions. However, these algorithms' inner workings rarely allow for closed-form integration, giving rise to a need for Monte Carlo methods. Despite substantial progress in scaling up Gaussian processes to large training sets, methods for accurately generating draws from their posterior distributions still scale cubically in the number of test locations. We identify a decomposition of Gaussian processes that naturally lends itself to scalable sampling by enabling us to efficiently generate functions that accurately represent their posteriors. Building off of this factorization, we propose decoupled sampling, an easy-to-use and general-purpose approach for fast posterior sampling. Decoupled sampling works as a drop-in strategy that seamlessly pairs with sparse approximations to Gaussian processes to afford scalability both during training and at test time. In a series of experiments designed to test competing sampling schemes' statistical behaviors and practical ramifications, we empirically show that functions drawn using decoupled sampling faithfully represent Gaussian process posteriors at a fraction of the usual cost.

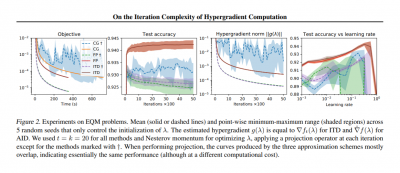
On the Iteration Complexity of Hypergradient Computations

Authors: Riccardo Grazzi (Istituto Italiano di Tecnologia and University College London) · Luca Franceschi (Istituto Italiano di Tecnologia and University College London) · Massimiliano Pontil (Istituto Italiano di Tecnologia and University College London) · Saverio Salzo (Istituto Italiano di Tecnologia)

Paper Synopsis: We study a general class of bilevel problems, consisting in the minimization of an upper-level objective which depends on the solution to a parametric fixed-point equation. Important instances arising in machine learning include hyperparameter optimization, meta-learning, and certain graph and recurrent neural networks. Typically the gradient of the upper-level objective (hypergradient) is hard or even impossible to compute exactly, which has raised the interest in approximation methods. We investigate some popular approaches to compute the hypergradient, based on reverse mode iterative differentiation and approximate implicit differentiation. Under the hypothesis that the fixed point equation is defined by a contraction mapping, we present a unified analysis which allows for the first time to quantitatively compare these methods, providing explicit bounds for their iteration complexity. This analysis suggests a hierarchy in terms of computational efficiency among the above methods, with approximate implicit differentiation based on conjugate gradient performing best. We present an extensive experimental comparison among the methods which confirm the theoretical findings.

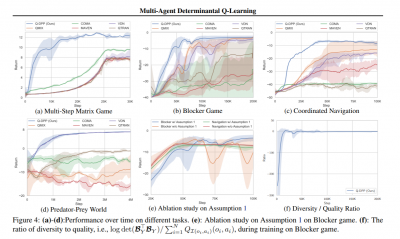
Multi-Agent Determinantal Q-Learning

Authors: Yaodong Yang (Noah's Ark Lab, Huawei / University College London) · Ying Wen (University College London) · Liheng Chen (Shanghai Jiao Tong University) · Jun Wang (University College London) · Kun Shao (Noah's Ark Lab, Huawei) · David Mguni (Noah's Ark Lab, Huawei) · Weinan Zhang (Shanghai Jiao Tong University)

Paper Synopsis: Centralized training with decentralized execution has become an important paradigm in multi-agent learning. Though practical, current methods rely on restrictive assumptions to decompose the centralized value function across agents for execution. In this paper, we eliminate this restriction by proposing multi-agent determinantal Q-learning. Our method is established on Q-DPP, an extension of determinantal point process (DPP) with partition-matroid constraint to multi-agent setting. Q-DPP promotes agents to acquire diverse behavioral models; this allows a natural factorization of the joint Q-functions with no need for a priori structural constraints on the value function or special network architectures. We demonstrate that Q-DPP generalizes major solutions including VDN, QMIX, and QTRAN on decentralizable cooperative tasks. To efficiently draw samples from Q-DPP, we adopt an existing sample-by-projection sampler with theoretical approximation guarantee. The sampler also benefits exploration by coordinating agents to cover orthogonal directions in the state space during multi-agent training. We evaluate our algorithm on various cooperative benchmarks; its effectiveness has been demonstrated when compared with the state-of-the-art.

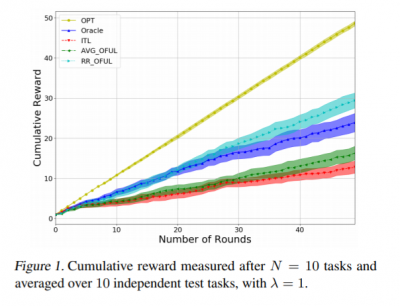
Meta-learning with Stochastic Linear Bandits

Authors: Leonardo Cella (University of Milan) · Alessandro Lazaric (Facebook AI Research) · Massimiliano Pontil (Istituto Italiano di Tecnologia and University College London)

Paper Synopsis: We investigate meta-learning procedures in the setting of stochastic linear bandits tasks. The goal is to select a learning algorithm which works well on average over a class of bandits tasks, that are sampled from a task-distribution. Inspired by recent work on learning-to-learn linear regression, we consider a class of bandit algorithms that implement a regularized version of the well known OFUL algorithm, where the regularization is a square euclidean distance to a bias vector. We first study the benefit of the biased OFUL algorithm in terms of regret minimization. We then propose two strategies to estimate the bias within the learning-to-learn setting. We show both theoretically and experimentally, that when the number of tasks grows and the variance of the task-distribution is small, our strategies have a significant advantage over learning the tasks in isolation.

Invited Talks 

Tim Rocktäschel will give an invited talk about "The NetHack Learning Environment" at the ICML Workshop on Learning in Artificial Open Worlds: https://sites.google.com/view/icml-laow2020/

Workshops 

Edward Grefenstette and Tim Rocktäschel are co-organising the First Workshop on Language for Reinforcement Learning (LaReL) at ICML 2020. Information about the workshop can be found here: https://larel-ws.github.io/