
Associate Professor, Department of Mathematics, University College London, Gower Street, London WC1E 6BT
Office: 802B, Phone: 020 679 3593 (33593 internal)
E-mail: s.baigent_at_ucl.ac.dot.uk
Current Research Interests
- Invariant manifolds for Kolmogorov equations
- Curvature of Invariant Manifolds
- Difference Equations
- Quasilinkage Equilibrium in Genetics
- Global stability for ecological systems
- Monotone dynamical systems
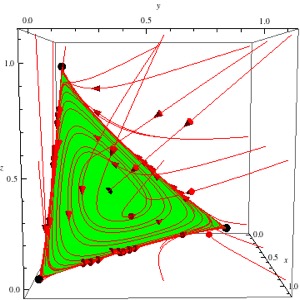
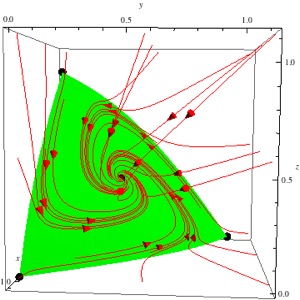
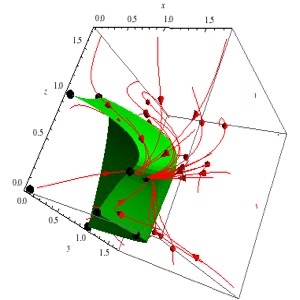
Figures: Invariant manifolds for Lotka-Volterra systems. Last figure is a non-competitive example. Local stability is related to curvature of the manifold at a fixed point.
Teaching
• MATH3506 Mathematical Ecology
• MATHM505 Evolutionary Games and Population Genetics
Recent Publications
Baigent, S, Ching, A. (Under review) Balance simplices of 3-species May-Leonard systems. (pdf)
Baigent, S., Seymenoglu, B. (2020) Invariant manifolds of Competitive Selection-Recombination dynamics. Nonlinear Analysis Series B: Real World Applications, Vol 53 (June, available online) (pdf)
Ching, A., Baigent, S. (2019) Manifolds of Balance in Planar Ecological Systems, Journal for Mathematics and Computation 358, 204-215. (pdf)
Ching, A., Baigent, S. (2019) The balance simplex in non-competitive 2-species scaled Lotka-Volterra systems Journal of Biological Dynamics. 13:1, 128-147 (pdf)
Baigent, S. (2019) Convex geometry of the carrying simplex for the May-Leonard map. Discrete & Continuous Dynamical Systems - Series B, 24(4), 1697–1723 (pdf)
.
Baigent, S. (2019) Carrying simplices for competitive systems. Proceedings of ICDEA 2017. (pdf)
Seymenoglu, B. & Baigent, S. (2018) Nonmonotone invariant manifolds in the Nagylaki–Crow model. Nonlinear Analysis Series B: Real World Applications, 41, 570–587. (pdf)
Baigent, S., & Hou, Z. (2017). Global stability of discrete-time competitive population models. Journal of Difference Equations and Applications, 8, 1–19. (pdf)
Baigent, S. (2016) Convexity of the carrying simplex for discrete-time planar competitive Kolmogorov systems. Journal of Difference Equations and Applications, 22(5), 609-622. (pdf)
Baigent, S. (2016) Lotka-Volterra Dynamics: An Introduction. DYNAMICAL AND COMPLEX SYSTEMS, LTCC Advanced Mathematics Series, World Scientific. (pdf)
Hou, Z. & Baigent. (2015) Global stability and repulsion in autonomous Kolmogorov systems. Communications of Pure and Applied Analysis, 14(3), 1205-1238. (pdf)
Hou, Z. and Baigent, S. (2013) Heteroclinic limit cycles in competitive Kolmogorov systems. Discrete and Continuous Dynamical Systems - Series A, 33(9), 4071-4093. (pdf)
Baigent, S. (2013) Geometry of carrying simplices of 3-species competitive Lotka-Volterra systems. Nonlinearity 26(4), 1001-1029 (pdf)
Nattrass, S., Baigent, S., Murrell D. (2012) Quantifying the likelihood of coexistence for communities with asymmetric competition, Bulletin of Mathematical Biology. Vol 74, No. 10, 2315-2338. (pdf)
Baigent, S and Hou, Z. (2012) On the global stability of fixed points for Lotka-Volterra systems. Differential Equations and Dynamical Systems. 20(1), 53-66. (pdf)
Baigent, S. (2012) Convexity-preserving flows of totally competitive planar Lotka-Volterra equations and the geometry of the carrying simplex. Proceedings of the Edinburgh Mathematical Society Vol 55. No 1, 53-63. (pdf)
Hou, Z. and Baigent, S. (2011) Fixed Point Global Attractors and Repellors in Competitive Lotka-Volterra Systems. Dynamical Systems Vol 26, No. 4. 367-390. (pdf)
Model building at its best?