Quantum advantage from long-range interactions

Researchers at UCL, University of Florence, and Istituto Nazionale di Fisica Nucleare (INFN) have shown the possibility of a quantum speedup in noisy quantum devices with permanent long-range interactions. In systems with long-range interactions, the researchers have found the interaction ranges that can solve the spatial search problem optimally fast – quadratically faster than it is possible on a classical computer.

The spatial search problem is central to many algorithms and real-life applications. It involves finding a special site in space which is distinct from all the others. For example, finding a pixel of a particular colour in an image.

In classical computing algorithms, using random samplers, the special site can only be found by successively looking at all the sites one at a time. In systems with a large number of sites this process can take a very long time.

Quantum computing provides a shortcut. By using a type of quantum algorithm called a ‘quantum walker’ – which is allowed in move in superposition to multiple sites at once – the special site can be found much quicker. This quantum ‘speedup’ is called quadratic advantage because the quantum walker can find the special site in the square root of the time it would take a classical algorithm. This is the optimal time it would take a quantum algorithm to find the site.

While optimal quadratic advantage exists in systems were there are many possible interactions between sites, it has been shown to be impossible for systems arranged in a one-dimensional chain where the sites can only interact with their nearest-neighbour. This is because the quantum walker can only hop from site to site in one step along the chain, which is exactly how a classical walker would progress.

UCL-led research published in Physical Review Letters by Dylan Lewis (UCL), Asmae Benhemou (UCL), Natasha Feinstein (UCL), Leonardo Banchi (University of Florence & INFN) and Professor Sougato Bose (UCL) demonstrates that quadratic quantum advantage can exist in one-dimensional systems if the quantum walker can make use of long-range interactions between sites.

Corresponding author and UCL EPSRC Centre for Doctoral Training in Delivering Quantum Technologies student Dylan Lewis said: “By considering long-range interactions, we essentially allow a quantum walker to hop long distances in one step which allows the optimal quadratic advantage to be reinstated. Also, by tuning the range of these interactions, we found and proved the existence of a transition between a regime where the quantum speedup exists and a regime where it does not.”

Co-author Professor Sougato Bose (UCLQ and UCL Physics & Astronomy) said: “While discovering that this type of optimal spatial search exists in theory is exciting, we are thrilled to find that this type of quantum advantage should be experimentally realisable using quantum computing hardware devices today.”

In the study, the team show that the type of optimal quadratic advantage they describe should be experimentally realisable in a single one-dimensional register in a current ion-trap setup. The researchers think that this could provide the basis for a useful demonstration of quantum advantage in the noisy intermediate-scale quantum devices which are currently available.

A quantum computer harnesses laws of physics that are normally seen only at the atomic and subatomic level (for instance, that particles can be in two places simultaneously). Quantum computers could be more powerful than today’s super computers and capable of performing complex calculations that are otherwise practically impossible.

However, currently available quantum computers have relatively few quantum bits and are subject to interference. These noisy intermediate scale quantum computers are prone to errors and do not yet have the computational resources needed to directly simulate large quantum systems.

While the applications of quantum computing differ from traditional computers, they will enable us to solve certain types of problems that cannot be solved on classical computers. These include problems that involve quantum mechanics directly such as drug development, but will also help optimise the solutions to complex everyday problems such as transport and logistics.

This research received funding from the UK Engineering and Physical Sciences Research Council and the programme ‘Rita Levi Montalcini’ for young researchers.

Links:

• Read the full paper in Physical Review Letters
• Find out more about UCL’s EPSRC Centre for Doctorial Training in Delivering Quantum Technologies

Image:

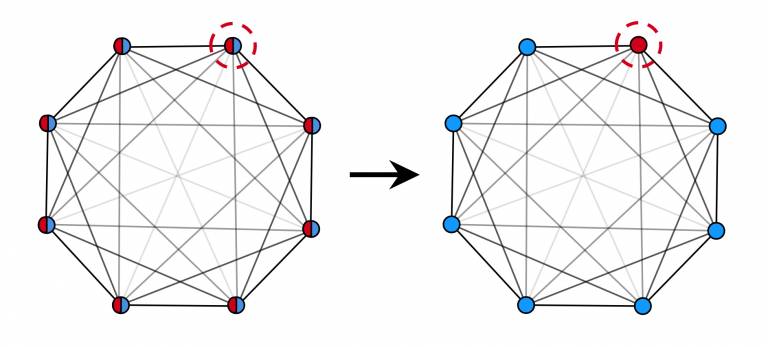
Illustration of optimal spatial search using long-range interactions. The opacity of the edges (grey-black) indication the relative interaction strengths, where more transparent edges mean weaker interaction. Red and blue dots represent the two possible states at each site, with half and half for a quantum superposition of both states. The dashed red circle shows the special marked site. (Credit: D. Lewis, UCL)