
Gower Street
London WC1E 6BT, UK
Tel: +44-(0)20-7679-2727
Fax: +44-(0)20-7380-0986
E-mail: g.heijden@ucl.ac.uk
|
|
Gower Street |
"Many a golden opportunity to remain silent has been squandered by anti-prophets who do not realise that the grounds for declaring something impossible or inconceivable may be undermined by new ideas that cannot be foreseen."
Peter Medawar (1965)







 Electrodynamic tethers connect spacecraft to other orbiting bodies and are
designed to use the earth's magnetic field, rather than chemical fuel, for
thrust and drag. Some tethers are spun about their axis for gyroscopic
stability and therefore must resist bending and twisting. Such tethers need
to be described by an elastic rod rather than the traditional string. Of
particular interest are whirling and other instabilities.
J. Phys. A paper (2008) (on the integrability of a rod in a
magnetic field)
[arXiv preprint]
J. Phys. A paper (2009) (on spatial chaos of an EXTENSIBLE rod
in a magnetic field)
[arXiv preprint]
J. Nonl. Sci. paper (2010) (on magnetically-induced buckling of
electrodynamic space tethers)
[arXiv preprint]
J. Phys. A paper (2011) (on a Melnikov method and nonintegrability
of an extensible rod in a magnetic field)
[arXiv preprint]
Physica D paper (2014) (on localised electrodynamic space tether
solutions and their bifurcations)
As a spin-off, in this ZAMP paper (2014)
we give the first correct proof that the nonsymmetric top, and hence the
anisotropic rod, is chaotic.
Electrodynamic tethers connect spacecraft to other orbiting bodies and are
designed to use the earth's magnetic field, rather than chemical fuel, for
thrust and drag. Some tethers are spun about their axis for gyroscopic
stability and therefore must resist bending and twisting. Such tethers need
to be described by an elastic rod rather than the traditional string. Of
particular interest are whirling and other instabilities.
J. Phys. A paper (2008) (on the integrability of a rod in a
magnetic field)
[arXiv preprint]
J. Phys. A paper (2009) (on spatial chaos of an EXTENSIBLE rod
in a magnetic field)
[arXiv preprint]
J. Nonl. Sci. paper (2010) (on magnetically-induced buckling of
electrodynamic space tethers)
[arXiv preprint]
J. Phys. A paper (2011) (on a Melnikov method and nonintegrability
of an extensible rod in a magnetic field)
[arXiv preprint]
Physica D paper (2014) (on localised electrodynamic space tether
solutions and their bifurcations)
As a spin-off, in this ZAMP paper (2014)
we give the first correct proof that the nonsymmetric top, and hence the
anisotropic rod, is chaotic.
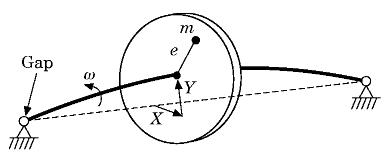 Bearing clearance introduces a nonlinearity into rotor dynamics, which
gives rise to complicated dynamics. We study resonances and mode-locking
of (quasi-)periodic solutions and have foound an interesting new
interaction between mode-locking and homoclinic phenomena (coined the
zipper bifurcation).
[
J. Nonlinear Sci. (1995)] (on resonance and mode-locking)
[
Dynamics and Stability of Systems (2000)] (on interaction between
mode-locking and homoclinic behaviour - the zipper)
[
Chaos, Solitons & Fractals (1993)] (application to drill string
dynamics - resonant and chaotic drill string whirl)
Bearing clearance introduces a nonlinearity into rotor dynamics, which
gives rise to complicated dynamics. We study resonances and mode-locking
of (quasi-)periodic solutions and have foound an interesting new
interaction between mode-locking and homoclinic phenomena (coined the
zipper bifurcation).
[
J. Nonlinear Sci. (1995)] (on resonance and mode-locking)
[
Dynamics and Stability of Systems (2000)] (on interaction between
mode-locking and homoclinic behaviour - the zipper)
[
Chaos, Solitons & Fractals (1993)] (application to drill string
dynamics - resonant and chaotic drill string whirl)
 We study snarling and other twist-induced instabilities of transported
textile yarns in such industrial processes as ring-spinning and texturing.
We are also trying to get a better understanding of the mechanical
properties of textile yarns (such as the twist-stretch coupling) in terms
of the properties of the composing fibres.
[
J. Eng. Math. (2007)] (paper on the snarling instability)
[
J. Text. Inst. (2008)] (paper on multi-ply textile yarns)
[
J. Text. Inst. (2010)] (paper on torsional properties of plied yarns)
We study snarling and other twist-induced instabilities of transported
textile yarns in such industrial processes as ring-spinning and texturing.
We are also trying to get a better understanding of the mechanical
properties of textile yarns (such as the twist-stretch coupling) in terms
of the properties of the composing fibres.
[
J. Eng. Math. (2007)] (paper on the snarling instability)
[
J. Text. Inst. (2008)] (paper on multi-ply textile yarns)
[
J. Text. Inst. (2010)] (paper on torsional properties of plied yarns)
 The structural support protein collagen is the most abundant protein in
the animal kingdom and helps tissues such as bone and tendon to withstand
stretching. Models of multi-strand plied structures are applied to the
rope-like collagen fibrils recently discovered in UCL's Medicine Department.
[
Biophysical Journal 92, 70-75 (2007)] (nanoscale ropes)
The structural support protein collagen is the most abundant protein in
the animal kingdom and helps tissues such as bone and tendon to withstand
stretching. Models of multi-strand plied structures are applied to the
rope-like collagen fibrils recently discovered in UCL's Medicine Department.
[
Biophysical Journal 92, 70-75 (2007)] (nanoscale ropes)
 Configurations and bifurcations of rods on or inside surfaces are studied
(i.e., equality or inequality constraints). An example of the latter is a
drill string bouncing inside a borehole. This work is also relevant for
structural problems in molecular biology (for instance, in the
supercoiling and packing of DNA).
[
Proc. R. Soc. Lond. A 457, 695-715 (2001)] (derives and
analyses the equations for an isotropic rod deforming on a cylinder -
heteroclinic connection)]
[
Int. J. Solids Struct. 39, 1863-1883 (2002)] (anisotropic
rod on a cylinder - spatial chaos (heteroclinic tangle), Maxwell critical
load for transition to periodic buckling)
[
Arch. Rat. Mech. Anal. 182, 471-511 (2006)] (on
energy-minimising self-contacting rods on a cylinder)
[arXiv preprint]
[
Quart. Appl. Math. 65, 385-402 (2007)] (on end rotation, twist and writhe for large-deformation rods)
[early arXiv preprint]
By modelling a rod on a cylinder as a special case of a two-strand braid
(see theory below), we now also have a complete theory of static friction,
allowing us to determine the dependence of critical loads of constrained
cylindrical buckling on friction parameters:
[
J. Mech. Phys. Solids 173, 105224 (2023) ]
The braid modelling also allows us to study the buckling and lift-off of
a heavy rod compressed into a cylinder with arbitrary inclination relative
to the direction of gravity. Gravity becomes an internal torque to the
braid. Buckling in near-horizontal cylinders is found to be dominated by
mode-switching, while buckling in near-vertical cylinders is dominated by
self-weight buckling at tensile loads. We show how the inclination angle
interpolates between these two scenarios.
[
J. Mech. Phys. Solids , 105464 (2023) ]
Configurations and bifurcations of rods on or inside surfaces are studied
(i.e., equality or inequality constraints). An example of the latter is a
drill string bouncing inside a borehole. This work is also relevant for
structural problems in molecular biology (for instance, in the
supercoiling and packing of DNA).
[
Proc. R. Soc. Lond. A 457, 695-715 (2001)] (derives and
analyses the equations for an isotropic rod deforming on a cylinder -
heteroclinic connection)]
[
Int. J. Solids Struct. 39, 1863-1883 (2002)] (anisotropic
rod on a cylinder - spatial chaos (heteroclinic tangle), Maxwell critical
load for transition to periodic buckling)
[
Arch. Rat. Mech. Anal. 182, 471-511 (2006)] (on
energy-minimising self-contacting rods on a cylinder)
[arXiv preprint]
[
Quart. Appl. Math. 65, 385-402 (2007)] (on end rotation, twist and writhe for large-deformation rods)
[early arXiv preprint]
By modelling a rod on a cylinder as a special case of a two-strand braid
(see theory below), we now also have a complete theory of static friction,
allowing us to determine the dependence of critical loads of constrained
cylindrical buckling on friction parameters:
[
J. Mech. Phys. Solids 173, 105224 (2023) ]
The braid modelling also allows us to study the buckling and lift-off of
a heavy rod compressed into a cylinder with arbitrary inclination relative
to the direction of gravity. Gravity becomes an internal torque to the
braid. Buckling in near-horizontal cylinders is found to be dominated by
mode-switching, while buckling in near-vertical cylinders is dominated by
self-weight buckling at tensile loads. We show how the inclination angle
interpolates between these two scenarios.
[
J. Mech. Phys. Solids , 105464 (2023) ]


 [
Journal of the Mechanics and Physics of Solids 64, 83-132 (2014)]
(equilibrium equations for elastic braids)
[
Soft Matter 9, 9833-9848 (2013)]
(application to dual-DNA braiding experiments)
[
Journal of the Mechanics and Physics of Solids 64, 83-132 (2014)]
(equilibrium equations for elastic braids)
[
Soft Matter 9, 9833-9848 (2013)]
(application to dual-DNA braiding experiments)
 Subsea pipelines under high-temperature conditions tend to relieve their
axial compressive stress by forming localised lateral or upheaval buckles.
This type of buckling has traditionally been studied as a kind of imperfect
column buckling problem. The first paper below studies lateral buckling as
a genuine localised buckling phenomenon governed by a different static
instability (a Hamiltonian-Hopf bifurcation) with a different critical load
and with post-buckling shapes described by homoclinic orbits. These
homoclinic orbits give analytical buckle decay rates without the need for
ad hoc assumptions on pipeline imperfections.
We also investigate by means of parameter studies how buckling can be
controlled by sleepers or buoyancy sections. We furthermore carry out
stability analyses that reveal a limit to the temperature difference for
safe operation of the pipeline.
[
Thin-Walled Structures 120, 408-420 (2017)]
(localised lateral buckling of partially embedded subsea pipelines with
nonlinear soil resistance)
[
Thin-Walled Structures 122, 17-29 (2018)]
(lateral buckling of pipelines with sleepers as buckle initiators)
[
Marine Structures 58, 199-222 (2018)]
(on distributed buoyancy sections to control lateral buckling)
[
Marine Structures 60, 165-185 (2018)]
(localised upheaval buckling of buried subsea pipelines)
[
Engineering Structures 168, 447-461 (2018)]
(on a different lateral buckling mode of pipelines with sleeper)
The paper below studies the shock sensitivity of a trenched pipeline (for
instance under irregular fluid flow inside the pipe, landslides or
earthquakes), i.e., the nonlinear stability under finite
disturbances rather than the usual linear stability under
infinitesimal perturbations.
[
Journal of the Mechanics and Physics of Solids 143, 104044
(2020)]
Subsea pipelines under high-temperature conditions tend to relieve their
axial compressive stress by forming localised lateral or upheaval buckles.
This type of buckling has traditionally been studied as a kind of imperfect
column buckling problem. The first paper below studies lateral buckling as
a genuine localised buckling phenomenon governed by a different static
instability (a Hamiltonian-Hopf bifurcation) with a different critical load
and with post-buckling shapes described by homoclinic orbits. These
homoclinic orbits give analytical buckle decay rates without the need for
ad hoc assumptions on pipeline imperfections.
We also investigate by means of parameter studies how buckling can be
controlled by sleepers or buoyancy sections. We furthermore carry out
stability analyses that reveal a limit to the temperature difference for
safe operation of the pipeline.
[
Thin-Walled Structures 120, 408-420 (2017)]
(localised lateral buckling of partially embedded subsea pipelines with
nonlinear soil resistance)
[
Thin-Walled Structures 122, 17-29 (2018)]
(lateral buckling of pipelines with sleepers as buckle initiators)
[
Marine Structures 58, 199-222 (2018)]
(on distributed buoyancy sections to control lateral buckling)
[
Marine Structures 60, 165-185 (2018)]
(localised upheaval buckling of buried subsea pipelines)
[
Engineering Structures 168, 447-461 (2018)]
(on a different lateral buckling mode of pipelines with sleeper)
The paper below studies the shock sensitivity of a trenched pipeline (for
instance under irregular fluid flow inside the pipe, landslides or
earthquakes), i.e., the nonlinear stability under finite
disturbances rather than the usual linear stability under
infinitesimal perturbations.
[
Journal of the Mechanics and Physics of Solids 143, 104044
(2020)]
 We study the shape and mechanics of animal whiskers and analogous robotic
sensing devices.
[
Science Advances (2020) (open access) paper on their universal
shape]
[ Journal of Morphology
(2020) (open access) paper with more on whisker shape]
[ Journal of Morphology
(2023) (open access) paper on the variation of whisker shape between
species]
[
Soft Robotics (2023) on selecting appropriate base measurements in
whisker sensing]
We study the shape and mechanics of animal whiskers and analogous robotic
sensing devices.
[
Science Advances (2020) (open access) paper on their universal
shape]
[ Journal of Morphology
(2020) (open access) paper with more on whisker shape]
[ Journal of Morphology
(2023) (open access) paper on the variation of whisker shape between
species]
[
Soft Robotics (2023) on selecting appropriate base measurements in
whisker sensing]
 We study the mechanics of inextensible strips with applications to paper
crumpling, fabric draping as well as general sheet processing. Geometrically
this leads to the study of developable surfaces (surfaces flat in one
direction). As part of this work we solved the long-standing problem of
finding the shape of a Möbius strip.
We study the mechanics of inextensible strips with applications to paper
crumpling, fabric draping as well as general sheet processing. Geometrically
this leads to the study of developable surfaces (surfaces flat in one
direction). As part of this work we solved the long-standing problem of
finding the shape of a Möbius strip.



 Our paper `The shape of a Möbius strip' has now appeared in
Nature Materials (2007)
Our paper `The shape of a Möbius strip' has now appeared in
Nature Materials (2007)
(a preprint can be found here, Supplementary Information here; or read the abstract, or UCL's top story)
See Eugene's page for publicity
Extending this work, we have discovered and described a new triangular buckling pattern of twisted inextensible strips held in tension with edge stress concentration similar to that of the Möbius strip (Proc. R. Soc. A (2010) paper, arXiv preprint):


We have also computed equilibrium shapes of knotted one-sided ribbons such as these (2,5) and (3,7) torus knots:
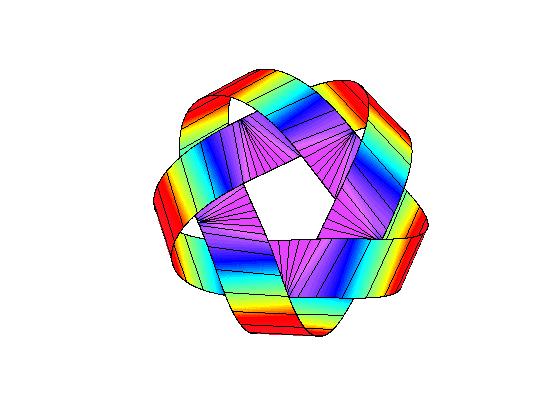
By contrast, the (2,3) (trefoil) and (4,7) knots look like:

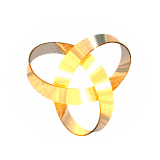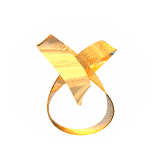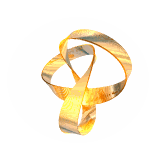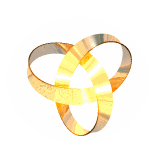
(note that one-sided closed inextensible ribbons need to have an odd number of inflection/switching points (with accompanying singularity in the bending energy density); the (2,3) trefoil knot has these on the outside and therefore looks somewhat different from the usual shape (right), requiring a wider berth to accommodate them; we call it a type II torus knot)
For more on such strips with topology different from the Möbius one, see our paper in the Journal of Elasticity (2015)
A singular perturbation analysis of these universal cone-like singularities on the edge of the strip has been published in the Journal of the Mechanics and Physics of Solids (2023)
The method for deriving convenient equilibrium equations for general one-dimensional elastic problems (i.e., for geometric variational problems on curves) is discussed in our paper in Physical Review E (2009) [arXiv preprint] Quantum eigenstates of a particle confined to the surface of a Möbius strip (or other one-sided surface) reveal curvature trapping in regions (creases) of high curvature as the strip's width-to-length ratio is increased. This could be important for transport properties of Möbius-type structures in nanoscale devices. See our paper in the Journal of Physics: Condensed Matter (2009) [arXiv preprint] We have also applied our methods to helical ribbons and discovered tension-induced multistability and phase separation (straightening) as observed in cholesterol ribbons. The results may also be relevant for nanobelts and the design of nanoswitches [Physical Review Letters 101, 084301 (2008)] [arXiv preprint]: How to shed a loop in a kinked helical spring:
How to shed a loop in a kinked helical spring:
 Helical nanoribbons of various types of material (SiO2, ZnO, Si/Cr, SiGe/Si,
SiGe/Si/Cr) have been fabricated for use in nano-electromechanical systems
(NEMS) such as nanoinductors, resonators, actuators, etc. Of particular
interest are nanosprings of very low pitch as they allow for a large magnetic
flux density. Such low-pitch springs when pulled may not simply unwind but
instead show a highly nonlinear force-extension response dominated by
sequential multi-loop pop-out.
[J. Mech. Phys. Solids 57, 959-969 (2009)]
[arXiv preprint]
Helical nanoribbons of various types of material (SiO2, ZnO, Si/Cr, SiGe/Si,
SiGe/Si/Cr) have been fabricated for use in nano-electromechanical systems
(NEMS) such as nanoinductors, resonators, actuators, etc. Of particular
interest are nanosprings of very low pitch as they allow for a large magnetic
flux density. Such low-pitch springs when pulled may not simply unwind but
instead show a highly nonlinear force-extension response dominated by
sequential multi-loop pop-out.
[J. Mech. Phys. Solids 57, 959-969 (2009)]
[arXiv preprint]
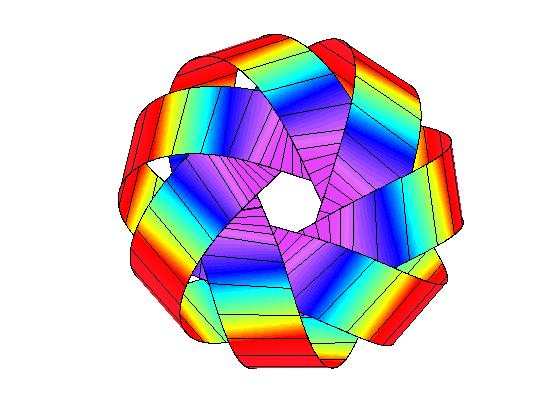
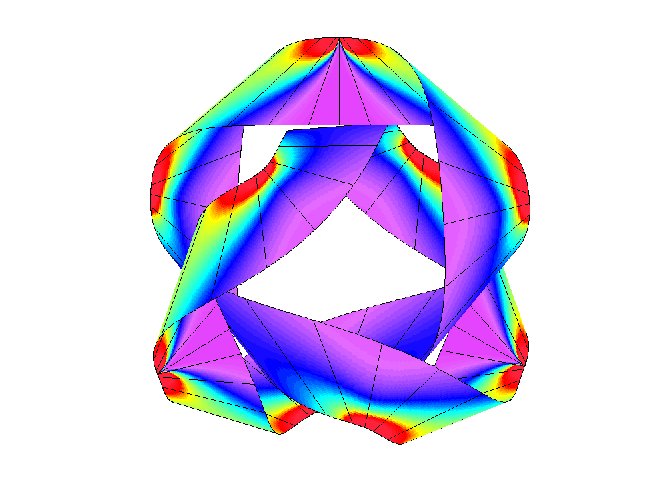
 Closed annular strips can be folded into compact shapes in 'regular' or
'inverted' fashion. Wide-strip equilibrium configurations can be either
inflectional or non-inflectional. Inflectional solutions have stress
localisations, with diverging strain energy density, on the edge of the strip.
Closed annular strips can be folded into compact shapes in 'regular' or
'inverted' fashion. Wide-strip equilibrium configurations can be either
inflectional or non-inflectional. Inflectional solutions have stress
localisations, with diverging strain energy density, on the edge of the strip.
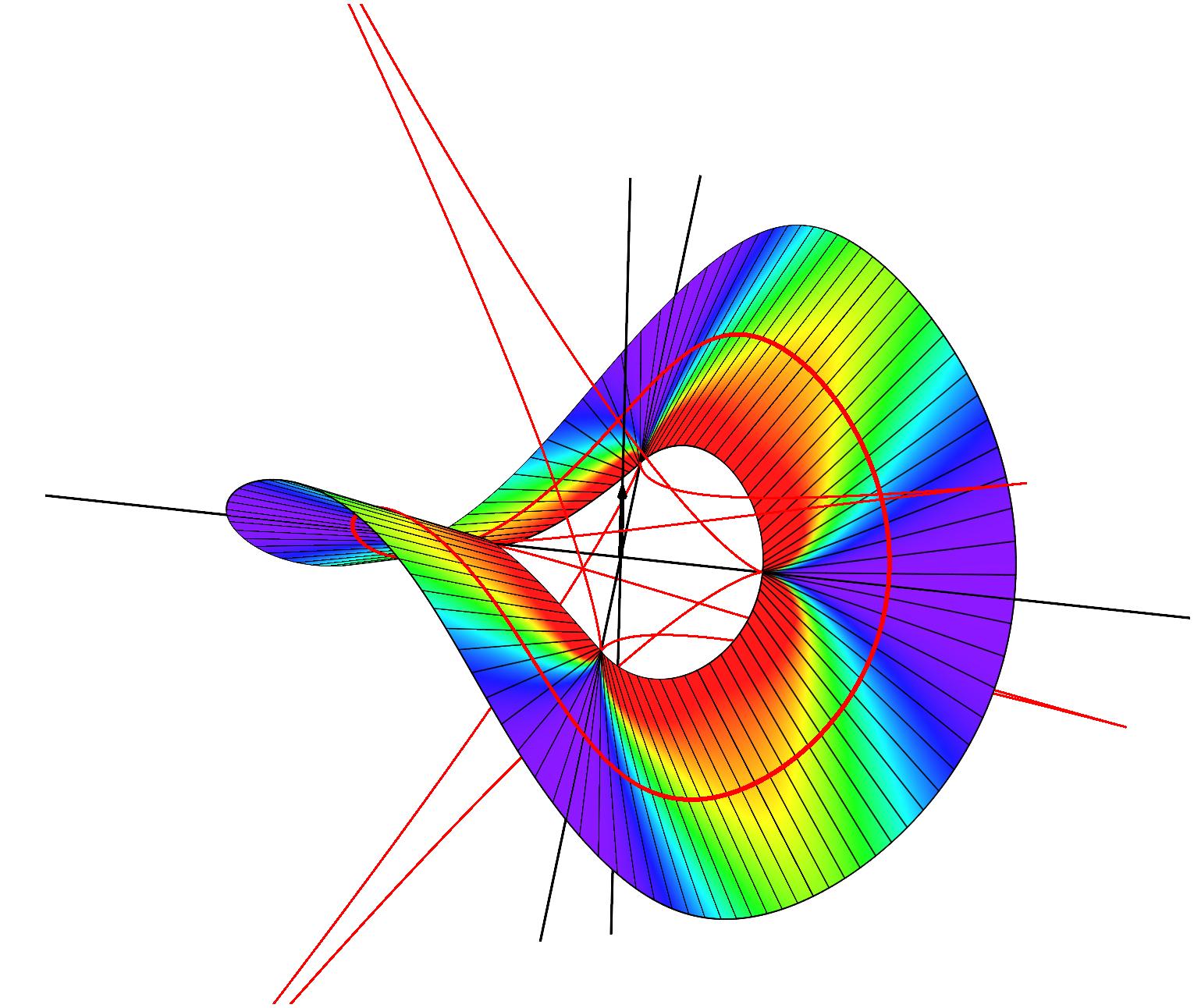
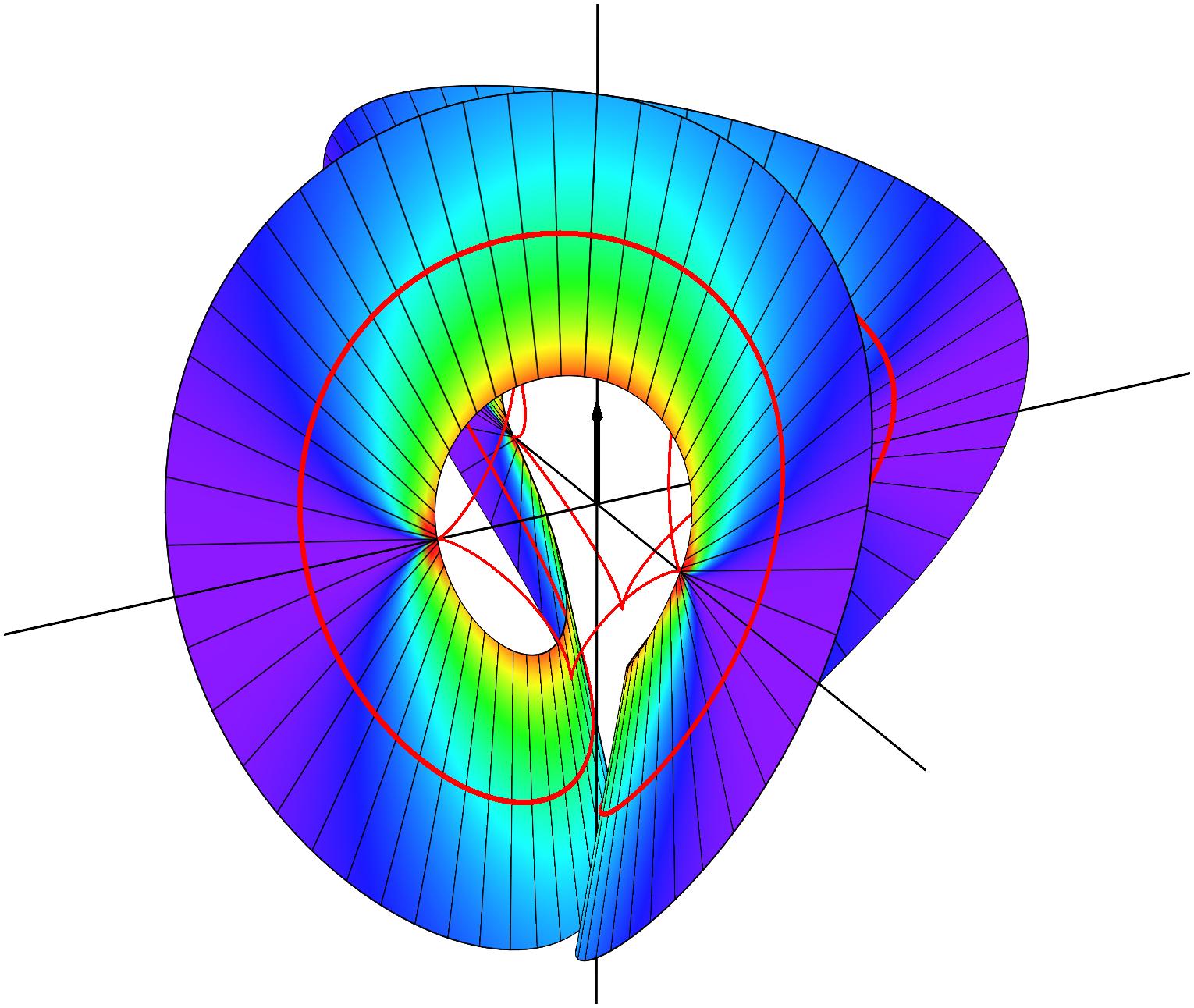
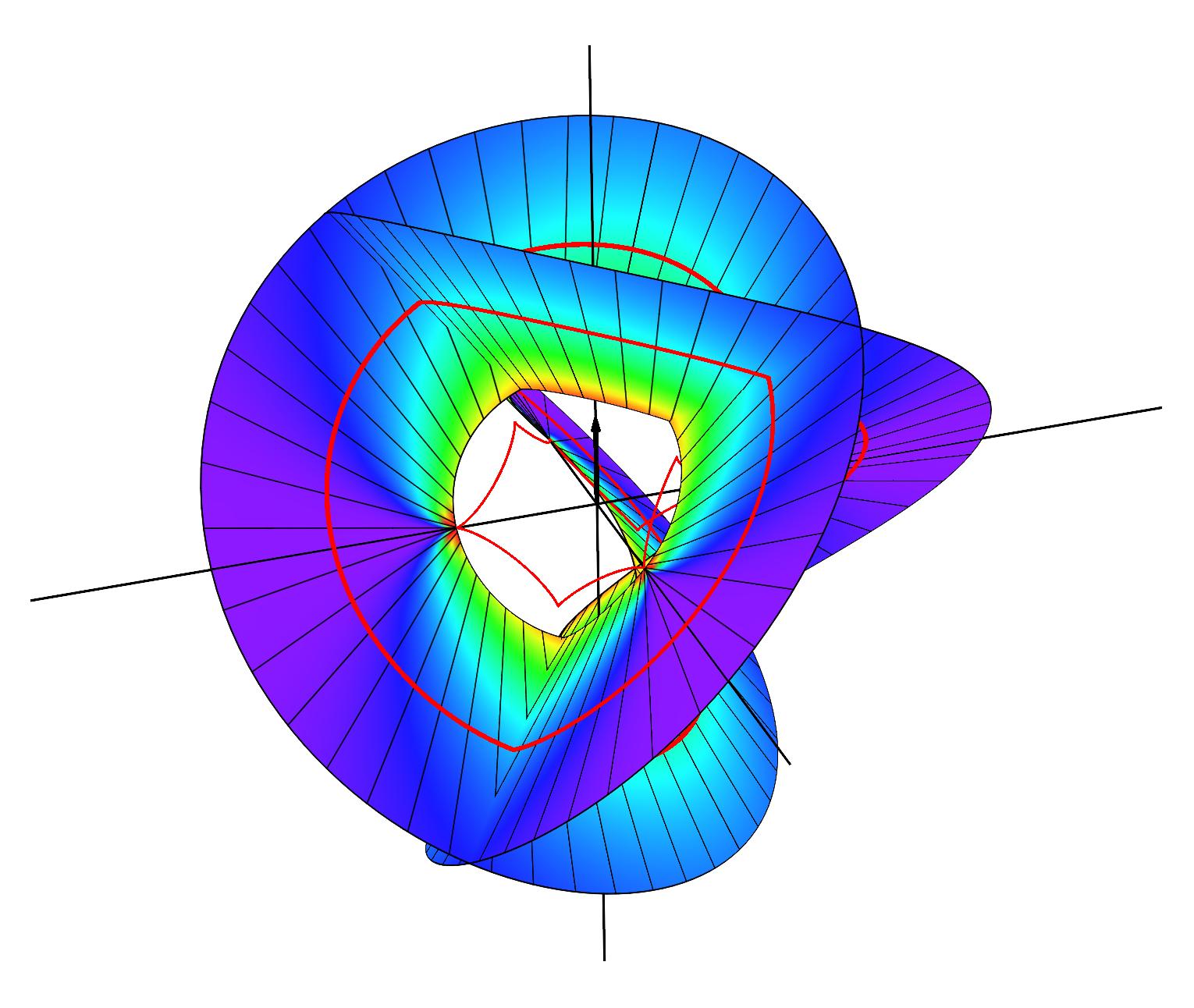
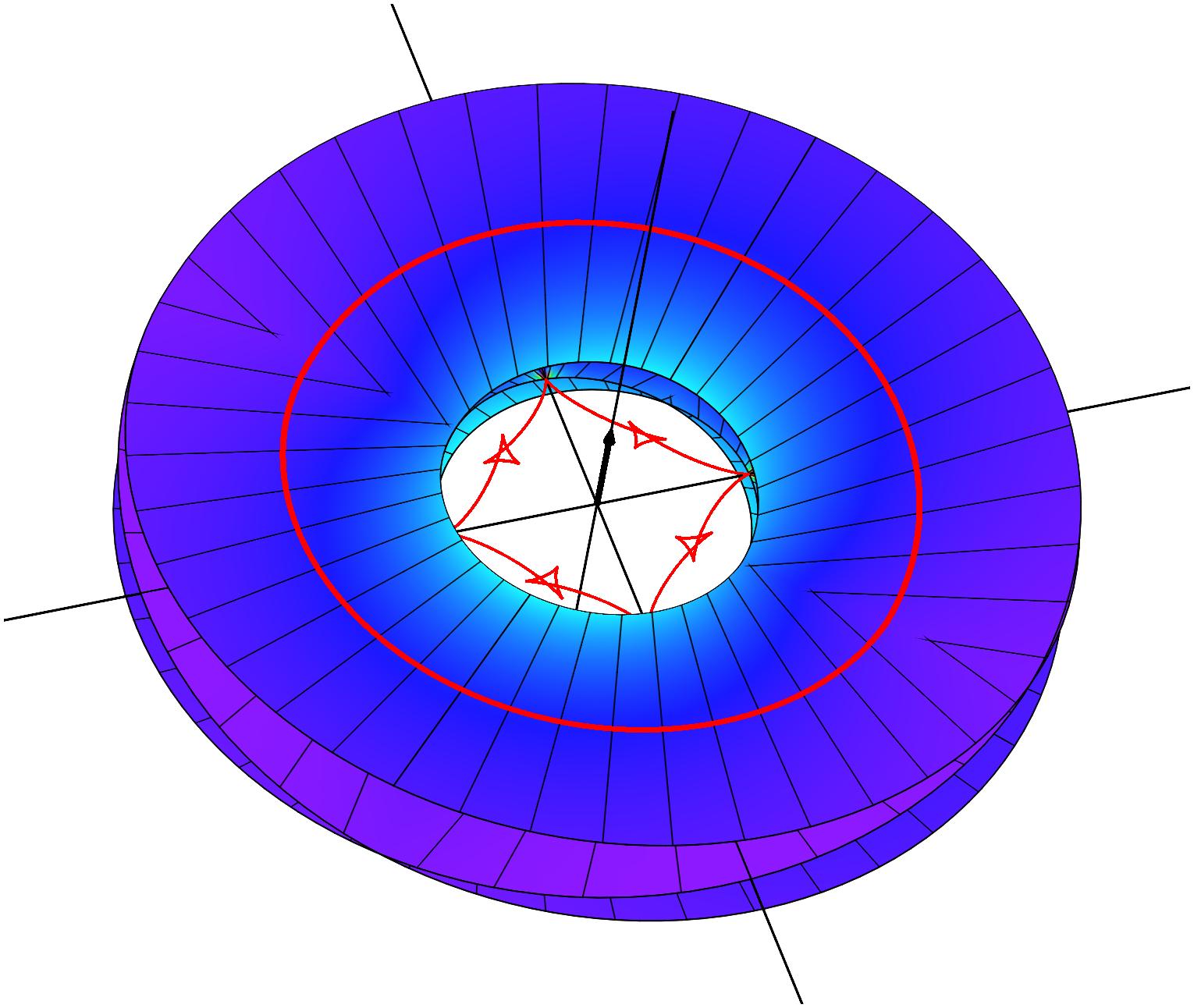
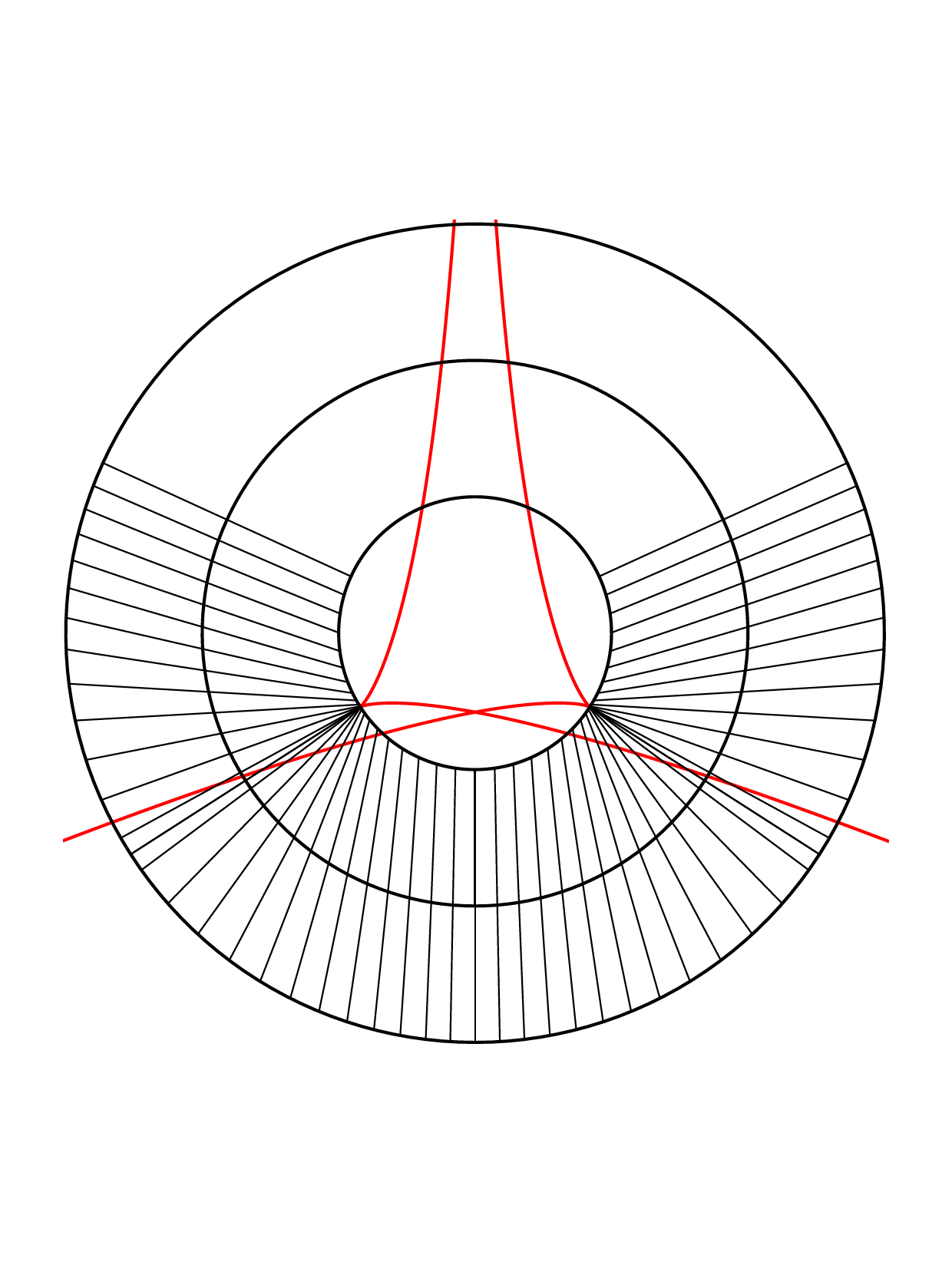
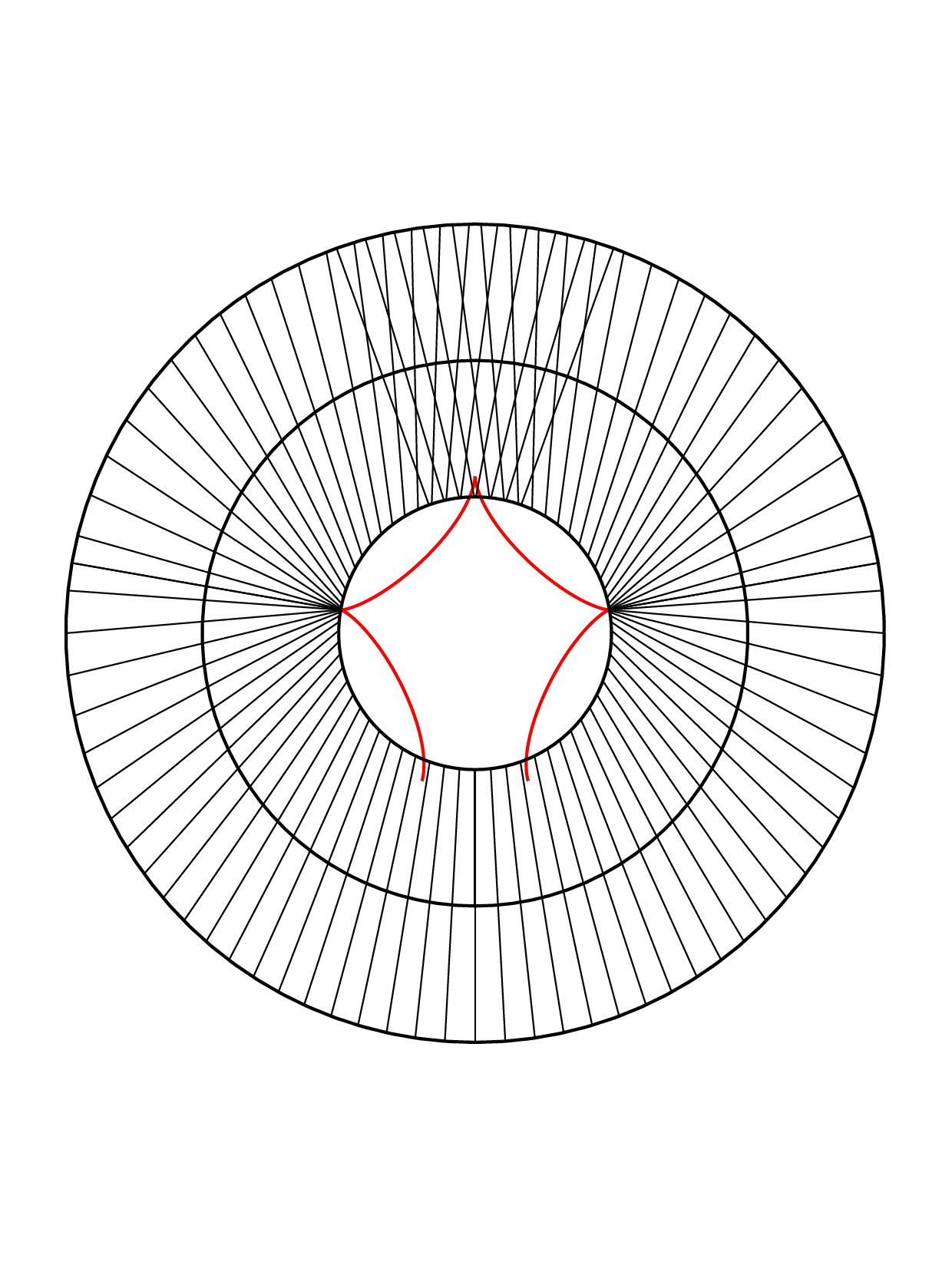
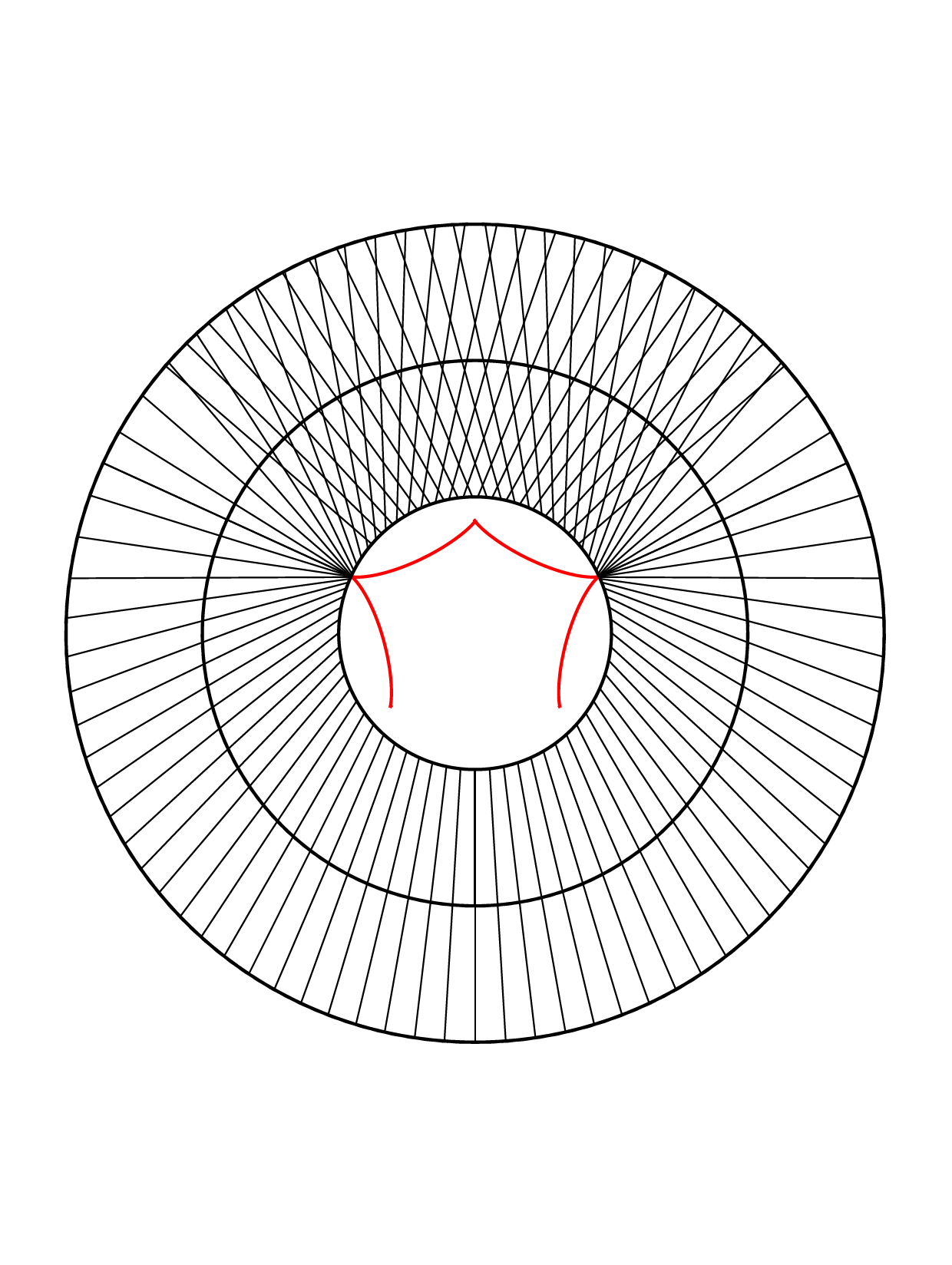
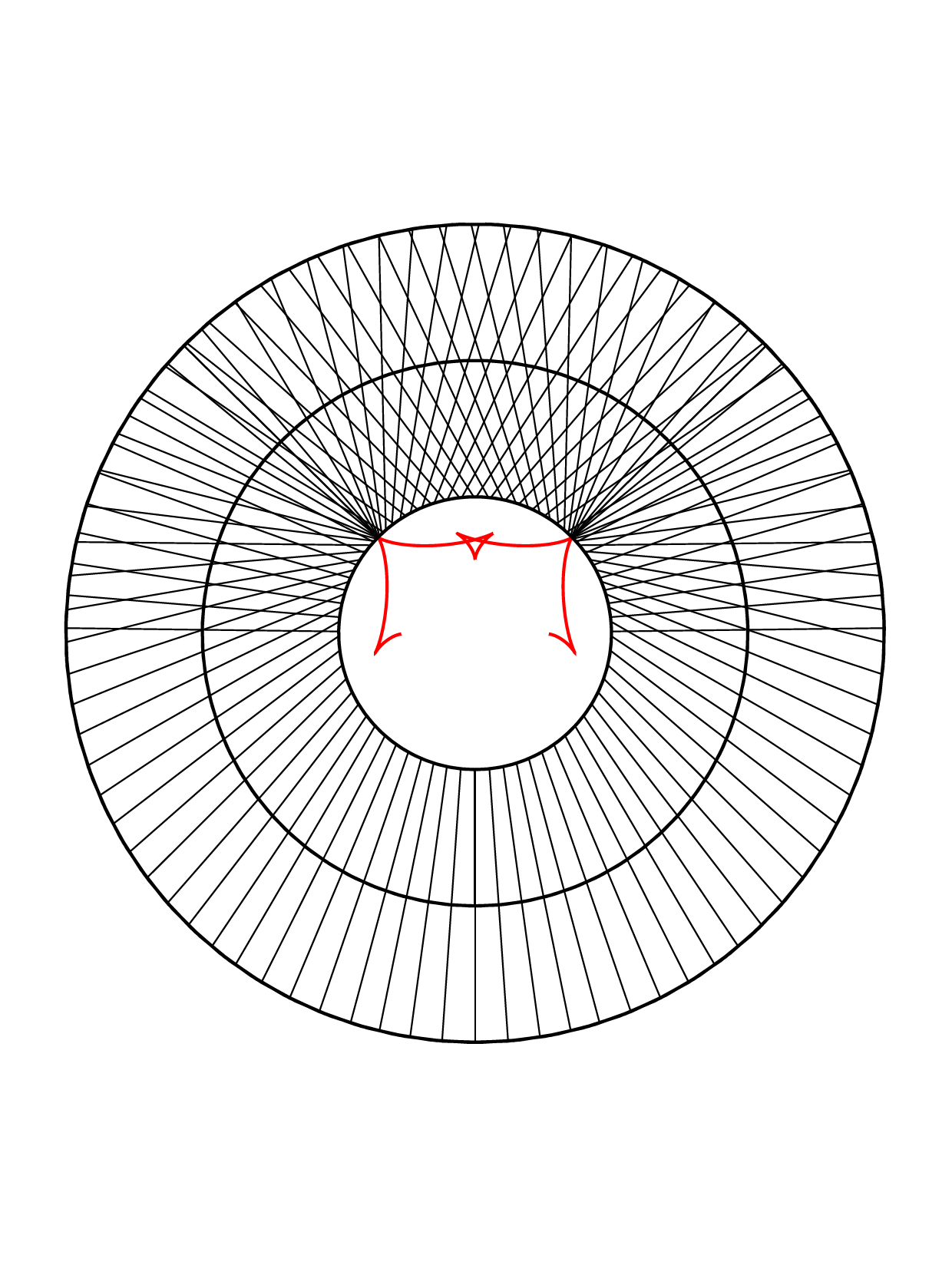
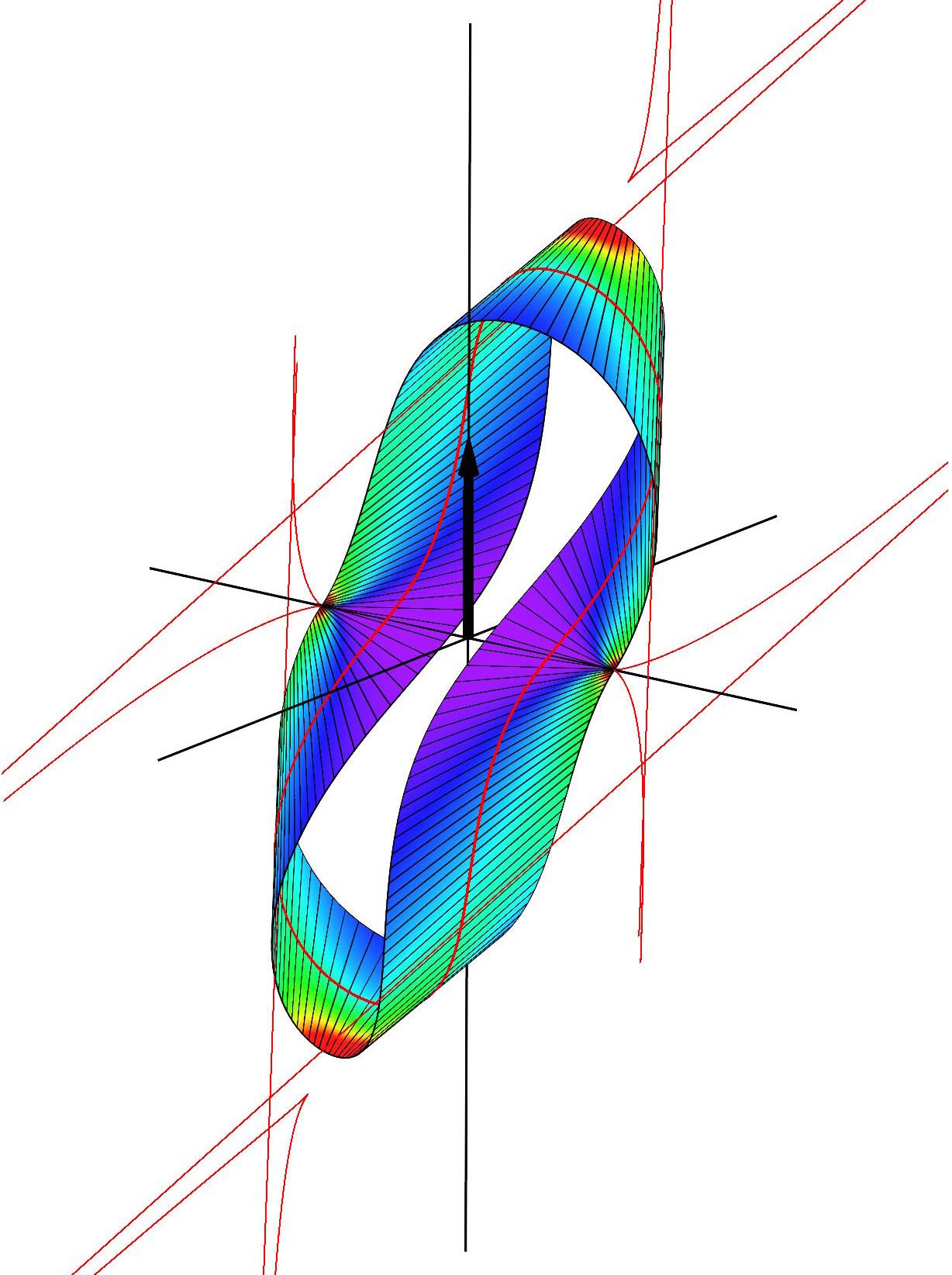
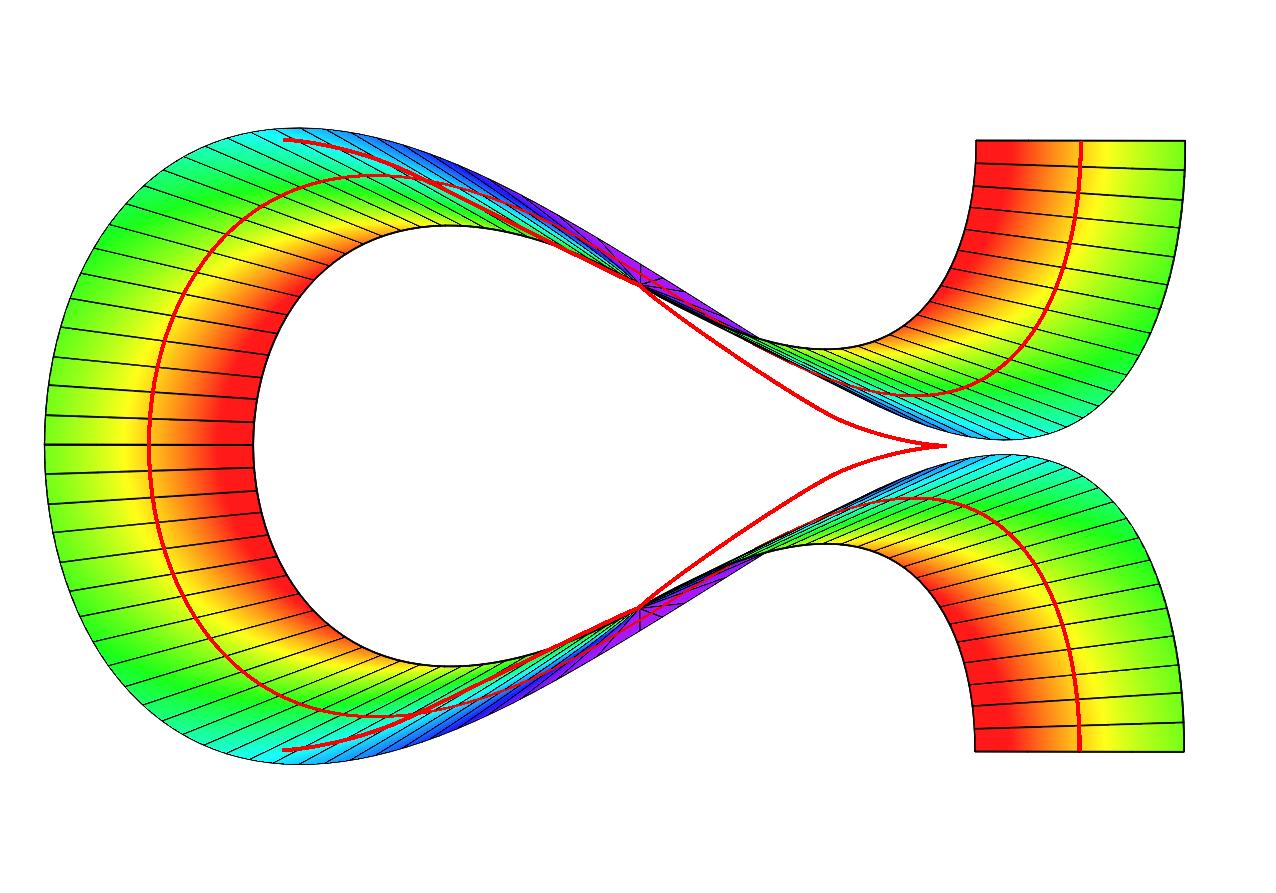

[J. Mech. Phys. Solids 169, 105054 (2022)]
