DIFFaX
is a software written by Mike Treacy and coworkers to calculate X-ray and neutron power
diffraction patterns of stacking disordered materials. There are many examples
in the materials world - every layered material can in principle
have some irregularities in how its layers are stacked. Famous examples include
graphite, molybdenum sulphide, diamond and the MEL/MFI zeolitic system. Our work
focusses mainly on characterising stacking disorder in ice I and several publications
have arisen from a collaboration with Ben Murray
at the University of Leeds.
There are many different ways in which stacking disordered ice (ice Isd)
can be prepared in the lab. Depending on how ice Isd is made and its thermal
history the stacking disorder will be different. This manifests mainly in different
fractions of cubic and hexagonal stacking. The presence of memory effects in the
stacking sequences can introduce additonal complexity.
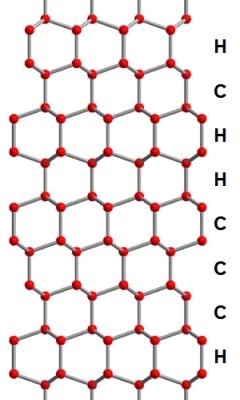
The picture below shows a possible stacking sequence in ice Isd. Hydrogen atoms
have been omitted here for clarity, and "H" and "C" denote hexagonal and cubic stacking,
respectively.
In order to calculate a diffraction pattern DIFFaX requires information about the
atomic structure of the layers, the probabilities of the various types of stacking and
the symmetry relationships between stacked layers. In addition, the calculated pattern
is convolved with peak profile parameters.
DIFFaX itself is not capable of refining the various parameters. This is why we have
"embedded" DIFFaX in a least-square environment within our MCDIFFaX software. MCDIFFaX
uses a simple Monte Carlo based approach to refine the various unknown parameters
including stacking probabilities, lattice constants, zero shift and peak profile
parameters (u, v, w and GL ratio). The programme randomly
suggests a change in one of the parameters, DIFFaX is then asked to calculate the
diffraction pattern and if this leads to an improvement of the fit, the change in
the parameter is accepted. The idea is that this process goes on until the best possible
fit to the experimental data is obtained. The user is required to specify which
parameters should be refined and also the step size of a change. In addition, it
is possible to allow a certain percentage of unfavourable changes in order to avoid
ending up in local minima. Ideally, the step size is chosen quite large initially
and then decreased successively as the fit converges. Similar to Rietveld refinements,
MCDIFFaX requires the user to develop a bit of a "feeling" for the various parameters.
For example, it is advisable to first refine the lattice constants and to then keep
them constant while other parameters are refined.
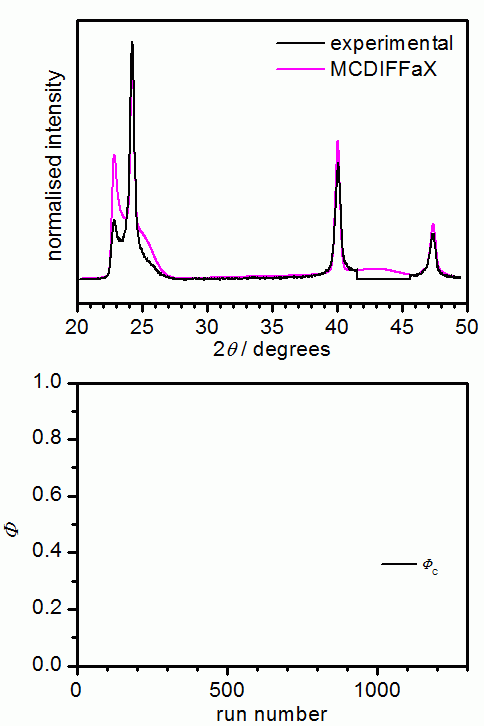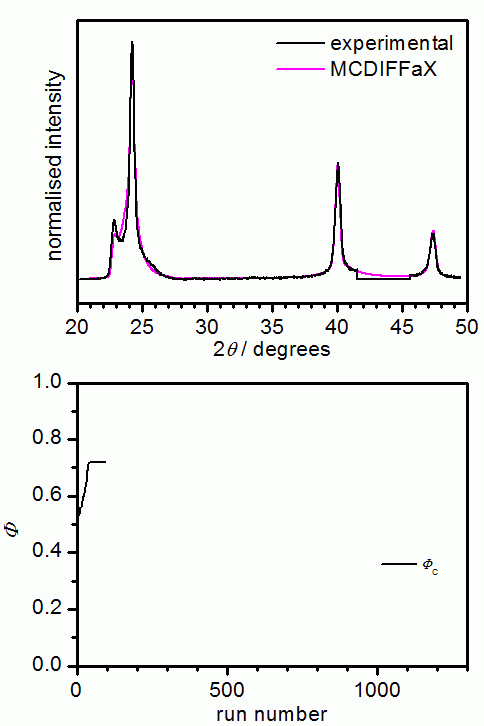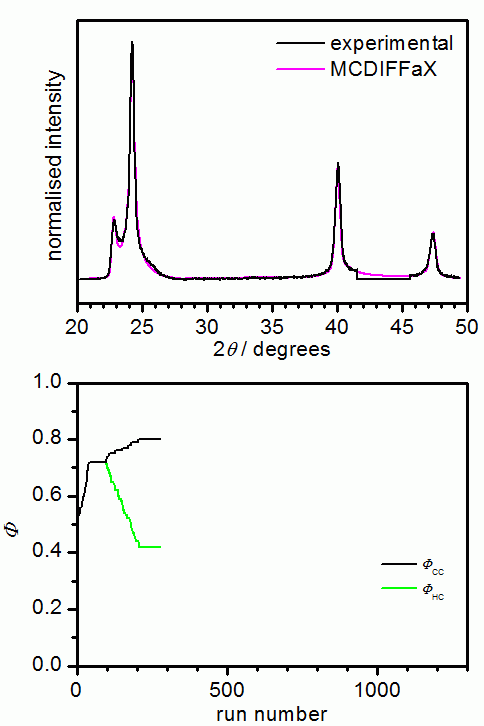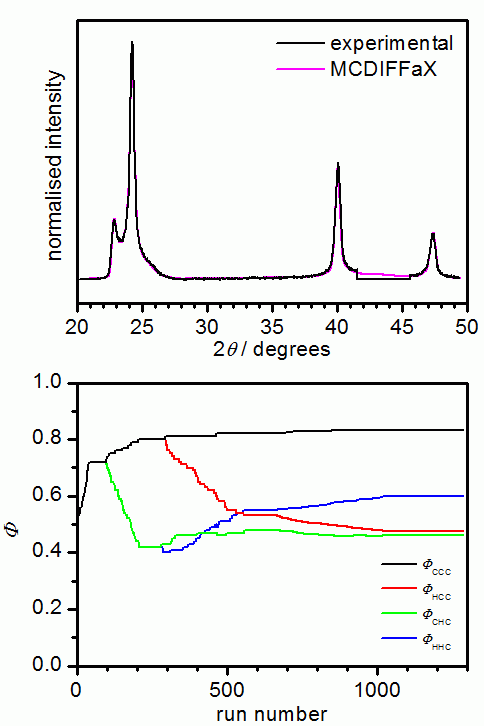
The following picture shows the results from an MCDIFFaX run where all parameters
apart from the stacking probabilities were already known. In our opinion, it is
good practise to initially assume that there are no memory effects present in the
sample. Once the best fit has been obtained, 1st or even 2nd-order memory effects can
be switched on in MCDIFFaX to investigate if this improves the fit to the pattern
further.
MCDIFFaX works only for ice I and diamond in its current version (1.4). However, the long-term aim
is to introduce more flexibility and make it available for download. Any questions or
suggestions - please let me know!
The state of mixing of the two components A and B in binary azeotropic mixtures
has profound consequence on the physicochemical properties. In order to describe
the local molecular environments in binary mixtures in an accessible fashion we
classify them as AA, AB, BA or BB. This is carried out by our LENCA (Local ENvironment ClAssification)
computer program which analyses a given simulation box containing the centre-of-mass
coordinates of the A and B molecules of a binary mixture. The first letter in this classification
scheme indicates the type of molecule under consideration and the second letter
designates the species that dominates the local environment. The condition for
dominating a local environment is that the first coordination shell contains more
of the species in question than the other component. In the unlikely case that the
same numbers of A and B molecules are found in a given local environment LENCA makes a random decision.
To illustrate this kind of analysis we first investigate ideal gas mixtures which
have randomly placed molecules. For these mixtures, there is no defined first coordination shell
and therefore an arbitrary distance was chosen to define the local environment.
In fact, the distance over which the local environments are analysed does not influence
the outcome of our analysis as long as this distance is the same for both species
and all environments. The figure below shows how the local environments change as the
mole fraction of A molecules, xA, increases.
XXX
As expected, only BB environments are found at xA = 0. Upon increasing xA to 0.1
the percentage of BB environments decreases by about 10% since the mole fraction of B
decreases. Owing to the small amounts of A at xA = 0.1 very few BA environments exist.
The local environments of A are initially almost all AB. The chances of finding AA
environments are very small. Upon increasing xA to 0.5 the percentage of BB environments
decreases substantially, and increasing numbers of AB, BA and AA environments are found.
At xA = 0.5 equal percentages of all four environments, i.e. 25%, are found as expected.
Upon further increasing xA, the AA environments begin to dominate and the percentages
of all other local environments tend to zero as xA approaches one. In the figure below, the
changes in environments are shown from the perspective of A molecules only.

