MATH0005 Algebra 1: sets, functions, and permutations

These are the lecture notes for the first part of MATH0005: Algebra 1. The notes are split into numbered sections, one for each teaching video. The notes are very similar to the video content, so you may find it helpful to read the notes before watching the video, or to have a copy of the notes open while you watch the videos.

The aim of this first part of 0005 is to introduce you to some of the key definitions and results from modern algebra that end up being used everywhere in mathematics and everywhere math is used. We’ll cover sets and relations, used whenever we discuss collections of objections and relations among them. We move on to the idea of a function and to key function properties, useful for example whenever we want to compare the size of two sets. Finally we study permutations - ways to rearrange or re-order a set - which are both interesting in their own right and widely applied, for example in linear algebra as you will see later in 0005.

01 Introduction to set theory

Definition of a set

A set is a collection of (mathematical) objects. There is an entire field of mathematics called set theory dedicated to the study of sets and to their use as a foundation for mathematics, but in 0005 we are going to give only an informal introduction to sets and their properties. If you want to know more, take MATH0037 or read any textbook with a title like “Introduction to Set Theory” (I like Derek Goldrei’s Classic Set Theory).

We use curly brackets to denote sets: \(\{1, 2, 3\}\) is the set containing 1, 2, and 3.

Sets are what we use for reasoning about unordered collections of objects, ignoring repetition.

“Unordered” means that we consider \(\{1,2\}\) and \(\{2,1\}\) the same set, “ignoring repetition” means \(\{1,1\} = \{1\}\), for example.

(When we want to take order or repetition into account, we have other mathematical objects to do that, e.g. sequences or multisets).

Elements of a set

The things in a set are called its elements or members. We write \(a \in X\) to mean that \(a\) is an element or member of the set \(X\), and \(a \notin X\) to mean that \(a\) is not an element or member of \(X\).

There is a unique set with no elements, called the empty set and written \(\emptyset\) or \(\{\}\). No matter what \(a\) is, \(a \notin \emptyset\).

There is no restriction on what the elements of a set can be - we allow any kind of mathematical object, including sets themselves. For example

\[\{ \emptyset, 1, \{2\}, \{\{3\}\}\}\]

is a set whose four elements are the empty set, 1, the set containing 2, and the set containing the set containing 3. We can put vectors, functions, matrices, and anything else in a set.

Example. Let \(X = \{1, 2, \{3\}\}\). Then \(1 \in X\), \(0 \notin X\), \(3 \notin X\), \(\{3\} \in X\).

Subsets

We need vocabulary for talking about one set being contained in another.

• \(X\) is a subset of \(Y\), written \(X \subseteq Y\), if and only if every element of \(X\) is also an element of \(Y\).
• \(X\) is equal to \(Y\), written \(X = Y\), if and only if \(X \subseteq Y\) and \(Y \subseteq X\), that is, something is an element of \(X\) if and only if it is an element of \(Y\).
• \(X\) is a proper subset of \(Y\), written \(X \subsetneq Y\), if and only if \(X \subseteq Y\) but \(X \neq Y\).

So \(X\) being a proper subset of \(Y\) means that \(X\) is a subset of \(Y\), but \(Y\) also contains something that \(X\) does not contain.

When \(X\) is not a subset of \(Y\), we write \(X \not\subseteq Y\) (just like we write \(\neq\) for “not equal to”).

Example.

• \(\{0\} \subseteq \{0, 1\}\),
• in fact, \(\{0\} \subsetneq \{0,1\}\)
• \(\{0, 1\} \not\subseteq \{1,2\}\)
• \(\{1, 2, 1\} = \{2, 1\}\)

Why is the last equality true? The only things which can answer “yes” to the question “are you an element of \(\{1,2,1\}\)?” are 1 and 2. The only things which can answer “yes” to the question “are you an element of \(\{1, 2\}\)?” are 1 and 2. So the two sets equal according to our definition.

This is how our definition of set equality captures the idea of sets being unordered collections of objects which disregard repetition.

The definition of subset means that the empty set is a subset of any set. \(\emptyset \subseteq X\) for any set \(X\), because \(\forall x : x \in \emptyset \implies x \in X\) is vacuously true: there’s nothing in \(\emptyset\) which could fail to be in the set \(X\) in order to make \(\emptyset \subseteq X\) false.

Set builder notation

Suppose we have a set \(X\) and a property \(P(x)\) that is true or false for each element \(x\) of \(X\). For example, \(X\) might be the set \(\mathbb{Z} = \{\ldots, -2, -1, 0, 1, 2, \ldots\}\) of all integers and \(P(x)\) might be the property “\(x\) is even”. We write

\[\{ x \in X : P(x) \}\]

for the set of all elements of \(X\) for which the property \(P(x)\) is true. This is called set-builder notation. In our example,

\[\{x \in \mathbb{Z} : x \text{ is even }\}\]

is the set \(\{\ldots, -4, -2, 0, 2, 4, \ldots\}\).

Sometimes you’ll see the alternative notation \(\{x \in X | P(x)\}\) which means exactly the same thing.

02 Set operators

Union, intersection, difference, complement

Let \(A, B\) be sets.

• \(A\cup B\), the union of \(A\) and \(B\), is the set containing the elements of \(A\) and also the elements of \(B\).
• \(A \cap B\), the intersection of \(A\) and \(B\), is the set containing all \(x\) such that \(x \in A\) and \(x \in B\).
• \(A \setminus B\), the set difference of \(A\) and \(B\), is the set of all elements of \(A\) which are not in \(B\).
• If \(A\) is a subset of a set \(\Omega\) then \(A^c\), the complement of \(A\) in \(\Omega\), is the set of all things in \(\Omega\) which are not in A. Thus \(A^c = \Omega\setminus A\)

For example, suppose \(A = \{0,1,2\}, B = \{1,2,3\}, C = \{4\}\). Then:

• \(A \cup B = \{0, 1, 2, 3\}\)
• \(A \cap B = \{1,2\}\)
• \(A \cap C = \emptyset\)
• \(A \setminus B = \{0\}\)
• \(A \setminus C = A\)
• If \(\Omega = \mathbb{N} = \{0, 1, 2, \ldots\}\) then \(A^c\) would be \(\{3, 4, \ldots\}\).

The set \(\mathbb{N} = \{0, 1, 2, \ldots\}\) is called the natural numbers. Some people exclude 0 from \(\mathbb{N}\); in MATH0005 the natural numbers include 0.

It’s typical to draw Venn diagrams to represent set operations. We draw a circle, or a blob, for each set. The elements of the set A are represented by the area inside the circle labelled A. Here are some examples:

Size of a set

The size or cardinality of a set \(X\), written \(|X|\), is the number of distinct elements it has.

Example:

• \(|\{1, 2\}| = 2\),
• \(|\emptyset| = 0\),
• \(|\{1, 2, 1, 3\}| = 3\).

Sets with exactly 0, or 1, or 2, or 3, or… distinct elements are called finite. If a set is not finite it is called infinite.

03 Set algebra

Commutativity and associativity

This section is about the laws that union, intersection, difference, and complement obey. Firstly, it is immediate from the definitions that for all sets \(A\), \(B\):

• \(A \cap B = B \cap A\)
• \(A \cup B = B \cup A\)

This is called the commutativity property for intersection and union.

Next,

For all sets \(A\), \(B\), \(C\):

• \(A \cap (B \cap C) = (A \cap B) \cap C\)
• \(A \cup (B \cup C) = (A \cup B) \cup C\)

which is the associativity property.

Again it is fairly easy to see why this is true: the left hand side of the first equation is everything in \(A\), and in \(B\), and in \(C\), and so is the right hand side.

Associativity tells us means there’s no ambiguity in writing

\[A \cup B \cup C\]

or

\[A \cap B \cap C\]

without any brackets to indicate which union or intersection should be done first. Compare this with

\[1 + 2 + 3\]

There’s no need for brackets because it doesn’t matter whether you do 1+2 first then add 3, or whether you add 1 to the result of 2 + 3. On the other hand \(1 + 2 \times 3\) requires either brackets, or a convention on which operation to do first, before we can make sense of it.

Similarly \(A \cup (B \cap C)\) is different to \((A \cup B) \cap C\) in general, so the brackets are obligatory.

The distributive laws

For any sets \(A\), \(B\), \(C\):

• \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
• \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)

We could prove these results in the standard way we prove equalities of sets: prove the left hand side is \(\subseteq\) the right hand side, then prove the right hand side is \(\subseteq\) the left hand side. But there’s an alternative method similar to truth tables in logic.

The aim is to show that any thing lies in the left hand side if and only if it lies in the right hand side. We can do this case-by-case: any particular element is either in \(A\) or not in \(A\), in \(B\) or not in \(B\), and in \(C\) or not in \(C\). That gives 8 different cases, and in each case we can see whether or not the element belongs to \(A \cup (B\cap C)\) and whether or not it belongs to \((A \cup B) \cap (A \cup C)\).

\(A\)	\(B\)	\(C\)	\(A \cup (B \cap C)\)	\((A \cup B) \cap (A \cup C)\)
no	no	no	no	no
yes	no	no	yes	yes
no	yes	no	no	no
yes	yes	no	yes	yes
no	no	yes	no	no
yes	no	yes	yes	yes
no	yes	yes	yes	yes
yes	yes	yes	yes	yes

Notice that the last two columns are identical.

04 De Morgan’s laws

De Morgan’s laws

Take a look at this Venn diagram:

You can see that the shaded area is exactly the area not in \(A \cup B\), so this is the Venn diagram for \((A \cup B)^c\). Now consider the Venn diagrams for \(A^c\) and \(B^c\):

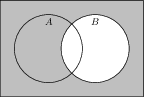
It should be clear that \(A^c \cap B^c = (A \cup B)^c\).
This is a general and useful fact, one of De Morgan’s laws.

Theorem (De Morgan’s Laws).

1. \((A \cup B)^c = A^c \cap B^c\).
2. \((A \cap B)^c = A^c \cup B^c\).

Proof: To show that two sets \(X\) and \(Y\) are equal we can show that \(X \subseteq Y\) and \(Y \subseteq X\). This is how we will prove these two results.

1. If \(x \in (A \cup B)^c\) then \(x \notin A \cup B\), so \(x \notin A\) (and therefore \(x \in A^c\)) and \(x \notin B\) (and \(x \in B^c\)). Therefore \(x \in A^c \cap B^c\). We’ve shown every element of \((A \cup B)^c\) is also an element of \(A^c \cap B^c\), so \((A \cup B)^c \subseteq A^c \cap B^c\). Conversely if \(x \in A^c \cap B^c\) then \(x \notin A\) and \(x \notin B\), so \(x \notin A \cup B\) or equivalently \(x \in (A\cup B)^c\). We’ve shown every element of \(A^c \cap B^c\) is also an element of \((A \cup B)^c\), so \(A^c \cap B^c \subseteq (A\cup B)^c\). Since we have shown \(A^c \cap B^c \subseteq (A\cup B)^c\) and \((A\cup B)^c \subseteq A^c \cap B^c\), the two sets are equal.
2. More concisely: an element \(x\) lies in \((A\cap B)^c\) if and only if it is not in \(A \cap B\), if and only if either \(x \notin A\) or \(x \notin B\), if and only if \(x \in A^c\) or \(x \in B^c\), if and only if \(x \in A^c \cup B^c\). The sets \((A\cap B)^c\) and \(A^c \cup B^c\) have the same elements, so they are equal.

---

De Morgan’s laws also work for unions and intersections of more than two sets: for any sets \(A_1, A_2, \ldots\) we have

• \((A_1 \cup A_2 \cup \cdots)^c = A_1^c \cap A_2^c \cap \cdots\)
• \((A_1 \cap A_2 \cap \cdots)^c = A_1^c \cup A_2^c \cup \cdots\)

Complement of a complement

Let’s record one more fact about sets and complements: for any set \(X\) which is a subset of another set \(\Omega\), if the complement of the complement of \(X\) in \(\Omega\) is \(X\) again. In symbols, \(X^{cc} = X\). This is because \(x \in X^{cc}\) if and only if \(x\) is not in \(X^c\), if and only if \(x\) is not not in \(X\), if and only if \(x\) is in \(X\).

Applying De Morgan

Five housemates share a fridge. They want to fit locks to the fridge subject to two conditions:

1. no two housemates can unlock every fridge lock
2. any three housemates can unlock every fridge lock

Is it possible? How many keys do they need? How should they be distributed?

They fit some number of locks to the fridge door. Each key works in one lock only, but they can have as many copies of each key as they want.

Let’s set up some notation.

• \(\Omega =\) set of all locks that they use.
• \(K_i\) = locks that housemate \(i\) has the key to, \(1\leq i \leq h\)
• \(N_i = K_i^c = \Omega \setminus K_i\), the locks that housemate \(i\) doesn’t have the key to.

Translating condition 1 above into the language of sets, for all \(i\), \(j\) we have \(K_i \cup K_j \neq \Omega\).

If we take complements of both sides, we get that for all \(i,j\), \((K_i \cup K_j)^c \neq \Omega^c\). Using De Morgan’s laws, this means \(N_i \cap N_j \neq \emptyset\).

Translating condition 2 into set language, for all distinct \(i, j, k\), \(K_i\cup K_j \cup K_k=\Omega\).

Taking complements of both sides, this means that for all distinct \(i, j, k\) we have \((K_i \cup K_j \cup K_k)^c = \emptyset\). Using De Morgan’s laws, \(N_i \cap N_j \cap N_k = \emptyset\).

This points us to a solution. If \(i\), \(j\) are distinct then \(N_i\) and \(N_j\) have an element in common as \(N_i \cap N_j \neq \emptyset\), but this doesn’t belong to any other \(N_k\) since \(N_i \cap N_j \cap N_k =\emptyset\). So we need one lock \(l_{ij}\) for each unordered pair of distinct integers \(i\) and \(j\) between \(1\) and \(h\) - unordered means that \(l_{12} = l_{21}\), for example. We can then allocate housemate \(i\) the keys to all locks \(l_{rs}\) with \(r,s \neq i\).

This obeys condition 1, because for any \(i, j\), neither housemate \(i\) nor housemate \(j\) has the ley to \(l_{ij}\), so \(K_i \cup K_j \neq \Omega\).

It also obeys condition 2, because if \(i,j,k\) are all different then given any lock \(l_{rs} \in \Omega\), either

• \(l_{rs} \neq l_{ij}\) (in which case \(l_{rs} \in K_i \cup K_j\)), or
• \(l_{rs} = l_{ij}\) (in which case \(l_{rs} \in K_k\), as \(k\) is not \(i\) or \(j\))

In either case, at least one of the three housemates can open the lock.

05 Cartesian products

Ordered pairs

When we want to use coordinates to talk about points in the plane, we often do this with pairs of real numbers \((x,y)\): \(x\) tells you how far across to go and \(y\) how far up. The key properties of these pairs \((x, y)\) is that \((x,y) = (z,w)\) if and only if \(x=z\) and \(y=w\). A construction with this property is called an ordered pair, and we can form ordered pairs with elements from any two sets - not just for real numbers.

Cartesian products

The Cartesian product of two sets \(A\) and \(B\), written \(A\times B\), is the set of all ordered pairs in which the first element belongs to \(A\) and the second belongs to \(B\).

\[A \times B = \{(a, b) : a \in A, b \in B\}\]

Notice that the size of \(A\times B\) is the size of \(A\) times the size of \(B\), that is, \(|A \times B| = |A| |B|\).

Example. \(\{1,2\} \times \{2,3\} = \{(1,2), (1,3), (2,2), (2,3)\}\).

Of course we produce ordered triples \((a, b, c)\) as well, and ordered quadruples, and so on.

06 Introduction to functions

Definition of function, domain, codomain

Informally, given sets \(X\) and \(Y\), a function or map \(f\) from \(X\) to \(Y\) is a definite rule which associates to each \(x \in X\) an element \(f(x) \in Y\).

We write \(f:X \to Y\) to mean that \(f\) is a function from \(X\) to \(Y\). \(X\) is called the domain of \(f\) and \(Y\) is called the codomain of \(f\).

We refer to the element \(f(x)\) of \(Y\) as being the “output” or “value” of \(f\) when it is given the “input” or “argument” \(x\).

This might seem vague: what is a definite rule?, what does associates mean?, when are two functions the equal? - should we insist the rule is the same, or just that the input-output relationship is the same?

The formal definition of a function is:

Definition: A function consists of a domain \(X\), a codomain \(Y\), and a subset \(f \subseteq X\times Y\) containing exactly one pair \((x, y)\) for each \(x \in X\). We write \(f(x)\) for the unique element of \(Y\) such that \((x,f(x))\) is in \(f\).

In other words, the formal definition of a function is its set of (input, output) pairs.

Example: the function \(f:\mathbb{N} \to \mathbb{N}\) such that \(f(x) = x+1\) would correspond to \(\{ (0, 1), (1, 2), (2, 3) \ldots\} \subseteq \mathbb{N} \times \mathbb{N}\)

We won’t use the formal definition in 0005.

When are two functions equal?

Two functions \(f\) and \(g\) are equal if and only if

• they have the same domain, say \(X\), and
• they have the same codomain, and
• \(f(x)=g(x)\) for every \(x \in X\).

They really must have the same domain and same codomain to be equal, according to this definition.

Example: \(f, g : \{0, 1\} \to \{0, 1\}\). \(f(x)=x^2\). \(g(x) = x\). Are they equal?

(the answer is yes - they have the same domain, same codomain, and the same output for every input from the domain).

The identity function

For any set \(X\), the identity function \(\operatorname{id}: X \to X\) is defined by \(\operatorname{id}(x)=x\).

07 Function composition

Definition of function composition

Suppose you have two functions \(f: X \to Y\) and \(g : Y \to Z\):

\[X \stackrel{f}{\to} Y \stackrel{g}{\to} Z\]

Then you can make a new function \(X \to Z\) whose rule is “do \(f\), then do \(g\)”.

Definition: let \(f:X\to Y\) and \(g : Y \to Z\). The composition of \(g\) and \(f\), written \(g \circ f\) or \(gf\), is the function \(g\circ f : X \to Z\) with the rule \((g\circ f)(x) = g(f(x))\).

This makes sense because \(f(x)\) is an element of \(Y\) and \(g\) has domain \(Y\) so we can use any element of \(Y\) as an input to \(g\).

It’s important to remember that \(g \circ f\) is the function whose rule is “do \(f\), then do \(g\)”. Be careful to get that the right way round.

Associativity

Functions \(f\) and \(g\) such that the codomain of \(f\) equals the domain of \(g\) are called composable.

Composition has an important property called associativity. Suppose \(f\) and \(g\), and \(g\) and \(h\), are composable:

\[X \stackrel f\to Y \stackrel g\to Z \stackrel h \to W\]

It seems there are two different ways to compose them: you could first compose \(f\) and \(g\), then compose the result with \(h\), or you could compose \(g\) with \(h\) and then compose the result with \(f\). But they both give the same result.

Lemma: let \(f: X \to Y, g: Y \to Z, h : Z \to W\). Then \(h\circ (g \circ f) = (h \circ g) \circ f\).

Proof: Both \(h\circ(g\circ f)\) and \((h\circ g) \circ f\) have the same domain \(X\), same codomain \(W\), and same rule \(x \mapsto h(g(f(x)))\).

This property is called associativity: we discussed the same thing for unions and intersections earlier. Again, it means that a composition like

\[f \circ g \circ h \circ k \circ \cdots \circ z\]

doesn’t require any brackets to make it unambiguous.

Composition with the identity function

Lastly, let’s make an observation about identity functions and composition: if \(f:X \to Y\) then

\[f = f \circ \operatorname{id}_X = \operatorname{id}_Y \circ f\]

since for example \((f\circ \operatorname{id}_X)(x) = f(\operatorname{id}_X(x)) = f(x)\), for any \(x \in X\).

08 Function properties

Image of a function

Let \(f: X \to Y\). Then the image of \(f\) is \(\operatorname{im}(f) = \{f(x) : x \in X\}\).

Don’t confuse codomain and image. \(Y\) is the codomain of \(f\). The image \(\operatorname{im} f\) is a subset of \(Y\), but it need not equal \(Y\).

Injection, surjection, bijection

The three most important function properties:

• \(f\) is injective or one-to-one if and only if for all \(a,b \in X\), if \(f(a)=f(b)\) then \(a=b\).
• \(f\) is surjective or onto if and only if for all \(y \in Y\) there is at least one \(x \in X\) such that \(f(x)=y\).
• \(f\) is a bijection if and only if it is injective and surjective.

Another way to write the definition of surjective would be that a function is surjective if and only if its image equals its codomain.

As an example, here’s a picture of a function \(f: \{1,2,3,4,5,6\} \to \{1,2,3,4,5\}\). I have drawn an arrow from \(x\) to \(f(x)\) for each \(x\) in the domain of \(f\).

\(f\) is not onto because \(\operatorname{im}(f)\) is a proper subset of the codomain (\(\operatorname{im}(f)\) doesn’t contain 4 but the codomain does). Also \(f\) is not one-to-one, because \(f(1) = f(2)\) but \(1 \neq 2\).

More examples:

• \(f : \mathbb{R} \to \mathbb{R}, f(x)=x^2\). It isn’t injective as \(f(-1)=f(1)\) and it isn’t surjective as \(-1\) is in the codomain, but there’s no element \(x\) in the domain such that \(f(x)=-1\).
• \(g: \mathbb{R} \to [0, \infty), g(x)=x^2\). This is not injective for the same reason as before, but this time it is surjective: for each \(y \geq 0\) we can find an element of the domain which \(g\) sends to \(y\): for example. \(g(\sqrt{y}) = 0\).
• \(h : [0, \infty) \to \mathbb{R}, h(x)=x^2\). Not surjective, for the same reason \(f\) isn’t surjective (the codomain contains negative numbers, but the image doesn’t contain any negative numbers, so the image doesn’t equal the codomain). But \(h\) is injective: if \(x\) and \(y\) are in the domain of \(h\) and \(h(x)=h(y)\) then \(x^2=y^2\), so \(x = \pm y\). Since elements of the domain of \(h\) are nonnegative, it must be that \(x = y\).
• \(j : (-\infty, 0] \to [0, \infty), j(x) = x^2\). This is injective (for a similar reason to \(h\)) and surjective (for a similar reason to \(g\)), so it is a bijection.

This illustrates an important point: when you talk about a function you must specify its domain and codomain (as well as the rule, of course).

Bijections and sizes of sets

How do we know when two sets have the same size? If you see an alien creature with an apple in each of its hundreds of hands you know it has the same number of apples as it does hands, even if you haven’t counted either the apples or the hands.

You know that because you can pair each apple with the hand holding it. Every apple is held by one hand, and every hand holds one apple.

Suppose there is a bijection \(f\) between two sets \(X\) and \(Y\). This gives us a way to pair up elements of \(X\) and elements of \(Y\) such that every element of \(X\) is paired with exactly one element of \(Y\).

Consider the pairs \((x, f(x))\) for \(x\) in \(X\). Every element of \(Y\) appears in exactly one of these pairs (at least one pair because \(f\) is onto, at most one pair because \(f\) is one-one). So a bijection pairs up each element of \(X\) with a unique element \(f(x)\) of \(Y\).

The picture is an illustration of a bijection \(f:\{1,2,3\}\to \{a,b,c\}\). If we pair each element \(x\) of the domain with its image \(f(x)\) we get the pairs \((1, c), (2, b), (3, a)\). Because \(f\) is a bijection, every element of the domain is paired with exactly one element of the domain and every element of the codomain is paired with exactly one element of the domain.

All this leads us to make this definition: two sets have the same size (or the same cardinality)if and only if there is a bijection between them.

This definition works even for infinite sets - though it sometimes provides some counterintuitive results. The sets \(\mathbb{Z}\) and \(2 \mathbb{Z} = \{\ldots -4, -2, 0, 2, 4, 6, \ldots\}\) have the same size since there is a bijection

\[\begin{align*} f : \mathbb{Z} &\to 2 \mathbb{Z} \\ f(z) &= 2z \end{align*}\]

09 Invertibility

Definition: let \(f:X \to Y\).

• a left-inverse to \(f\) is a function \(g: Y \to X\) such that \(g\circ f=\operatorname{id}_X\)
• a right-inverse to \(f\) is a function \(h : Y \to X\) such that \(f\circ h=\operatorname{id}_Y\)
• an inverse (or a two-sided inverse) to \(f\) is a function \(k:Y \to X\) which is a left and a right inverse to \(f\).

Notice that if \(g\) is left-inverse to \(f\) then \(f\) is right-inverse to \(g\). A function can have more than one left-inverse, or more than one right-inverse: you will investigate this further in exercises.

The idea is that a left-inverse “undoes” what its right-inverse “does”, in the sense that if you have a function \(f\) with a left-inverse \(g\), and you start with \(x \in X\) and “do” \(f\) to get to \(f(x) \in Y\), then \(g(f(x)) = x\) so \(g\) undoes what \(f\) did and gets you back to the element \(x\) you started with.

Examples:

• \(f: \mathbb{R} \to [0, \infty), f(x)=x^2\) has a right-inverse \(g: [0, \infty) \to \mathbb{R}, g(x)=\sqrt{x}\). \(f(g(x)) = x\) for all \(x \in [0, \infty)\). This is not a left-inverse.
• This function \(f\) does not have a left inverse. Suppose \(h\) is left-inverse to \(f\), so that \(hf=id_\mathbb{R}\). Then \(h(f(-1))=-1\), so \(h(1)=-1\). Similarly \(h(f(1))=1\), so \(h(1) = 1\). Impossible! (The problem is that \(f\) isn’t one-to-one.)
• The function \(g\) has a left-inverse, \(f\). But it does not have a right-inverse. If \(g\circ h = id_{\mathbb{R}}\) then \(g(h(-1)) = -1\) so \(g(h(-1)) = -1\). But there’s no element of \([0, \infty)\) that \(g\) takes to \(-1\). (This time the problem is that \(g\) isn’t onto.)

10 When is a function invertible?

Inverses and function properties

Here is the connexion between function properties and invertibility.

Theorem: Let \(f:X \to Y\), and assume \(X \neq \emptyset\). Then

1. \(f\) has a left-inverse if and only if it is injective
2. \(f\) has a right-inverse if and only if it is surjective
3. \(f\) is invertible if and only if it is bijective

Proof:

1. • ONLY IF. Let \(g\) be left-inverse to \(f\), so \(g\circ f=\operatorname{id}_X\). Suppose \(f(a)=f(b)\). Then applying \(g\) to both sides, \(g(f(a))=g(f(b))\), so \(a=b\).
   • IF. (draw a picture to illustrate construction) Let \(f\) be injective. Choose any \(x_0\) in the domain of \(f\). Define \(g:Y \to X\) as follows. Each \(y\) in \(Y\) is either in the image of \(f\) or not. If \(y\) is in the image of \(f\), it equals \(f(x)\) for a unique \(x\) in \(X\) (uniqueness is because of the injectivity of \(f\)), so define \(g(y)=x\). If \(y\) is not in the image of \(f\), define \(g(y)=x_0\). Clearly \(g\circ f= \operatorname{id}_X\).
2. • IF. Suppose \(f\) has a right inverse \(g\), so \(f \circ g = \operatorname{id}_Y\). If \(y \in Y\) then \(f(g(y)) = \operatorname{id}_Y(y) = y\), so \(y \in \operatorname{im}(f)\). Every element of \(Y\) is therefore in the image of \(f\), so \(f\) is onto.
   • ONLY IF. Suppose \(f\) is surjective. Let \(y \in Y\). Then \(y\) is in the image of \(f\), so we can choose an element \(g(y) \in X\) such that \(f(g(y)) = y\). This defines a function \(g : Y \to X\) which is evidently a right-inverse to \(f\).
3. If \(f\) has a left inverse and a right inverse, it is injective (by part 1 of this theorem) and surjective (by part 2), so is a bijection. Conversely if \(f\) is a bijection it has a left inverse \(g:Y\to X\) and a right inverse \(h:Y\to X\) by part 1 and part 2 again. But “invertible” required a single function which was both a left and a right inverse. We must show \(g=h\): \[\begin{align*} g &= g\circ \operatorname{id}_Y \\ &= g \circ (f \circ h) & \text{as } fh = \operatorname{id}_Y \\ &= (g\circ f) \circ h & \text{associativity} \\ &= \operatorname{id}_X \circ h & \text{as } gf=\operatorname{id}_X \\ &= h \end{align*}\] so \(g=h\) is an inverse of \(f\).

The diagram illustrates the construction in part 1 of the theorem. Arrows from left to right show where \(f\) sends each element of \(X\). Arrows from right to left show where the left inverse \(g\) we have constructed sends each element of \(Y\).

Notation: if \(f\) is invertible, we write \(f^{-1}\) for THE inverse of \(f\).

(there’s only one inverse, because if \(g\) and \(h\) are inverses to \(f\) then by the argument in part 3 above, \(g=h\).)

Inverses are important to us. You’ll see the following result in a lot of contexts.

Inverse of a composition

Theorem: If \(f :X \to Y\) and \(g:Y \to Z\) are invertible then so is \(g\circ f\), and \((g\circ f)^{-1} = f^{-1}\circ g^{-1}\).

Proof: you can check that \(f^{-1}\circ g^{-1}\) is a left- and right- inverse to \(g\circ f\).

It is important to get this the right way round. The inverse of \(g\circ f\) is not normally \(g^{-1} \circ f^{-1}\), indeed this composition may not even make sense.

The correct result is easy to remember when you think about getting dressed. Each morning you put on your socks, then you put on your shoes: if \(k\) is the put-on-socks function and \(h\) is the put-on-shoes function then you apply the function \(h \circ k\) to your feet. The inverse of this is taking off your shoes, then taking off your socks: \(k^{-1} \circ h^{-1}\). Not the other way round - it’s not even (normally) possible to take off your socks, then take off your shoes, just as it is not normally possible to form the composition \(g^{-1}\circ f^{-1}\) in the context of the theorem above.

A similar result applies when you compose more than two invertible functions: if \(f_1, f_2, \ldots, f_n\) are invertible and if the composition \[f_1\circ \cdots \circ f_n\] makes sense, it is also invertible and its inverse is

\[f_n^{-1} \circ \cdots \circ f_1^{-1}.\]

11 Relations

Definition of a relation

Informally, a relation on a set \(X\) is a property of an ordered pair of elements of \(X\) that could be true or false.

You know many of these.

• \(\leq\) is a relation on \(\mathbb{R}\). For any ordered pair \((x,y)\) of real numbers, \(x \leq y\) is either true or false.
• \(\neq\) is a relation on \(\mathbb{Z}\). For any ordered pair \((x, y)\) of integers, \(x \neq y\) is either true or false.
• The parity of an integer is whether it is odd or even. \(x \sim y\) if and only if \(x\) and \(y\) have the same parity is a relation on \(\mathbb{Z}\) - for example, \(-2 \sim 48\) but it is not true that \(0 \sim 3\). When \(a \sim b\) is false, we write \(a \nsim b\).
• Two silly examples: let \(X\) be any set. There is an empty relation \(\sim_e\) on \(X\) such that \(x \sim_e y\) is never true for any \(x, y \in X\), and a universal relation \(\sim_u\) such that \(x \sim_u y\) is always true for any \(x, y \in X\).

Just as for functions, there is a formal definition of a relation…

Formal definition: a relation \(\sim\) on a set \(X\) is a subset of \(X\times X\). We write \(x\sim y\) to mean \((x, y) \in \sim\).

…which we won’t use in 0005. But it is good to know such a thing exists, because it gets us out of having to say what a “property that could be true or false” really is.

Congruence modulo n

This is a very important example of a relation on the set \(\mathbb{Z}\) of integers, which we will use later in 0005 and which occurs throughout mathematics.

For each integer \(n \neq 0\), there is a relation on \(\mathbb{Z}\) called congruence modulo \(n\) (or just “congruence mod n”, for short). Two integers \(x\) and \(y\) are congruent modulo \(n\) if and only if \(x-y\) is divisible by \(n\).

There is a special notation for this relation: we write

\[x \equiv y \mod n\]

to mean that \(x\) and \(y\) are congruent modulo \(n\).

Examples:

• \(3\) and \(-7\) are congruent modulo 2, as \(3 - (-7) = 10\) is divisible by 2 (in fact, congruence modulo 2 is the same as the last example relation above). But \(3\) and \(8\) are not congruent modulo 2 because \(3- 8=-5\) isn’t a multiple of \(2\).
• \(3\) and \(-7\) are congruent modulo \(5\) as \(3 - (-7)=10\) is divisible by \(5\). But \(12\) and \(3\) are not congruent modulo \(5\) because \(12-3\) isn’t divisible by \(5\)

12 Relation properties

Reflexive, symmetric, transitive

Let \(\sim\) be a relation on a set \(X\).

• \(\sim\) is reflexive (R) if and only if \(\forall x \in X : x \sim x\).
• \(\sim\) is symmetric (S) if and only if \(\forall x, y \in X: x \sim y \implies y \sim x\).
• \(\sim\) is transitive (T) if and only if \(\forall x,y,z \in X: x\sim y\) and \(y \sim z\) implies \(x \sim z\).

\(\sim\) is an equivalence relation if and only if it has all three properties (R), (S), and (T).

There’s no restriction or hidden assumptions on \(x,y,z\), like “they have to be distinct” or something like that. \(\sim\) is transitive if and only if for every \(x,y,z\) it is true that if \(x\sim y\) and \(y\sim z\) then \(x \sim z\).

Here is a table of examples. The R, S, T, E columns contain y if the relation is reflexive, symmetric, transitive, or an equivalence relation, otherwise they contain n.

relation and set	R	S	T	E
\(\leq, \mathbb{R}\)	y	no, \(1\leq 2, 2 \nleq 1\)	y	n
\(<, \mathbb{R}\)	n	n	y	n
Empty relation, \(\mathbb{Z}\)	n	y	y	n
Empty relation, \(\emptyset\)	y	y	y	y
a~b iff a-b even, \(\mathbb{Z}\)	y	y	y	y
\(\neq, \mathbb{N}\)	n	y	n	n

Definition of equivalence class

The last relation in the table could be expressed in a different way: two integers are related if and only if they have the same parity, that is, they’re both odd or they’re both even. The relation comes from splitting up \(\mathbb{Z}\) into two subsets with no elements in common, the set of odd integers and the set of even integers. In fact every equivalence relation arises from splitting a set up into some number of parts, as we’ll now investigate.

To do this we need the notion of an equivalence class.

Let \(\sim\) be an equivalence relation on \(X\) and \(x \in X\). The equivalence class of \(x\) is \[\{ a \in X : a \sim x\}.\] We write \([x]_{\sim }\) or just \([x]\) for the equivalence class of \(x\).

Notice it doesn’t matter if we define \([x]\) to be \(\{a \in X: x \sim a\}\), because an equivalence relation is symmetric: \(x \sim a\) if and only if \(a \sim x\).

Let’s work out some equivalence classes for the congruence modulo 2 relation on \(\mathbb{Z}\). Recall that \(x\) and \(y\) are congruent modulo 2 if and only if \(x-y\) is divisible by 2 (that is, \(x-y\) is even).

The equivalence class of \(0\), which we write as \([0]\) is the set of all integers \(y\) such that \(y\) is congruent to 0 modulo 2, in other words, all integers \(y\) such that \(y-0\) is even. So it’s the set of all even integers. \[ [0] = \{ \ldots, -4, -2, 0, 2, 4, \ldots \}\]

Now let’s do \([4]\). This is the set of all integers \(y\) such that \(y\) is congruent to 4 modulo 2, that is, all integers \(y\) such that \(y-4\) is even. Again, \(y-4\) is even if and only if \(y\) is even, so \([4]\) is the set of all even integers

\[ [4] = \{\ldots, -4, -2, 0, 2, 4 ,\ldots, \} = [0] \]

(So the equivalence classes of two different things can be equal).

Now let’s work out the equivalence class \([1]\). An integer \(y\) is congruent to 1 modulo 2 if and only if \(y-1\) is even. That’s true if and only if \(y\) is odd, so \([1]\) is the set of all odd numbers:

\[ [1] = \{ \ldots, -3, -1, 1, 3, \ldots \} \]

What about \([-3]\)? An integer \(y\) is congruent to \(-3\) modulo 2 if and only if \(y- (-3)\) is even. This is again true if and only if \(y\) is odd, so

\[[-3] = \{\ldots, -3, -1, 1, 3, \ldots \} = [1].\]

There are exactly two different equivalence classes, one being the set of all even numbers and the other being the set of all odd numbers. Every integer belongs to exactly one of these equivalence classes. In the next video we’re going to generalise this to all equivalence relations.

Before that, you should investigate the equivalence classes for congruence modulo 3. List the elements of \([0]\), \([1]\), and \([2]\) for this relation. How do the classes relate to remainders on dividing by 3? Is \([4]\) equal to one of \([0], [1], [2]\)? What about \([-5]\)?

You will find that there are exactly three different equivalence classes this time: every class is equal to one of \([0]\), \([1]\), or \([2]\).

13 Equivalence relations and partitions

Definition of a partition of a set

A partition of a set \(X\) is a set of nonempty subsets of \(X\) called parts, such that every element of \(X\) is a member of exactly one part.

A simple example is that the set \(O\) of odd numbers and the set \(E\) of even numbers make up a partition of \(\mathbb{Z}\). Every integer is either odd or even, but not both, so every integer lies in exactly one of of the two parts \(O\) and \(E\).

Two sets \(A\), \(B\) are called disjoint if \(A \cap B = \emptyset\).

Another way to state the definition of a partition of \(X\) is to say that the union of the parts is \(X\) and that any two parts in the partition are disjoint.

Here is another example partition. Every real number is either

• strictly positive,
• strictly negative,
• or zero,

but it can’t be more than one of those things at once. So if \(P\) is the set of strictly positive numbers and \(N\) is the set of strictly negative real numbers, the sets \(P, N, \{0\}\) form a partition of \(\mathbb{R}\).

Partitions and equivalence relations

Our aim in the rest of this video is to show every partition gives rise to an equivalence relation, and every equivalence relation (on a non-empty set) gives rise to a partition.

Making an equivalence relation out of a partition

Given a partition of a set \(X\), consider the relation given by saying \(x \sim y\) if and only if \(x\) and \(y\) are elements of the same part. This is an equivalence relation:

• (R): \(x \sim x\) for all \(x\): every element is a member of the same part as itself.
• (S): \(x \sim y\) if and only if \(y \sim x\): if \(x\) and \(y\) are in the same part then \(y\) and \(x\) are in the same part.
• (T): if \(x\) and \(y\) are in the same part, and \(y\) and \(z\) are in the same part, then the part containing \(x\) and the part containing \(z\) have an element, \(y\), in common. They are therefore equal, so \(x \sim z\).

Here’s a picture of this way of constructing an equivalence relation.

The set \(X = \{1,2,3,4,5,6\}\) is shown with the partition \(\{1,2,3\}\), \(\{4,5\}\), \(\{6\}\). The equivalence relation you get from this partition is shown in the table:

\(\sim\)	1	2	3	4	5	6
1	y	y	y	n	n	n
2	y	y	y	n	n	n
3	y	y	y	n	n	n
4	n	n	n	y	y	n
5	n	n	n	y	y	n
6	n	n	n	n	n	y

In row \(i\) and column \(j\) of the table there is a y if \(i \sim j\), otherwise there is an n.

For another example the partition \(O\), \(E\) of \(\mathbb{Z}\) we saw earlier gives rise to an equivalence relation in this way, and in fact it’s the relation of congruence modulo 2.

Making a partition out of an equivalence relation

Theorem. Let \(\sim\) be an equivalence relation on a nonempty set \(X\). Then the equivalence classes under \(\sim\) are a partition of \(X\).

To prove this, we must show

1. that every equivalence class is non-empty,
2. that every element of \(X\) is an element an equivalence class, and
3. that every element of \(X\) lies in exactly one equivalence class.

Proof: Part 1 is easy. An equivalence class \([x]\) contains \(x\) as \(x \sim x\) (by property (R)), so certainly \([x] \neq \emptyset\).

This also shows that part 2 is true: every \(x \in X\) is in the equivalence class \([x]\), so every element of \(X\) is an element of at least one equivalence class.

Finally let’s do part 3. How could it fail to be true that every element was in exactly one equivalence class? There would have to be an element of \(X\) in (at least) two different equivalence classes. To show that can’t happen, we’ll show that if \(x \in X\) lies in two classes \([y]\) and \([z]\), it must be that \([y] = [z]\).

Suppose \(x \in [y] \cap [z]\). Let’s show \([y] \subseteq [z]\) first. To do that, we take any \(a \in [y]\) and show \(a \in [z]\).

First, \(a\sim y\), and \(x \in [y]\) so \(x\sim y\). By (S), \(y\sim x\), so by (T) \(a\sim x\). Now \(x \in [z]\), so \(x\sim z\), so by (T) again \(a\sim z\), so \(a \in [z]\). We have \([y] \subseteq [z]\).

By the same argument, \([z]\subseteq [y]\), so \([z] = [y]\). The proof is finished.

Here’s a picture of this argument. The double-arrows illustrate that \(x\sim y\) and \(y\sim x\), and \(x \sim z\) and \(z \sim x\). The arrows between \(a\) and \(y\) illustrate that \(y \sim a\) and \(a \sim y\), and the dotted arrow shows us using property (T) to deduce that \(a \sim x\).

14 Introduction to permutations

Definition of a permutation

• A permutation of a set \(X\) is a bijection \(X \to X\).
• \(S_n\), the symmetric group on n letters, is the set of all permutations of \(\{1,2,\ldots, n\}\).

The name “group” is a foreshadowing - we will meet groups later.

Here are some examples.

• for any set \(X\), the identity function \(\operatorname{id}_X: X \to X\) is a permutation.
• The function \(f: \{1, 2, 3\} \to \{1, 2, 3\}\) given by \(f(1)=3, f(2)=2, f(3)=1\) is a permutation. \(f\) is an element of \(S_3\).
• The function \(g : \{1,2,3,4\} \to \{1, 2, 3, 4\}\) give by \(g(1)=2, g(2)=3, g(3)=4, g(4)=1\) is a permutation. \(g\) is an element of \(S_4\).

Here are some diagrams illustrating the permutations \(f\) and \(g\):

Two-row notation

We need a way of writing down elements of \(S_n\). The simplest is called two row notation. To represent \(f \in S_n\), you write two rows of numbers. The top row is 1, 2, …, n. Then underneath each number \(i\) on the top row you write \(f(i)\):

\[\begin{pmatrix} 1 & 2 & \cdots & n \\ f(1) & f(2) & \cdots & f(n) \end{pmatrix}\]

As an example, here are the two row notations for the two permutations of the previous example

\[\begin{align*} f &: \begin{pmatrix} 1&2&3\\3&2&1 \end{pmatrix} \\ g &: \begin{pmatrix} 1&2&3&4\\ 2&3&4&1 \end{pmatrix} \end{align*}\]

The two row notation for the identity in \(S_n\) is particularly simple: \[ \begin{pmatrix} 1 & 2 & \cdots & n-1 & n \\ 1 & 2 & \cdots & n-1 & n \end{pmatrix}. \]

This is a simple and not that efficient notation (it is not feasible to write down an element of \(S_{100}\) this way, even if it is a very simple permutation e.g. swaps 1 and 2, leaves 3-100 alone), but it is at least concrete and simple.

How many permutations?

Theorem. \(|S_n| = n!\)

(\(n!\) means \(n\times (n-1) \times \cdots \times 2 \times 1\))

Proof: Instead of counting permutations we will count possible bottom rows of two row notations for elements of \(S_n\). Because a permutation is a bijection - one-to-one and onto - this bottom row consists of the numbers 1, 2, …, n in some order. We just need to show that there are exactly \(n!\) different ways to order the numbers 1, 2, … , n.

We prove this by induction on \(n\). For the base case \(n=1\) we have \(1!=1\) and it is clear that there is only one way to order a single 1.

For the inductive step, suppose \(|S_{n-1}| = (n-1)!\). An ordering of 1, 2, …, n arises in exactly one way as an ordering of 1, 2, …, (n-1) with the number n inserted into one of n places (the first, or second, or …, or nth position). So the number of such orderings is \(|S_{n-1}|\) (the number of ways to choose an ordering of 1, 2, …, (n-1)) times the number of ways to insert an n, giving \(|S_n| = |S_{n-1}| \times n = (n-1)!\times n = n!\). This completes the inductive step.

For example, there are \(2! = 2\) elements of \(S_2\): they are

\[\begin{pmatrix} 1&2\\1&2 \end{pmatrix}, \begin{pmatrix} 1&2\\2&1 \end{pmatrix}\]

(The first one is the identity function on \(\{1,2\}\)).

Permutations turn out to be very important for the rest of the course, especially \(S_n\), so we will spend some time on them and their properties.

15 Inverses and composition

Inverse of a permutation

Permutations are bijections, so they have inverse functions. The inverse function to a permutation \(\sigma\) undoes what \(\sigma\) did, in the sense that if \(\sigma(x) = y\) then \(\sigma^{-1}(y) = x\)

In two row notation you write \(\sigma(x)\) beneath \(x\). So you can get the two row notation for \(\sigma^{-1}\) by swapping the rows (and reordering)

Example:

\[\begin{align*}\sigma & = \begin{pmatrix}1&2&3&4\\2&3&4&1\end{pmatrix} \\ \sigma^{-1} &= \begin{pmatrix}2&3&4&1\\1&2&3&4\end{pmatrix} = \begin{pmatrix}1&2&3&4\\4&1&2&3\end{pmatrix}\end{align*}\]

Composition of permutations

We know that the composition of two bijections is a bijection. So the composition of two permutations of a set \(X\) is again a permutation of \(X\).

For example, let

\[\begin{align*} \sigma &= \begin{pmatrix}1&2&3\\2&1&3\end{pmatrix} \\ \tau & = \begin{pmatrix}1&2&3\\1&3&2\end{pmatrix} \end{align*}\]

Then \(\sigma\circ\tau\) is the function \(\{1,2,3\}\to \{1,2,3\}\) whose rule is “do \(\tau\), then do \(\sigma\).” Thus

\[\begin{align*} (\sigma\circ\tau)(1) &= \sigma(\tau(1)) = \sigma(1) = 2 \\ (\sigma\circ\tau)(2) &= \sigma(\tau(2)) = \sigma(3) = 3 \\ (\sigma\circ\tau)(3) &= \sigma(\tau(3)) = \sigma(2) = 1 \end{align*}\]

In two row notation,

\[\sigma \circ \tau = \begin{pmatrix} 1&2&3\\ 2 & 3 & 1 \end{pmatrix}\]

Composition isn’t commutative

This composition has an interesting property: the order matters.

With \(\sigma\) and \(\tau\) as before, \(\begin{align*} \sigma\circ\tau &= \begin{pmatrix} 1&2&3\\ 2&3&1 \end{pmatrix} \\ \tau\circ\sigma &= \begin{pmatrix} 1&2&3\\ 3&1&2 \end{pmatrix} \end{align*}\)

They’re different: composition of permutations is not commutative in general.

Definition: Two permutations \(s\), \(t\) are said to commute if \(s\circ t=t\circ s\).

16 Cycles

Cycle definition and notation

We’re going to introduce a more efficient way of writing permutations. This involves thinking about a special kind of permutation, called a cycle.

Let \(m>0\), let \(a_0,\ldots, a_{m-1}\) be distinct positive integers. Then \[(a_0,\ldots,a_{m-1})\] is defined to be the permutation such that

• \(a_i\) goes to \(a_{i+1}\) for \(i<m-1\), \(a_{m-1}\) goes to \(a_0\), and
• any number which isn’t an \(a_i\) goes to itself.

If we write \(a_m := a_0\) then we could just say \(a_i \mapsto a_{i+1}\) then we could just say \(a_i \mapsto a_{i+1}\) for all \(i\).

Definition: A permutation of the form \((a_0, \ldots, a_{m-1})\) is called an \(m\)-cycle. A permutation which is an \(m\)-cycle for some \(m\) is called a cycle.

Two important things to note:

• any 1-cycle is equal to the identity permutation
• if we just write down the cycle \((1,2,3)\), say, it could be could be an element of \(S_3\), or \(S_4\), or \(S_5\), or any other \(S_n\) with \(n\geq 3\). When it matters, we will make this clear.

Example:

• In \(S_3\), the 2-cycle \((1, 2)\) is the permutation that sends 1 to 2, 2 to 1, and 3 to 3. In two row notation \((1,2)= \begin{pmatrix} 1&2&3\\2&1&3 \end{pmatrix}\).
• In \(S_4\), the 3-cycle \((2, 3, 4)\) is the permutation that sends 1 to 1, 2 to 3, 3 to 4, and 4 to 2. In two row notation \((2,3,4) = \begin{pmatrix} 1&2&3&4\\1&3&4&2 \end{pmatrix}\).

The picture below is of the 5-cycle \((1,2,3,4,5)\), illustrating why these permutations are called “cycles”.

Multiple ways to write the same cycle

Consider the two cycles \(a = (1, 2, 3, 4)\) and \(b = (2,3,4,1)\).

\(a\) sends 1 to 2, 2 to 3, 3 to 4, 4 to 1, and any other number to itself. So does \(b\). So \(a=b\).

Similarly if \(c = (3, 4, 1, 2)\) and \(d=(4,1,2,3)\) then \(a=b=c=d\).

Contrast this with two row notation, where there was only one way to write a given permutation.

In general, every \(m\)-cycle can be written \(m\) different ways since you can put any one of the \(m\) things in the cycle first.

Another example: in \(S_5\), \[(5,3, 2) = (3, 2, 5) = (2, 5, 3).\]

Disjoint cycles

Two cycles \((a_0,\ldots,a_{m-1})\) and \((b_0,\ldots, b_{k-1})\) are disjoint if no \(a_i\) equals any \(b_j\).

Example:

• (1,2,7) is disjoint from (5,4)
• (1,2,3) and (3,5) are not disjoint.

One reason disjoint cycles are important is that disjoint cycles commute. If \(a\) and \(b\) are disjoint cycles, \(a\circ b = b \circ a\). This is a special property, as you have seen that in general for two permutations \(s\) and \(t\), \(s\circ t \neq t \circ s\).

Inverse of a cycle

For every permutation \(s\) there is an inverse permutation \(s^{-1}\) such that \(s \circ s^{-1} = s^{-1} \circ s = \operatorname{id}\).

How do we find the inverse of a cycle? \(a = (a_0, \ldots, a_{m-1})\) sends \(a_i\) to \(a_{i+1}\) for all \(i\) (and every number not equal to an \(a_i\) to itself), so \(a^{-1}\) should send \(a_{i+1}\) to \(a_i\) for all \(i\) (and every number not equal to an \(a_i\) to itself).

In other words, \(a^{-1}\) is the cycle \((a_{m-1}, a_{m-2}, \ldots, a_1, a_0)\):

\[(a_0, \ldots, a_{m-1}) ^{-1} = (a_{m-1}, a_{m-2}, \ldots, a_1, a_0) \]

As a special case, the inverse of the 2-cycle \((i, j)\) is \((j, i)\). But \((i, j) = (j,i)\)! So every 2-cycle is its own inverse.

If we draw cycles as we did before, their inverses are obtained by “reversing the arrows.”

Not all permutations are cycles

Not every permutation is a cycle.

Example: \(\sigma = \begin{pmatrix}1&2&3&4\\2&1&4&3\end{pmatrix}\). This is not a cycle. Suppose it was. \(\sigma\) sends 1 to 2, and 2 to 1, so if it were a cycle it would have to be \((1,2)\). But \((1,2)\) sends 3 to 3, whereas \(\sigma(3)=4\), so \(\sigma \neq (1,2)\).

Here is a diagram of the permutation \(\sigma\):

While \(\sigma\) is not a cycle, it is the composition of two cycles: \(\sigma = (1, 2)\circ (3,4)\). In fact, every permutation can be written this way.

17 Products of disjoint cycles

Every permutation is a product of disjoint cycles

Here is our previous example: \(\sigma = \begin{pmatrix} 1&2&3&4\\2&1&4&3 \end{pmatrix}\). This isn’t a cycle, but it does equal \((1,2) \circ (3,4)\).

This is suggestive of the following theorem.

Theorem: Every \(s \in S_n\) equals a product of disjoint cycles.

Proof. Define a relation on \(\{1, 2, \ldots, n\}\) by \(x \sim y\) if and only if there exists an integer \(r\) such that \(y = s^r(x)\). This is an equivalence relation.

Note that for every \(x \in \{1,2,\ldots, n\}\), there is a positive number \(l\) such that \(s^l(x) = x\). For the elements \[ x, s(x), s^2(x), \ldots \] cannot all be different as there are only \(n\) possible values, namely 1, 2, …, \(n\), for \(s^r(x)\). So for some \(i<j\) we have \(s^i(x) = s^j(x)\). Applying the function \(s^{-i}\) to both sides of this equation, \(x = s^{j-i}(x)\).

It follows that there is a smallest positive number \(l\) such that \(s^l(x) = x\).

I claim that the equivalence class \([x]\) equals \(\{x, s(x), s^2(x), \ldots, s^{l-1}(x)\}\) where \(l\) is this smallest positive number such that \(s^l(x) = x\). It is immediate from the definition of \(\sim\) that \[ \{x, s(x), \ldots, s^{l-1}(x) \} \subseteq [x] \] so we just need to show that \([x] \subseteq \{x, s(x), \ldots, s^{l-1}(x)\}\). Let \(y \in [x]\). Certainly \(y = s^r(x)\) for some \(r \in \mathbb{Z}\), but we must show \(y\) is equal to a power of \(s\) between 0 and \(l-1\) applied to \(x\). Divide \(r\) by \(l\), getting quotient \(q\) and remainder \(t\), so \(r = ql + t\) where \(0 \leq t < l\). Since \(s^l(x)=x\), we have \(s^{ql}(x) = x\) too. So \[y = s^r(x) = s^{t+ql}(x) = s^t(s^{ql}(x)) = s^t(x)\] by the exponent laws. It follows \(y \in \{x, s(x), \ldots, s^{l-1}(x)\}\), proving the claim.

I also claim that all the numbers \(x, s(x), s^2(x), \ldots, s^{l-1}(x)\), with \(l\) as defined above, are different. If two of them were equal, then there would be numbers \(i\) and \(j\) with \(0 \leq i < j < l\) such that \(s^i(x) = s^j(x)\). Then applying the function \(s^{-i}\) to both sides of this equation and using the exponent laws, \(x = s^{j-i}(x)\). But \(0 < j-i < l\). This would contradict \(l\) being the smallest positive number such that \(s^l(x) = x\).

This means that the cycle \(c_x = (x, s(x), \ldots, s^{l-1}(x))\) makes sense (remember, part of the definition of a cycle \((a_0, \ldots, a_{m-1})\) was that all the \(a_i\) should be different). Furthermore, \(c_x(i) = s(i)\) for each \(i\) in the equivalence class of \([x]\), because we know that equivalence class is just \(x, s(x), \ldots, s^{l-1}(x)\). (**)

Now let the distinct equivalence classes be \([x_1], [x_2], \ldots, [x_m]\). Notice that the cycles \(c_{x_1}, c_{x_2}, \ldots, c_{x_m}\) are disjoint, because the entries in the cycle \(c_{x_j}\) are the elements of the equivalence class of \(x_j\), and any two distinct equivalence classes are disjoint.

I claim that \[ s = c_{x_1} \circ c_{x_2} \cdots c_{x_m}. \] Since the right hand side is a product of disjoint cycles, this will finish the proof. This is a claim that two functions \(\{1, 2, \ldots, n\} \to \{1, 2, \ldots, n\}\) are equal, so to check it we need to show that for each \(1 \leq i \leq n\) we have \[ s(i) = (c_{x_1} \circ c_{x_2} \cdots c_{x_m})(i). \]

Fix such a number \(i\). Remember that the equivalence classes are a partition of \(\{1,2,\ldots, n\}\), so \(i\) belongs to exactly one of the equivalence classes \([x_1], \ldots, [x]_m\). Say \(i \in [x_j]\), so that \(i \notin [x_k]\) for any \(k \neq j\). Then

• For each \(k \neq j\), \(c_{x_k}\) sends \(i\) to \(i\). For \(c_{x_k}\) sends everything not in \([x_k]\) to itself, and \(x \notin [x_k]\)
• For each \(k \neq j\), \(c_{x_k}\) sends \(s(i)\) to \(s(i)\). This is because \(s(i) \in [x_j]\) too, so the same argument applies.
• We already established, at (**), that \(c_{x_j}(i) = s(i)\).

It follows that \((c_{x_1} \circ c_{x_2} \cdots c_{x_m})(i) = s(i)\), and we’re done.

To understand the proof, it helps to follow it through with a particular example in mind. Say \[s = \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 7&3&2&1&5&9&4&6&8 \end{pmatrix}\]

The equivalence classes are \([1] = \{1,7,4\}, [2] = \{2,3\}, [5] = \{5\}, [6] = \{6,8,9\}\). So the \(x_i\)s in the proof could be 1, 2, 5, 6. (Or they could be 7, 3, 5, 9, or many other possibilities - we just have to take one element from each equivalence class).

The smallest positive power of \(s\) sending 1 to itself is \(s^3\), the smallest positive power of \(s\) sending \(2\) to itself is \(s^2\), the smallest positive power of \(s\) sending 5 to itself is \(s^1\), and the smallest positive power of \(s\) sending 6 to itself is \(s^3\) - these are the numbers \(l\) in the proof.

The cycles arising from these equivalence classes are

\[\begin{align*} (1, s(1), s^2(1)) &= (1, 7, 4) \\ (2, s(2)) &= (2, 3) \\ (5) &= (5) \\ (6, s(6), s^2(6)) &= (6,9, 8) \end{align*}\]

The outcome of the proof is that \[s = (1,7,4)(2,3)(5)(6,9,8).\]

Non-uniqueness

There can be many different ways to write a given permutation as a product of disjoint cycles. For example, taking the permutation \(s\) we’ve just seen,

\[\begin{align*}s &= (1,7,4)(2,3)(5)(6,9,8)\\ &= (7,4,1)(2,3)(6,9,8) \\ &= (2,3)(6,9,8)(7,4,1) \\ &= \ldots \end{align*}\]

The two things you should remember are that an \(m\)-cycle can be written in \(m\) different ways - \((1,2,3)=(2,3,1)=(3,1,2)\) - and that disjoint cycles commute - \((1,2)(3,4) = (3,4)(1,2)\).

How to find a disjoint cycle decomposition

A disjoint cycle decomposition of a permutation \(\sigma\) is a product of disjoint cycles which equals \(\sigma\). For example

\[\begin{pmatrix} 1&2&3&4\\ 2&1&4&3 \end{pmatrix} = (1,2)(3,4)\]

is a disjoint cycle decomposition for the permutation discussed at the start of this video.

The theorem we just saw tells us every permutation has a disjoint cycle decomposition. It also gives a method of finding a disjoint cycle decomposition for a permutation given in 2-row notation, or in some other format that isn’t a disjoint cycle decomposition:

To find a disjoint cycle decomposition for \(\sigma \in S_n\):

1. pick a number that doesn’t yet appear in a cycle
2. compute its image, and the image of that, and so on, until you have a cycle. Write down that cycle.
3. if all elements of 1..n are in one of your cycles, stop, else go to 1.

Example: Let \(s = \begin{pmatrix} 1&2&3&4&5&6&7 \\ 7&6&3&1&2&5&4 \end{pmatrix}\). We pick a number not yet in a cycle, say 1. 1 goes to 7, 7 goes to 4, 4 goes to 1. We are back to the number we started with, so our first cycle is \((1,7,4)\). Now we pick another number not in a cycle, say 2. \(s\) sends 2 to 6, 6 to 5, and 5 to 2. That’s another cycle, so we have \((1,7,4)(2,6,5)\). Now we pick another number not yet in a cycle - the only one left is 3. \(s\) sends 3 to 3, so this is immediately a cycle. We have \(s = (1,7,4)(2,6,5)(3)\).

As we saw when we defined cycles, any 1-cycle is equal to the identity function. For that reason (and because 1-cycles look confusingly like what we write when we evaluate a function) we usually omit 1-cycles like \((3)\) from disjoint cycle decompositions, so we’d write \(s = (1,7,4)(2,6,5)\).

Composing permutations given as products of disjoint cycles

Let’s work out a disjoint cycle decomposition for \(\sigma\tau\) where

\[\begin{align*} \sigma &= (4,2,6,1,5) \\ \tau &= (5,4,7,3,8) \end{align*}\]

are elements of \(S_8\).

Remember that \(\sigma\tau\) means do \(\tau\), then do \(\sigma\). Keeping that in mind, all we have to do is follow the instructions from before. Start with 1:

\[\begin{align*} \sigma(\tau(1)) &= \sigma(1) = 5\\ \sigma(\tau(5)) &= \sigma(4) = 2 \\ \sigma(\tau(2)) &= \sigma(2) = 6\\ \sigma(\tau(6)) &= \sigma(6) = 1 \end{align*}\]

…and we have our first cycle, \((1, 5, 2, 6)\). Continuing with a number not yet in a cycle, say 3, we get

\[\begin{align*} \sigma(\tau(3)) &= \sigma(8) = 8\\ \sigma(\tau(8)) &= \sigma(5) = 4 \\ \sigma(\tau(4)) &= \sigma(7) = 7\\ \sigma(\tau(7)) &= \sigma(3) = 3 \end{align*}\]

…and we have our next cycle, \((3,8,4,7)\). There are no numbers left, so

\[\sigma\tau = (1,5,2,6)(3,8,4,7).\]

You should do \(\tau\sigma\) now. You’ll find that your disjoint cycle decomposition has two 4-cycles again.

For another example, let’s find a disjoint cycle decomposition for \((1,2)(2,3)(3,4)\). Write \(a = (1,2), b = (2,3), c = (3,4)\).

Again, remember that this composition means “do \(c\), then do \(b\), then do \(c\).” So starting with 1 as usual,

\[\begin{align*} a(b(c(1))) &= a(b(1)) = a(1) = 2 \\ a(b(c(2))) &= a(b(2)) = a(3) = 3 \\ a(b(c(3))) &= a(b(4)) = a(4) = 4 \\ a(b(c(4))) &= a(b(3)) = a(2) = 1 \end{align*}\]

and so \(abc = (1,2,3,4)\).

18 Powers and orders

Powers of a permutation

Since the composition of two permutations is another permutation, we can form powers of a permutation by composing it with itself some number of times.

Definition: Let \(s\) be a permutation and let \(m\) be an integer. Then \[s^m = \begin{cases} s\cdots s \; (m \text{ times}) & m>0 \\ \operatorname{id} & m = 0 \\ s^{-1}\cdots s^{-1} \; (-m \text{ times}) & m<0 \end{cases}\]

It’s tedious but straightforward to check that for any integers \(a\), \(b\),

• \(s^a\circ s^b = s^{a+b}\), and
• \((s^a)^b = s^{ab}\)

so that some of the usual exponent laws for real numbers hold for composing permutations. The two facts above are called the exponent laws for permutations.

We very often emphasise this analogy between multiplying numbers and composing permutations by talking about “multiplying” two permutations when we mean composing them, calling their composition their “product”, and writing it as \(st\) instead of \(s \circ t\).

But be careful: there are some differences. As we’ve seen, permutation composition is not commutative unlike real number multiplication, and as we saw earlier, \((s\circ t)^{-1} = t^{-1}\circ s^{-1}\)

Order of a permutation

Definition: The order of a permutation \(\sigma\), written \(o(\sigma)\), is the smallest strictly positive number \(n\) such that \(\sigma^n = \operatorname{id}\).

For example, let

\[\begin{align*} s &= \begin{pmatrix} 1&2&3\\ 2&3&1 \end{pmatrix} \\ t &= \begin{pmatrix} 1&2&3\\ 2&1&3 \end{pmatrix}\end{align*}\]

You should check that \(s^2 \neq \operatorname{id}\) but \(s^3 = \operatorname{id}\), so the order of \(s\) is 3, and that \(t \neq \operatorname{id}\) but \(t^2 = \operatorname{id}\) so the order of \(t\) is 2.

Order of an \(m\)-cycle

Lemma: the order of an \(m\)-cycle is \(m\).

Proof: ⬛⬛⬛⬛⬛ ⬛⬛⬛ ⬛⬛⬛⬛ ⬛ ⬛⬛ ⬛⬛⬛⬛⬛ ⬛⬛⬛⬛⬛⬛ ⬛⬛⬛⬛⬛⬛⬛

19 Transpositions

Definition of a transposition

A transposition is a 2-cycle.

For example, the only transpositions in \(S_3\) are \((1,2)\), \((2,3)\), and \((1,3)\).

Every permutation is a product of transpositions

One way we’ve already seen of illustrating a permutation \(s\) in \(S_n\) is to draw the numbers 1, 2, …, n in a column, and then in another column to its right, and draw a line from each number \(i\) in the first column to \(s(i)\) in the second. You get what looks like a lot of pieces of string tangled together.

Here is a diagram of the permutation \(s= (1,2,3,4,5)\). Think of the lines as pieces of string connecting \(i\) on the left with \(s(i)\) on the right.

Composing two permutations drawn in this way corresponds to placing their diagrams side-by-side:

Imagine taking such a diagram and stretching it out. You could divide it up into smaller diagrams, each of which contains only one crossing of strings.

A diagram with a single string crossing is a transposition, since only two numbers change place. The diagram above illustrates the fact that \[ (1,2,3,4) = (1,2)(2,3)(3,4).\]

But this would work for any permutation, which suggests…

Theorem: every permutation equals a product of transpositions.

To prove this, we’ll need a lemma.

Lemma: every cycle equals a product of transpositions

Proof of the lemma: we show by induction on \(m\) that

\[(a_0,\ldots,a_{m-1}) = (a_0,a_1)(a_1,a_2)\ldots (a_{m-2},a_{m-1}).\]

This is obvious for \(m=1\). Now suppose \(m>1\). Then

\[(a_0,a_1)\cdots(a_{m-3}, a_{m-2})(a_{m-2}, a_{m-1}) = (a_0, a_1, \ldots, a_{m-2})(a_{m-2}, a_{m-1})\]

by the inductive hypothesis. We must show this equals \((a_0, \ldots, a_{m-1})\). Let \(c = (a_0, \ldots, a_{m-1})\), \(t = (a_0, \ldots, a_{m-2})\), \(u = (a_{m-2}, a_{m-1})\) so that we are claiming \(c=tu\). To prove that the two functions \(c\) and \(tu\) are equal, we have to prove that \(c(x) = t(u(x))\) for all \(x\). We can do this case by case:

• if \(x \neq a_i\) for any \(i\) then \(c(x)=x\), \(u(x)=x\), and \(t(x)=x\), so \(c(x) = t(u(x))\).
• if \(x=a_i\) for some \(0 \leq i < m-1\) then \(c(x)=a_{i+1}\), \(u(x) = a_i\), and \(t(a_i)=a_{i+1}\), so \(c(x) =a_{i+1} = t(u(x))\).
• if \(x=a_{m-2}\) then \(c(x) = a_{m-1}\), \(u(x) = a_{m-1}\), and \(t(a_{m-1})=a_{m-1}\), so \(c(x) = a_{m-1} = t(u(x))\).
• finally, if \(x=a_{m-1}\) then \(c(x) = a_0\), \(u(x) = a_{m-2}\), and \(t(a_{m-2}) = a_0\), so \(c(x) = a_0 = t(u(x))\).

In every case \(c\) and \(tu\) agree, so \(c=tu\), proving the lemma.

Proof of the theorem: let \(p\) be a permutation. We have seen that every permutation can be written as a product of cycles, so there are cycles \(c_1,\ldots, c_k\) such that \(p=c_1\cdots c_k\). The lemma above shows how to write each \(c_i\) as a product of transpositions, which expresses \(p\) as a product of transpositions too.

Example. Suppose we want to express

\[s = \begin{pmatrix} 1&2&3&4&5&6\\ 2&3&1&5&6&4 \end{pmatrix}\]

as a product of transpositions. A disjoint cycle decomposition for \(s\) is

\[ s = (1,2,3)(4,5,6)\]

and applying the lemma above, we get

\[\begin{align*} (1,2,3) &= (1,2)(2,3)\\ (4,5,6) &= (4,5)(5,6) \end{align*}\]

So

\[s = (1,2,3)(4,5,6) = (1,2)(2,3)(4,5)(5,6).\]

Adjacent transpositions

An adjacent transposition is one of the form \((i, i+1)\).

This name is used because an adjacent transposition swaps two adjacent numbers, \(i\) and \(i+1\).

The only adjacent transpositions in \(S_5\) are \((1,2)\), \((2,3)\), \((3,4)\), and \((4,5)\).

20 Sign of a permutation

Definition of odd and even permutations

Now we know that every permutation can be expressed as a product of transpositions, we can make the following definition.

• A permutation is odd if it can be expressed as a product of an odd number of transpositions and even if it can be expressed as an even number of transpositions.
• The parity of a permutation is whether it is odd or even.

Examples:

• \((a,b)\) is odd.
• \(\operatorname{id} = (1,2)(1,2)\) is even.
• \((1,2,3) = (1,2)(2,3)\) is even.
• \((a_0,\ldots,a_{m-1})\) is even if \(m\) is odd and odd if \(m\) is even.

Odd or even theorem

It seems possible that a permutation could be odd AND even at the same time, but this isn’t the case.

Theorem: Every permutation is odd or even but not both.

Proof: Here is an outline of how to prove this. You won’t be asked about this proof in a closed-book exam. We know that every permutation can be written as a product of transpositions, so the only problem is to prove that it is not possible to find two expressions for a fixed permutation \(p \in S_n\), one using a product \(s_1 s_2 \cdots s_{2m+1}\) of an odd number of transpositions and one using a product \(t_1 t_2 \cdots t_{2l}\) of an even number of transpositions. The steps are as follows:

• If this were the case then we would have \(\operatorname{id} = t_{2l}\cdots t_1 s_1 \cdots s_{2m+1}\), expressing the identity as a product of an odd number of transpositions, so it is enough to prove that this is impossible.
• Observe that any transposition \((i,j)\) can be written as a product of an odd number of adjacent transpositions, as follows. Without loss of generality (as \((i,j)=(j,i)\)) assume \(i<j\). Let \(a =(j-1,j)\cdots (i+2,i+3)(i+1,i+2)\). Then \((i,j) = a (i, i+1) a^{-1}\).
• So it is enough to show that the identity cannot be written as a product of an odd number of adjacent transpositions. Assume, for a contradiction, that it can be so written.
• Consider polynomials in the \(n\) variables \(x_1,\ldots,x_n\). If you have such a polynomial \(f(x_1,\ldots,x_n)\) and a permutation \(\sigma \in S_n\), you get a new polynomial \(\sigma(f)\) by replacing each \(x_i\) in \(f\) with \(x_{\sigma(i)}\). For example, if \(\sigma = (1,2,3)\) and \(f=x_1+x_2^2\) then \(\sigma(f)=x_2+x_3^2\)
• Define \(\Delta = \prod_{1\leq i<j \leq n}(x_i-x_j)\)
• Observe that for any \(k\), \((k,k+1)(\Delta) = -\Delta\), and so any product of an odd number of adjacent transpositions sends \(\Delta\) to \(-\Delta\) too.
• Get a contradiction from the fact that \(\operatorname{id}(\Delta) = \Delta\).

Sign of a permutation

• The sign of a permutation is \(1\) if it is even and \(-1\) if it is odd.
• \(\operatorname{sign}(s)\) is the sign of the permutation \(s\)

So if \(s\) can be written as a product of \(m\) transpositions, \(\operatorname{sign}(s) = (-1)^m\).

Lemma: For any two permutations \(s\) and \(t\), \(\operatorname{sign}(st) = \operatorname{sign}(s)\operatorname{sign}(t)\)

Proof: If \(s\) can be written as a product of \(m\) transpositions and \(t\) can be written as a product of \(n\) transpositions, then \(st\) can be written as a product of \(m+n\) transpositions. So

\[\begin{align*} \operatorname{sign}(st) &= (-1)^{n+m}\\ &= (-1)^m (-1)^n \\ &= \operatorname{sign}(s) \operatorname{sign}(t) \end{align*}\]

This rule about the sign of a product means that

• an even permutation times an even permutation is even,
• an even permutation times an odd permutation is odd,
• an odd permutation times an odd permutation is even

…just like multiplying integers.

Two results on the sign of a permutation

Lemma:

1. Even length cycles are odd, odd length cycles are even.
2. If \(s\) is any permutation, \(\operatorname{sign}(s) = \operatorname{sign}(s^{-1})\).

Proof:

1. we saw in the last section that if \(a = (a_0,\ldots, a_{m-1})\) is any \(m\)-cycle, \[(a_0 \ldots, a_{m-1}) = (a_0, a_1)\cdots (a_{m-2}, a_{m-1}).\] So an \(m\)-cycle is a product of \(m-1\) transpositions. Therefore
   • if \(m\) is even \(a\) is a product of the odd number \(m-1\) of transpositions, so \(a\) is odd.
   • if \(m\) is odd \(a\) is a product of the even number \(m-1\) of transpositions, so \(a\) is even.
2. If \(s = t_1\cdots t_m\) is a product of \(m\) transpositions, \(s^{-1} = t_m^{-1}\cdots t_1^{-1}\). But the inverse of a transposition is a transposition, so \(s^{-1}\) is also the product of \(m\) transpositions.

It follows from the first part of the lemma that \(\operatorname{sign} (a_0, \ldots ,a_{m-1}) = (-1)^{m-1}\)

Application

Here’s one of the many reasons the sign of a permutation is useful. Take a Rubik’s cube, and swap the middle colours on two faces. Is it still solvable? No, because all Rubik’s cube moves are even permutations of the faces.