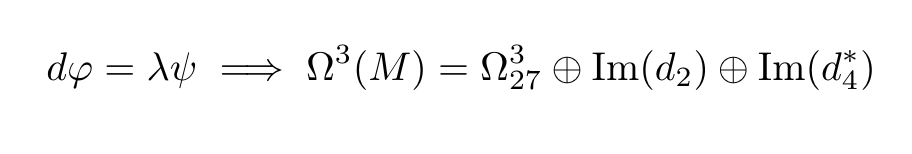KCL/UCL Junior Geometry Seminar

Thu 30.04.20

17.00-18.15

Location: Zoom

Title: Resolution of 4-dimensional symplectic orbifolds

Speaker: Lucía Martín Merchán

Abstract: An orbifold is a space which is locally modelled on balls of the euclidean space quotient by a finite group. These have been very useful in many geometrical contexts; in the setting of symplectic geometry, symplectic orbifolds have been introduced mainly as a way to construct symplectic manifolds by resolving their singularities. Some authors have provided methods for resolving particular types of symplectic orbifold singularities; but there are no techniques to resolve general symplectic orbifolds.
In this talk we give a method to resolve arbitrary symplectic 4-orbifolds making use of techniques of resolution of quotient singularities and gluing symplectic forms. This is a joint work with J. Rojo.

Thu 07.05.20

Title: No talk

Thu 14.05.20

17.00-18.15

Location: Zoom

Title: Spin(7) metrics admitting Kähler reduction

Speaker: Udhav Fowdar

Abstract: Spin(7) manifolds are Ricci flat 8-dimensional Riemannian manifolds. Together with G2, they form the class of exceptional holonomy manifolds. The first examples were constructed by Bryant and Salamon in 1989 and since then many more have appeared, though very few explicit. In this talk, I will describe a method of finding many explicit local examples of Spin(7) metrics admitting 2-torus actions such that the quotient 6-manifolds are Kähler. The key ingredients will be the symplectic reduction and the Gibbons-Hawking ansatz. The talk will be non-technical and I will give a comprehensive background.

Thu 21.05.20

17.00-18.15

Location: Zoom

Title: Deformation theory of nearly G_2 manifolds

Speaker: Ragini Singhal

Abstract: In this talk we will discuss the deformation theory of nearly G_2 manifolds. We will start by describing some identities for 2 and 3 forms on such manifolds. After introducing a Dirac type operator we will prove a result on the cohomology of nearly G_2 manifolds. Along the way we will reprove a result of Alexandrov—Semmelman on the space of infinitesimal deformation of nearly G_2 structures. Finally we will discuss the progress so far for the second order deformations. This is all a joint work with Shubham Dwivedi (University of Waterloo).

Thu 28.05.20

17.00-18.15

Location: Zoom

Title: Cohomogeneity one Spin(7)-manifolds

Speaker: Fabian Lehmann

Abstract: An 8-dimensional Riemannian manifold with holonomy group contained in Spin(7) is Ricci-flat, but not Kahler. The condition that the holonomy reduces to Spin(7) is equivalent to a complicated system of non-linear PDEs. In the non-compact setting, symmetries can be used to reduce this complexity. In the case of cohomogeneity one manifolds, i.e. where a generic orbit has codimension one, the non-linear PDE system reduces to a nonlinear ODE system. I will discuss examples where existence questions of Spin(7) holonomy metrics give rise to an interesting problem for ODE systems.

Thu 04.06.20

17.00-18.15

Location: Zoom

Title: $SU(2)^2\times U(1)$-invariant $G_2$-instantons

Speaker: Matt Turner

Abstract: $G_2$-instantons in 7-dim are analogous to ASD-instantons in 4-dim; this motivates the idea of using $G_2$-instantons to construct enumerative invariants of $G_2$-manifolds. Therefore it is natural to search for examples of $G_2$-instantons on all known constructions of $G_2$-manifolds. This becomes easier when the manifolds have a high level of symmetry. In this talk, we consider $G_2$-manifolds which have a cohomogeneity one action of $SU(2)^2\times U(1)$, while also being asymptotically conical. We will discuss the progress that has been made to find instantons on these manifolds.

Thu 11.06.20

17.00-18.15

Location: Zoom

Title: t.b.c.

Speaker: t.b.c.

Abstract:

Thu 10.10.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Cutting up surfaces and commutators in free groups

Speaker: David Sheard

Abstract: When is an element $g\in G$ of a group a product of commutators $[a,b]$? What is the minimal number of commutators $n$ such that $g=[a_1,b_1]\cdots[a_n,b_n]$? What are all possible solutions $(a_1,b_1,\dots,a_m,b_m)$ to the equation $g=[a_1,b_1]\cdots[a_m,b_m]$? Very difficult, yet important, questions --- but ones whose answers seem to lie in the darkest recesses of combinatorial group theory.

Not so! At least for $G$ a free group, these questions can all be answered elegantly and beautifully by cutting up and colouring surfaces. In this talk I shall present solutions to these problems with an emphasis on drawing nice pictures.

Thu 17.10.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Character Varieties of Surface Groups

Speaker: John McCarthy

Abstract: The points of a character variety classify the representations of a group up to equivalence. Such representation-theoretic objects admit alternative descriptions coming from symplectic geometry, algebraic geometry, and gauge theory. In this we will investigate the character varieties of surface groups, and discuss their relationship to important moduli spaces appearing in algebraic and differential geometry.

Thu 24.10.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Calibrated Submanifolds

Speaker: Benjamin Aslan

Abstract: Geodesics on a Riemannian manifold encode crucial information about its geometry such as the curvature. The same is true for the higher dimensional analogue of geodesics: minimal surfaces. On a manifold with special holonomy, there is distinguished class of minimal submanifolds, called calibrated submanifolds. The hope is that the space of calibrated submanifolds contains even finer information about the ambient manifold, potentially leading to new invariants. In this talk, we will review some basic results of calibrated geometry and then go on and see in which geometries the space of deformations of a calibrated submanifold is automatically smooth and compute its dimension.

Thu 31.10.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: J-holomorphic curves and Lagrangians

Speaker: Chris Evans

Abstract: We investigate the properties and interactions of the two most important submanifolds of symplectic spaces. The discussion will focus on geometry and intuition. We aim to cover some of the core ideas in Gromov's original paper: Gromov compactness and bubbling, existence of discs on Lagrangians, and non-standard symplectic structures.

Thu 07.11.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: An introduction to derived categories

Speaker: Bradley Doyle

Abstract: To any algebraic variety (or any ring, scheme, stack, etc) one can associate an associated category called the derived category. I will explain what this category is and provide motivation for why it is useful. After this I will cover some basic properties and results, finally I will explain one technique, semiorthogonal decompositions, that is used to study them. In the special case of projective space this will provide a connection with quiver algebras. Despite the derived category being used to study geometric objects this talk will be more algebraic than geometric.

Thu 14.11.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Handle decomposition and Kirby calculus

Speaker: Angela Wu

Abstract: Here are two interesting questions: 1. What's the best way to visualize a four dimensional manifold? 2. How can you hold a glass of wine in the palm of one hand and without changing your grip or moving your feet, rotate the glass through 720 degrees about a fixed axis without spilling the wine? The answers to both of these questions will be presented in this talk!

Thu 21.11.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: From triangles to algebraic stacks, a crash course in geometry

Speaker: Luigi Lunardon

Abstract: A stack is a category fibered in groupoids over a certain Grothendieck topology such that isomorphisms are a sheaf and every descent datum is effective.

This definition is concise and correct, but definitely not enlightening. Moreover, it doesn't motivate the necessity of introducing stacks in the study of moduli problems, nor give any geometric intuition about them.

The aim of this talk is to motivate algebraic stacks as a natural object in algebraic geometry and explain which properties we wish them to have. To do this, we start with a classifying problem for triangles, and then translate it in the language of category theory.

Thu 28.11.19

Title: Seminar Cancelled

Thu 05.12.19

Title: Seminar Cancelled

Thu 12.12.19

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Existence and regularity of area minimizers , a brief intoduction to Geometric Measure Theory

Speaker: Konstantinos Leskas

Abstract: An interesting and extensively studied mathematical problem is , given a boundary in R^n find a manifold that minimizes area with that boundary. We will start by cosidering the case of graphs and discussing existence and regularity in this setting. Then we will pass to the more general problem, see what can go wrong even in the class of graphs and motivate ourselves to work with a more general class of surfaces, suitable for establishing existence. We finish this talk with Allard's regularity theorem for area minimizers , relating it with the PDE approach in the begining. If time permits we may discuss about optimal regularity results in codimension 1.

Thu 16.01.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Perf(X) vs D^b(X)

Speaker: Federico Barbacovi

Abstract: Smoothness is a central concept in geometry. Whether you are working in algebraic geometry or differential geometry, if your scheme/manifold is not smooth you may have some troubles. When working with derived categories, one finds out that the singularities of a scheme are captured by the difference between perfect complexes and bounded complexes. However, understanding how distant Perf(X) and D^b(X) are is not always an easy task to accomplish. In this talk I will survey the topics mentioned above and introduce the category of matrix factorizations.

Thu 23.01.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Polyhedral Manifolds

Speaker: Tom Sharpe

Abstract: Polyhedral manifolds are in some sense discrete versions of Riemannian manifolds, where metric singularities of conical type are allowed in codimension 2. In this setting, interesting invariants such as curvature and holonomy can be defined and extracted using only finite data. In my talk I will define the key notions in this field, introduce you to special class of polyhedral manifolds, and tell you some things we do and don't know about them.

Thu 30.01.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Cohomogeneity-one manifolds

Speaker: Jakob Stein

Abstract: A natural generalisation of homogeneous spaces, say for a Lie group K, are spaces with a 1-dimensional quotient under a K-action. These are the so-called cohomogeneity-one manifolds, and there are many examples of them. The large degree of symmetry is useful when we consider cohomogeneity-one Riemannian manifolds, with isometric K-actions: cohomogeneity-one metrics have given rise to many examples of Riemannian metrics satisfying special properties e.g. Ricci flat, nearly Kahler. We will see examples, sketch some basic theory, and discuss applications.

Thu 06.02.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: How can geometry help us predict the movement of planets?

Speaker: Tim King

Abstract: Suppose that you have a really big computer, and want to estimate where each of the planets will be in a week's time. I will describe how well you can do (i) if you ignore all the geometry and (ii) if you don't. Happily for geometers, strategy (ii) works out better. This will be an introductory talk which assumes knowledge of differential geometry, but not of Hamiltonian/Lagrangian mechanics.

Keywords: Hamiltonian, Symplectic integrator

Thu 13.02.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Aspherical Complex Surfaces, Proven using CAT(K) metrics

Speaker: Jenny Swinson

Abstract: We will have a look at a family of complex surfaces, obtained as ramified covers of the complex projective plane, ramified at a particularly special line arrangement. These complex surfaces (4-dimensional) have particular topological properties that can be shown by constructing particular singular metrics, zooming in on tangent cones around singular points, and expressing these tangent cones as bundles over...nice, simple 2-(actual)-dimensional surfaces, with spherical metrics and some conical singularities! I will explain all terminology as we go along.

Thu 20.02.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Mean Curvature Flow with Surgeries

Speaker: Albert Wood

Abstract: It is well-known that the proof of the Poincare conjecture was completed using Ricci flow with surgeries, but how was this done, and what are surgeries? In this talk I will explain by analogy, using a theorem of submanifold geometry that is proved via my favourite geometric flow - the mean curvature flow. I will give a quick introduction to this flow, explain what surgery is and what it involves in this context, and deduce a couple of topological theorems.

Thu 27.02.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: t.b.a.

Speaker: t.b.a.

Abstract:

Thu 05.03.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Hyper-Kähler reduction

Speaker: Jaime Mendizabal

Abstract: A Kähler manifold carries Riemannian, complex and symplectic structures, which are compatible in a certain way. Hyper-Kähler manifolds carry a Riemannian structure, plus three complex structures (and symplectic forms) which satisfy the quaternionic relations. In particular, they are Kähler in three (and, in fact, infinitely many) ways, and their tangent spaces are quaternionic. They can also be viewed as having a holomorphic symplectic structure. This can be used to define a quotient of the manifold by a group that preserves the hyper-Kähler structure, in a way analogous to symplectic reduction for symplectic manifolds (or the closely related GIT quotient for Kähler manifolds). We will review symplectic reduction and define hyper-Kähler manifolds and reduction, and will end by show some examples.

Thu 12.03.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: Homogeneous and inhomogeneous hypersurfaces in symmetric spaces

Speaker: Alberto Vazquez Rodriguez

Abstract: A hypersurface is (extrinsically) homogeneous if it is a regular orbit of a cohomogeneity one action. Also, a hypersurface is said to be isoparametric if it and all its nearby equidistant hypersurfaces have constant mean curvature.

We will review some known classification results of these kinds of hypersurfaces in symmetric spaces. In particular, homogeneous hypersurfaces have been classified in symmetric spaces of rank one except in quaternionic hyperbolic spaces, where this problem is equivalent to an involved quaternionic linear algebra problem. ​

In this talk, I will present the classification of homogeneous hypersurfaces and the construction of inhomogeneous isoparametric examples in quaternionic hyperbolic spaces.

Thu 19.03.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: t.b.a.

Speaker: t.b.a.

Abstract:

Thu 26.03.20

17.00-18.15

Location: UCL, Department of Mathematics, 25 Gordon Street, Room 707

Title: t.b.a.

Speaker: Lucía Martín Merchán (Universidad Complutense Madrid)

Abstract:

Thu 04.10.18

17.30-18.30

Location: Imperial College, Sherfield Building, CDT space, Teaching Room 3 (402)

Title: Ouverture: the art of being a blow-up

Speaker: Mirko Mauri

Abstract: The main challenge of modern geometry is to describe or classify high dimensional entities. This poses the serious problem of how to visualize such objects. Although they rarely provides rigorous demonstrations, drawings and pictures are essential in building our intuition. In this opening seminar we will discuss some techniques to visualize complex algebraic varieties. In particular, we will focus on a construction of crucial interest both in algebraic geometry and symplectic topology: the blow-up. We will "see" most of its properties through pictures.

Keywords: blow-up, real trace, algebraic geometry, symplectic topology, tropicalization

Link to video. Link to Slides.

Thu 11.10.18

No seminar

Thu 18.10.18

17.00-18.00

Location: UCL Maths 707

Title: Lie groups, singularities and Springer theory

Speaker: Dougal Davis

Abstract: Complex simple Lie groups are groups of matrices that behave in a similar fashion to the group SL_n(C) of n x n complex matrices of determinant 1. They are classified up to isogeny by a short list of simple graphs, called Dynkin diagrams. In an apparently unrelated theorem, the very same graphs also classify a particular class of singularities on complex algebraic surfaces, called du Val singularities. In this talk, I will briefly explain these two classification theorems. I will then explain how this mysterious combinatorial coincidence is realised directly as a special case of Springer theory, which gives a general method for producing singularities (and resolutions of them) from Lie groups. Time permitting, I will also explain some of the deeper aspects of this correspondence, such as the representation theory hidden within the singularities and resolutions of Springer theory.

Keywords: [Lie theory], [singularities], [algebraic geometry], [representation theory]

Link to video.

Thu 25.10.18

17.00-18.00

Location: UCL Maths D103

Title: Introduction to Intersection Theory

Speaker: Navid Nabijou

Abstract: The cohomology of a smooth algebraic variety X comes equipped with a cup product. If we are given two smooth subvarieties of X, then each of them defines a Poincare dual cohomology class. The cup product of these classes can then be interpreted (under Poincare duality) as a “transverse intersection” of the subvarieties we started with. This makes sense even if the original varieties did not happen to intersect transversely. This notion - of transverse or “generic” intersection - is ubiquitous in algebraic geometry. It forms the cornerstone of modern enumerative geometry, and is central to fields as diverse as birational geometry and the theory of motives. For various reasons, the usual cohomology ring is not well-suited for the aforementioned applications. To start with, it does not behave well for singular varieties, or for varieties defined over fields other than the complex numbers. More crucially, it does not provide a way to construct so-called “refined intersection products”. In this talk I will explain, by means of examples, what the term “refined intersection product” means, and why constructing one is so important and useful. I will then explain the algebro-geometric construction of Fulton-MacPherson, and give some example applications.

Keywords: algebraic geometry, intersection theory, refined intersection, Chow groups

Link to video.

Thu 01.11.18

17.00-18.00

Location: UCL Maths 707

Title: An Introduction to Geometric Flows

Speaker: Albert Wood

Abstract: In this talk, I’d like to show you why geometric flows are exciting and relevant. To do this, I plan on showing you three explicit examples of popular geometric flows (Heat flow, Mean Curvature flow, and Ricci flow), and prove a variety of things with them (existence of geodesics, the Hodge theorem, and the Isoperimetric Inequality). Along the way I’ll provide flow-y art to accompany the mathematics, to accentuate the beauty of the subject!

Keywords:

Link to video (video file is corrupted and cannot be viewed at the moment)

Thu 08.11.18

17.00-18.00

Location: UCL Maths 707

Title: Introduction to Geometric Group Theory with applications to Accessibility

Speaker: David Sheard

Abstract: Geometric group theory aims to study groups using tools from geometry and topology, more precisely to study finitely generated groups by looking at the way they act on geometric and topological spaces. In this talk I shall introduce some of the aims of geometric group theory, and construct a well-known space associated to a finitely presented group. I will talk about algebraic splittings of groups in the sense of van Kampen's Theorem, and finish by sketching the proof of Dunwoody's theorem that finitely presented groups admit only a finite number of such splittings over finite subgroups.

Keywords: geometric group theory; fundamental group, finitely presented group, accessibility of groups; simplicial complex; group action

Link to video.

Thu 15.11.18

17.00-18.00

Location: UCL Maths D103

Title: Introduction to Derived Categories

Speaker: Vladimir Eremichev

Abstract: Derived categories were discovered by Grothendieck and Verdier in 1960s and have since then became an ubiquitous tool in homological algebra and its applications to algebraic geometry, number theory, and other parts of mathematics. This talk will be a gentle introduction to the subject, based on lots of examples and very few proofs. We will start by overviewing the basics of categories, concentrating on our main examples: modules over a ring and coherent sheaves over a variety. We will then construct the corresponding derived categories and see how they greatly simplify many `scary' concepts, like Tors, Exts, spectral sequences and so on. If time permits, we will also explore how the geometry of a variety is encoded within its derived category. No prior knowledge of categories or derived functors is necessary!

Keywords: derived categories, derived functors, duality, cohomology, spectral sequence, birational geometry, canonical bundle, six functors

Thu 22.11.18

17.00-18.00

Location: UCL Maths 707

Title: Exceptional Holonomy: The Groups G2 and Spin(7)

Speaker: Fabian Lehmann

Abstract: The holonomy group of a Riemannian manifold describes parallel transport of vectors around closed loops. It is closely related to the curvature of the metric. In 1953 Berger gave a classification of all groups which can be the holonomy group of irreducible and nonsymmetric Riemannian metrics. Two of the groups in the classification, G2 and Spin(7), have been termed the exceptional holonomy groups as metrics with these holonomy groups are particularly hard to find. I will give a thorough introduction to these two groups.

Keywords: #Differential Geometry #Riemannian Geometry #Holonomy #G2 #Spin(7) #Quaternions #Octonions

Thu 29.11.18

17.00-18.00

Location: UCL Maths D103

Title: A Horizontal Introduction to Stacks

Speaker: Damián Gvirtz

Abstract: Algebraic stacks are an enlargement of the category of schemes. They most naturally appear whenever the problem of "too many automorphisms" prevents the existence of moduli spaces, e.g. for parameter spaces of curves. Instead of engaging in a hand-waving story, my talk will focus on the technical machinery behind stacks so that when the time comes you can say "quasi-separated Deligne-Mumford stack" with confidence.

Keywords: fine moduli space, Grothendieck topology, 2-category, descent theory

Thu 06.12.18

17.00-18.00

Location: UCL Maths 707

Title: Picard-Lefschetz fibrations

Speaker: Angela Wu

Abstract: Picard-Lefschetz Theory (the complex analogue of Morse Theory) was first invented for complex surfaces by Emile Picard, then generalized to higher dimensions by Solomon Lefschetz (who by the way had no hands). It studies Lefschetz fibrations: smooth proper maps from smooth oriented 2n-manifolds to the complex numbers which have finitely many isolated and non-degenerate critical points. Just like in Morse Theory, interesting things happen to the fibres of these maps near the critical values that we can use to deduce interesting things about our original manifold. And what's more, it turns out that Picard-Lefschetz Theory is, in some sense, essentially a symplectic phenomenon. In this talk, I'll introduce you to Lefschetz fibrations and show you some reasons why they are so very useful in Symplectic Geometry.

Keywords: symplectic geometry, Lefschetz fibration, monodromy, Dehn twist, vanishing cycle

Thu 13.12.18

17.00-18.00

Location: UCL Maths D103

Title: A journey towards Mirror Symmetry

Speaker: Enrica Mazzon

Abstract: The main characters of this talk are Calabi-Yau manifolds. After showing their relevance in the study of manifolds, I will explain their relation to Mirror Symmetry, a fast-moving research area at the boundary between mathematics and theoretical physics. Originated from observations in string theory, Mirror Symmetry suggests that Calabi-Yau manifolds should "come in pairs": I will explain what this means geometrically.

Keywords: Calabi-Yau, quintic 3-fold, Mirror Symmetry, SYZ conjecture

Thu 10.01.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Nearly Kähler six-manifolds with two-torus symmetry

Speaker: Giovanni Russo

Abstract: We consider nearly Kähler six-manifolds with a two-torus symmetry. We construct a multi-moment map for the torus action and describe its general properties. At regular values, the action is necessarily free on the level sets and determines the geometry of three-dimensional quotients. Finally we give a result on an inverse construction producing nearly Kähler six-manifolds from three-dimensional data.

Keywords: nearly Kähler, multi-moment maps, two-torus symmetry

Thu 17.01.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Classification of simple singularities

Speaker: Erik Paemurru

Abstract: We consider complex algebraic varieties and analytic spaces. We say two singularities are "equivalent" if they are biholomorphic in a neighbourhood of the singular points. A singularity of the hypersurface f = 0 is "simple" if we only get finitely many equivalence classes of singularities when changing the coefficients of f slightly. I will give a proof of the classical result that simple singularities are precisely the ADE-singularities, which are Du Val singularities in the surface case.

Keywords: Milnor number, right-equivalence, contact-equivalence, splitting lemma

Link to video.

Thu 24.01.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Introduction to Twistor Theory

Speaker: Benjamin Aslan

Abstract: In this talk, we will learn in which way twistor theory builds a bridge between Riemannian and complex geometry. More precisely, every even-dimensional Riemannian manifold M can be equipped with a twistor space which parametrises certain almost complex structures on M. When M is four-dimensional, the twistor space can itself be equipped with two canoncial almost structures. We will learn how properties about these structures translate into properties of the Riemannian structure of M.

Keywords:

Link to video.

Thu 31.01.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Many reasons to fear the Grothendieck ring of varieties

Speaker: Luigi Lunardon

Abstract: The Grothendieck ring of varieties is an interesting and mysterious ring. In this talk, we introduce it and try to understand something more about its properties. We see how some of its algebraic properties are closely related to many interesting geometric problems. For instance, if the class of the affine line was not a zero-divisor in this ring, it was possible to conclude that the cubic fourfold was rational. Moreover, if this was not enough, we present further geometric reasons to motivate the interest in it. After we have risen your hope that this may actually prove some conjectures, we show that the class of the affine line is a zero-divisor in the Grothendieck ring. Hopefully, even after this shocking revelation, your life will continue as usual; but you will know why this ring is something to be scared of.

Keywords: Grothendieck ring of varieties, class of the affine line, zero divisor, stable birationality, Calabi-Yau

Link to video.

Thu 07.02.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Intersections of secant varieties to algebraic curves

Speaker: Mara Ungureanu

Abstract: For a smooth projective curve, the varieties parametrising its secant planes are among the most studied objects in classical enumerative geometry. In order to better understand their geometry, which in turn describes the extrinsic properties of the curve, one is lead to the study of Brill-Noether theory. This allows us to translate such extrinsic geometry problems in terms of objects belonging to the intrinsic geometry of the curve, namely subvarieties of its symmetric product. In this talk we shall introduce some basic notions of Brill-Noether theory, define secant varieties to a curve embedded in projective space and study some unexpected properties of their geometry that arise as non-transversality of intersections inside the symmetric product of the curve.

Keywords: enumerative geometry, algebraic curves, symmetric product, secant planes, Brill-Noether theory

Link to video.

Thu 14.02.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: The Topology of 4-Manifolds with Finite Fundamental Group

Speaker: Johnny Nicholson

Abstract: In the 1980s Freedman and Quinn showed that techniques from high-dimensional topology, such as surgery theory and the s-cobordism theorem, can be made to work for topological 4-manifolds. Whilst these techniques can be used to classify simply-connected topological 4-manifolds, similar results in the non-simply connected case are few and far between. This is largely due to the mystery surrounding the second homotopy group \pi_2(M) which has the structure of a \Z[\pi_1(M)] module. In this talk, we will give an overview of two approaches to the classification of 4-manifolds using techniques from high-dimensional topology. The first approach is to start by classifying up to homotopy and then to use classical surgery to classify up to homeomorphism within each homotopy type. Whilst a clean homotopy classification can often be obtained, the second step throws up obstructions which can only be computed for a small class of groups. The second approach, which also works for smooth 4-manifolds, is to first classify up to connected sum with S^2 \times S^2 using Kreck’s modified surgery and then to deal with the cancellation of the (S^2 \times S^2)-summands separately. In the 1990s, Hambleton and Kreck explored the connection between this cancellation problem and the problem of cancellation of a free summand in a \Z[\pi_1(M)] module and the cancellation of a wedge with S^2 in a finite two-complex. This led to a complete classification of topological 4-manifolds with cyclic or odd-order fundamental group. I will report on recent progress made on the cancellation problem for modules and complexes, and will discuss a current project to extend the known examples of non-cancellation for manifolds, i.e. examples of 4-manifolds M and N for which M \# (S^2 \times S^2) = N \# (S^2 \times S^2) but for which M and N are not even homotopic.

Keywords: Manifolds, CW-complexes, modules, surgery theory, group homology, cancellation

Link to video.

Thu 21.02.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Ricci Flow in Milnor Frames

Speaker: Syafiq Johar

Abstract: In this talk, we are going to talk about the Type I singularity on 4-dimensional manifolds foliated by homogeneous S3 evolving under the Ricci flow. We review the study on rotationally symmetric manifolds done by Angenent and Isenberg as well as by Isenberg, Knopf and Sesum. In the latter, a global frame for the tangent bundle, called the Milnor frame, was used to set up the problem. We shall look at the symmetries of the manifold, derived from Lie groups and its ansatz metrics, and this global tangent bundle frame developed by Milnor and Bianchi. Numerical simulations of the Ricci flow on these manifolds are done, following the work by Garfinkle and Isenberg, providing insight and conjectures for the main problem. Some analytic results will be proven for the manifolds S1×S3 and S4 using maximum principles from parabolic PDE theory and some sufficiency conditions for a neckpinch singularity will be provided. Finally, a problem from general relativity with similar metric symmetries but endowed on a manifold with different topology, the Taub-Bolt and Taub-Nut metrics, will be discussed.

Keywords: Ricci flow, Milnor frames, maximum principle, parabolic system of PDEs

Link to video.

Thu 28.02.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: The spaces of stability conditions of the Kronecker quiver

Speaker: Caitlin McAuley

Abstract: It is well known that the space of stability conditions of a triangulated category is a complex manifold. In fact, mirror symmetry predicts that this space carries a richer geometric structure: that of a Frobenius manifold. From a quiver, one can construct a sequence of triangulated categories which are indexed by the integers. It is then natural to study the stability manifolds of these categories, and in particular to consider any changes to the manifolds as the integer indexing the triangulated category varies. We will study this construction for the Kronecker quiver, and discuss how the results provide evidence for a Frobenius structure on these stability manifolds

Keywords: stability conditions, quiver representations, triangulated categories, Frobenius manifolds

Link to video.

Thu 07.03.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: What's so special about the Lagrangian angle?

Speaker: Christopher Evans

Abstract: The mean curvature of a submanifold is a notoriously irritating quantity to compute. For Lagrangian submanifolds of Calabi-Yau manifolds however, there is a better way. In this talk, we will introduce a function called the Lagrangian angle and see how it determines the mean curvature. We'll also try and generalise our discussion to non-flat manifolds and see some of the problems therein.

Keywords:

Link to video.

Thu 14.03.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Contraction Algebras and the Homological Minimal Model Program

Speaker: Jenny August

Abstract: Contraction algebras are a class of finite dimensional algebras introduced by Donovan and Wemyss as a tool to study minimal models of 3-folds or more generally, flopping contractions. In this talk, I will give an introduction to these algebras, including the key conjecture in this area which states that the derived category of such an algebra completely controls the associated geometry. I will then go on to give evidence towards this conjecture by providing a complete description of the derived equivalence class of these algebras.

Keywords: derived category, flopping contractions, tilting complexes

Thu 21.03.19

17.00-18.00

Location: Bush House South East Wing 1.05

Title: Seminar cancelled

Speaker:

Abstract:

Keywords:

Thu 25.04.19

17.00-18.00

Location: UCL, Gordon Street 25, Room: Maths 505

Title: Geometric Structure of Moduli Spaces of Morse-Smale Flows and Manifolds with Analytical Corners

Speaker: Yixuan Wang

Abstract: In 1857 Riemann observed that an isomorphism class of compact Riemann surfaces of genus g has (3g-3) parameters, which he named "die Moduln dieser Klasse" (the moduli of the class). The concept of moduli as parameters finds itself in geometry, where understanding the parameter space of objects and the variation of an object are often times vital. These moduli problems generate novel geometric structures, too. In this talk we shall see an illustrated study of moduli spaces of generic Morse-Smale flows, with a brief introduction to theories of manifolds with strange corners (so-called analytical corners in particular), and a new result on linearizing certain vector fields (analytical Morse's Lemma).

Keywords: moduli problem, Morse theory, manifold with corners, analytical Morse's Lemma

Thu 02.05.19

17.00-18.00

Location: UCL, Gordon Street 25, Room: Maths 505

Title: A taste of categorical geometry

Speaker: Bradley Doyle

Abstract: I will aim to give a brief overview of two connected ideas related to algebraic geometry and category theory. First I will give an informal description of a derived category and introduce semiorthogonal decompositions. I will give a few examples as well as mentioning some of the main results. Then I will talk about categorical or noncommutative resolutions. Kuznetsov showed a connection between categorical resolutions and semiorthogonal decompositions which I will explain. Time permitting I will finish by mentioning noncommutative resolutions for quotients by reductive groups.

Keywords: algebraic geometry, category theory, derived category, semiorthogonal decomposition, noncommutative resolution

Thu 09.05.19

17.00-18.00

Location: UCL, Gordon Street 25, Room: Maths 505

Title: Homological stability for Artin monoids

Speaker: Rachael Boyd

Abstract: Many sequences of groups satisfy a phenomenon known as homological stability. In my talk, I will report on recent work proving a homological stability result for sequences of Artin monoids, which are monoids related to Artin and Coxeter groups. From this, one can conclude homological stability for the corresponding sequences of Artin groups, assuming a well-known conjecture in geometric group theory called the K(\pi,1)-conjecture. This extends the known cases of homological stability for the braid groups and other classical examples. I will give a gentle introduction to Coxeter and Artin groups, homological stability and the K(\pi,1)-conjecture, before stating my results.

Keywords: Homology, group homology, classifying space

Thu 16.05.19

17.00-18.00

Location: UCL, Gordon Street 25, Room: Maths 505

Title: Introduction to Geometric Deep Learning

Speaker: Mehdi Bahri

Abstract: Machine Learning and Deep Learning have had a profound impact on artificial intelligence. Most of the research so far has focused on Euclidean data (images, sound, text), and even though impressive results have been achieved on many applications, important types of data cannot be processed with traditional machine learning algorithms due to their non-Euclidean structure: graphs (e.g., molecules, social networks), and manifolds (e.g., 3D shapes). This talk introduces the emerging field of Geometric Deep Learning, a novel branch of machine learning aimed at developing non-Euclidean extensions of Deep Learning algorithms. We will present motivating examples, review past and recent approaches, and touch on the future challenges and research directions in the field.

Keywords: Convolution, Convolutional Neural Networks, Graphs, Manifolds

Thu 23.05.19

17.00-18.00

Location: UCL, Gordon Street 25, Room: Maths 505

Title: Homological Mirror Symmetry for Invertible Polynomials

Speaker: Matthew Habermann

Abstract: In this talk I will describe the statement and significance of homological mirror symmetry for Landau-Ginzburg models. Specifically, I will focus on invertible polynomials, which give rise to a (perhaps more-than-usual) mysterious relationship between the algebraic geometry of singularities, and the symplectic geometry of Lefschetz fibrations. I will then describe recent advances in the subject through examples, emphasising the novelty of the techniques used.

Keywords: A_\infty structures, moduli space, quiver, Fukaya-Seidel category, matrix factorisation

Thu 30.05.19

17.00-18.00

Location: UCL, Gordon Street 25, Room: Maths 505

Title: Generic vanishing theorems and applications

Speaker: Fabio Bernasconi

Abstract: Green and Lazarsfeld discovered a Kodaira type vanishing theorem for general topologically trivial line bundles on abelian varieties over the complex numbers. This has been further refined in work by Hacon, Pareschi, Popa and Schnell by introducing the notion of GV sheaf. In this talk, I would like to explain the statement of the generic vanishing theorem and their formulation via derived category machinery. The goal would be to give a sketch of a proof by Hacon and Chen on the birational characterisation of abelian varieties.

Keywords: generic vanishing, Fourier-Mukai transforms, abelian varieties

Thu 06.06.19

17.00-18.15

Location: UCL, Gordon Street 25, Room: Maths 505

Title: Deep Learning on graphs: a journey from continuous manifolds to discrete networks

Speaker: Michaël Defferrard

Abstract: This talk will discuss learning and processing with structured data. Structured data appears in many applications: the pixels of an image are structured by a grid, weather measurements are structured by the Earth's geometry, the atoms of a molecule are structured by chemical forces, economic and demographic indicators are structured by transportation networks. Graphs will be our preferred representation of structure. We will start with the modeling of sampled manifolds by graphs, and see how the graph Laplacian converges to the Laplace-Beltrami. As an example, we'll consider the classification of cosmological observations on the sphere. We'll then move on to purely discrete domains, where the absence of a strong theory leaves freedom in the design of computational operations. After the reinterpretation of our Laplacian-based tool in a more general framework, the passing and aggregation of information across vertices, we will see some alternative formulations. As an example we'll consider the classification of scientific papers given their content and relations, defined by a citation network.

Keywords: