RadialPlotter: a Java application for fission track, luminescence and other radial plots
with zj a transformation of some data and σ(zj) the corresponding measurement uncertainty. For example, if zj
= log(tj) then σ(zj) = σ(tj)∕tj. z0 is a convenient central value such as the weighted mean. The slope of a line
connecting the origin (x=0,y=0) of a radial plot with a data point (xj,yj) equals zj, and the horizontal
distance along x-axis is a measure if its precision. Thus, the radial plot simultaneously visualises a
measurement’s value and precision. No other graphical method achieves this goal with the same elegance
(Galbraith, 1988). This makes the radial plot the method of choice for visualising heteroscedastic data,
i.e. data with (large and) variable measurement uncertainties. Traditional applications in the Earth
Sciences are fission track and luminescence dating, which are governed by Poisson processes (e.g.,
Galbraith, 1990; Galbraith et al., 1999). In principle, however, radial plots can be used for any kind of
data.
RadialPlotter is a user-friendly application for generating radial plots. It has the following advantages over
existing programs such as Trackkey or MacTrack. (1) The program was developed solely for radial plots and does
not perform other functions for data reduction or interpretation. Therefore, radial plot functions are not buried deep
inside the menu structure and the interface is very straightforward. (2) RadialPlotter was written in Java (version
5) and is, therefore, perfectly platform independent. (3) In addition to fission track radial plots, RadialPlotter also
offers the possibility to generate radial plots for luminescence dating, or any other kind of data such as (U-Th)/He
or 40Ar/39Ar ages.
RadialPlotter can be downloaded free of charge from http://pvermees.andropov.org/radialplotter. The
program consists of a single executable jar file (RadialPlotter.jar). This makes installation straightforward: it
suffices to download and open this file to run RadialPlotter. For testing purposes, three example input files are
provided on the website, one for each of the three possible input formats (‘Fission Tracks’, ‘Luminescence’ and
‘Other’). The graphical output can be saved as either bitmap or vector images, in a .png or .pdf
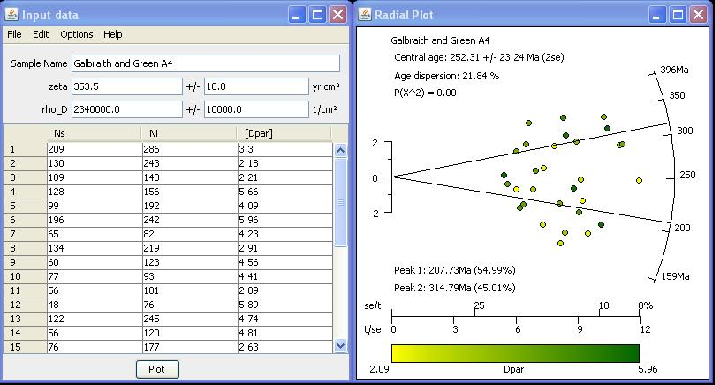
format, respectively. RadialPlotter automatically performs a χ2-test for statistical homogeneity of
fission track data. For populations that have failed this test, the program implements the mixture
modeling algorithm of Galbraith and Green (1990)(Figure 1). Data points can be colour-coded to show an
additional variable such as chemical composition or a kinetic parameter. Colour-coding can also be a useful
tool for double-dating, which is rapidly gaining popularity in detrital studies (e.g., Campbell et al.,
2005). For example, the U-Pb ages of double-dated zircons could be shown as colours on a (U-Th)/He
radial plot. Hopefully, this kind of flexibility will give the radial plot the wider user base which it
deserves.
References
- Campbell,
- I. H., Reiners, P. W., Allen, C. M., Nicolescu, S., Upadhyay, R., 2005: He-Pb double dating of detrital zircons from the Ganges and Indus Rivers: Implication for quantifying sediment recycling and provenance studies, Earth and Planetary Science Letters 237, 402-432.
- Galbraith,
- R. F., 1988: Graphical display of estimates having differing standard errors, Technometrics, 30, 271-281.
- Galbraith,
- R. F., 1990: The radial plot: graphical assessment of spread in ages, Nuclear Tracks and Radiation Measurements, 17, 207-214.
- Galbraith,
- R. F. and Green, P. F., 1990: Estimating the component ages in a finite mixture, Nuclear Tracks and Radiation Measurements, 17, 197-206.
- Galbraith,
- R. F., Roberts, R. G., Laslett, G. M., Yoshida, H. and Olley, J. M., 1999: Optical dating of single and multiple grains of quartz from Jinmium rock shelter, northern Australia: Part I, experimental design and statistical models, Archaeometry, 41, 339-364.