Nature inspired methods for optimization
A Julia primer for process engineering

| Author | Eric S Fraga (email) |
| DOI | 10.5281/zenodo.7016482 |
| Latest news | First edition published |
| Git revision | 2022-11-09 1a40907 |
An ebook (PDF) version of this book is available from leanpub
©
2022
Eric S Fraga, all rights reserved.
Sargent Centre for Process Systems Engineering
Department of Chemical Engineering
University College London (UCL)
Dedicated to Jennifer and Sebastian, with love.
- DOI
- 10.5281/zenodo.7016482
- First edition
- 2022-08-19
- Current version
- 2022-11-09 1a40907
Nature inspired methods for optimization have been available for many years. They are attractive because of their inspiration and because they are comparatively easy to implement. This book aims to illustrate this, using a relatively new language, Julia. Julia is a language designed for efficiency. Quoting from the developers of this language:
Julia combines expertise from the diverse fields of computer science and computational science to create a new approach to numerical computing. [Bezanson et al. 2017]
The case studies, from industrial engineering with a focus on process engineering, have been fully implemented within the book, bar one example which uses external codes. All the code is available for readers to try and adapt for their particular applications.
This book does not present state of the art research outcomes. It is primarily intended to demonstrate that simple optimization methods are able to solve complex problems in engineering. As such, the intended audience will include students at the Masters or Doctoral level in a wide range of research areas, not just engineering, and researchers or industrial practitioners wishing to learn more about Julia and nature inspired methods.
Table of Contents
1. Introduction
1.1. Optimization
The problems considered in this book will all be formulated as the minimization of the desired objectives. There may be one or multiple objectives. In either case, the general formulation is
\begin{align} \label{org5094869} \min_{d \in \mathcal{D}} z &= f(d) \\ g(d) & \le 0 \nonumber \\ h(d) & = 0 \nonumber \end{align}where \(d\) are the decision (or design) variables and \(\mathcal{D}\) is the search domain for these variables. \(\mathcal{D}\) might be, for instance, defined by a hyper-box in \(n\) dimensional space, \[ \mathcal{D} \equiv \left [ a, b \right ]^n \subset \mathbb{R}^n \] when only continuous real-valued variables are considered. More generally, the problem may include integer decision variables. Further, the constraints, \(g(d)\) and \(h(d)\), will constrain the feasible points within that domain.
1.2. Process systems engineering
The focus of this book is on solving problems that arise in process systems engineering (PSE). Optimization plays a crucial part in many PSE activities, including process design and operation. The problems that arise may have one or more of these challenges, in no particular order:
- nonlinear models
- multi-modal objective function
- nonsmooth and discontinuous
- distributed quantities
- differential equations
- small feasible regions
- multiple objectives
Each of these aspects, individually, can prove challenging for many optimization methods, especially those based on gradients to direct the search for good solutions. Some problems may have several of these characteristics.
Three chapters will present example design problems which exhibit some of the above aspects:
- purification section for a chlorobenzene production process: discontinuous, non-smooth, small feasible region;
- design of a plug flow reactor: continuous distributed design variable with behaviour described by differential equations;
- heat exchanger network design: combinatorial, non-smooth, complex problem formulation.
These problems may be challenging for gradient based methods and therefore motivate the use of meta-heuristic methods. In this book, I will present meta-heuristic methods inspired by nature.
1.3. Nature inspired optimization
There are many optimization methods and different ways of classifying these methods. One classification used often is deterministic versus stochastic. The former include direct search methods [Kelley 1999] and what are often described as mathematical programming, such as the Simplex method [Dantzig 1982] for linear problems and many different methods for nonlinear problems [Floudas 1995]. The main advantage of deterministic methods is that they will obtain consistent results for the same starting conditions and may provide guarantees on the quality of the solution obtained and/or the performance of the method, such as speed of convergence to an optimal solution. If you are interested in using Julia for mathematical programming, the JuMP package is popular.
Stochastic methods, as the name implies, are based on random behaviour. The main implication is that the results obtained will vary from one attempt to another, subject to the random number generator used. However, the advantage of stochastic methods can be the ability to avoid getting stuck in local optima and potentially find the global optimum or optima for the problem.
Some popular stochastic methods include simulated annealing [Kirkpatrick et al. 1983] and genetic algorithms [Holland 1975] but many others exist [Lara-Montaño et al. 2022]. Simulated annealing, as the name implies, is based on the process of annealing, typically in the context of the controlled cooling of liquid metals to achieve specific properties (hardness, for instance). Genetic algorithms mimic Darwinian evolution, for instance, by using survival of the fittest to propagate good solutions and evolve better solutions. One common aspect of many stochastic methods is that they are inspired by nature.
In this book, we will consider three such nature inspired optimization methods: genetic algorithms, particle swarm optimization [Kennedy and Eberhart 1995], and a plant propagation algorithm [Salhi and Fraga 2011]. These are chosen somewhat arbitrarily as examples of stochastic methods. The selection is in no way intended to indicate that these are the best methods for any particular problem. The aim is to illustrate the potential of these methods, how they may be implemented, and how they may be used to solve problems that arise in process systems engineering.
1.4. Literate programming
This book includes all the code implementing the nature inspired optimization methods and most of the case studies, sufficient to allow readers to attempt the problems themselves.
Programming is at heart a practical art in which real things are built, and a real implementation thus has to exist. [Kay 1993]
The book has been written using literate programming [Knuth 1984]. The motivation for literate programming, to quote Donald Knuth, comes from:
[…] the time is ripe for significantly better documentation of programs, and that we can best achieve this by considering programs to be works of literature. [Knuth 1984]
Therefore, this book may be considered to be the documentation of the code used to implement the methods and to evaluate the problems defined in the case studies. The code presented in the book is automatically exported to the source code files, suitable for immediate invocation.
The technology supporting literate programming in this case is org mode (version 9.5.4). Org mode is a special mode in the Emacs editor (version 29.0.50.0). Org mode supports code blocks which may include programming code in a very wide range of languages. These code blocks are tangled into code files [Schulte and Davison 2011]. In the case of this book, all the code can be found in the author's github repository.
As well as enabling tangling to create the source code files, org mode supports exporting documents to a variety of different targets, including PDF, epub, and HTML. The HTML version of the book is freely available.
Lastly, the literate programming support in org mode not only enables tangling, it also allows for code to be run directly within the Emacs editor while editing the document, with the results of the evaluation inserted into the document [Schulte and Davison 2011]. This book makes full use of this capability to process the results of the optimization problems, including extracting and generating statistical data with awk, grep, and similar tools, and plotting the outcomes with gnuplot.
1.5. The Julia language
Julia is a multi-purpose programming language with features ideally suited for writing generic optimization methods and numerical algorithms in general. To repeat the quote from the initial authors of the language,
Julia combines expertise from the diverse fields of computer science and computational science to create a new approach to numerical computing.[Bezanson et al. 2017]
For the purposes of this book, the key features of Julia are the following:
dynamic typing for high level coding;
multiple dispatch to create generic code that may be easily extended;
functional programming elements for operating on data easily;
integrated package management system to enable re-use and distribution; and,
the REPL (read-evaluate-print loop) for exploring the language and testing code.
In this section, some of these aspects will be illustrated through code elements that will be used by all the nature inspired optimization methods presented in this book.
Julia version 1.7 has been used for all the codes in this book. I have tried to ensure that the style guide for writing Julia code has been followed throughout.
1.5.1. The package and modules
The codes presented in this book are tangled into a Julia package called NatureInspiredOptimization and available from the author's github repository. This package can be added to your own Julia installation by entering the package manager system in Julia using the ] key and then using the add command with the URL of the git repository for the package. This will add not only the package specified but also any dependencies, i.e. other packages, specified by this package. Hitting the backspace key will exit the package manager. Once added, the package and any sub-packages it may define, can be accessed through the using Julia statement. This will be illustrated in the examples in this book.
Some external packages have been used in writing the code presented in the book. These include DifferentialEquations, Plots, JavaCall, and Printf. These will automatically be installed when installing the NatureInspiredOptimization package. The one exception is the Jacaranda package (see Section 3.2 below), written by the author and not currently registered in the Julia Registry. Therefore, this package needs to be added explicitly.
In summary, installing the NatureInspiredOptimization package can be achieved as follows:
$ julia julia> ] pkg> add https://gitlab.com/ericsfraga/Jacaranda.jl pkg> add https://github.com/ericsfraga/NatureInspiredOptimization.jl [...] (@v1.7) pkg> BACKSPACE julia> ^d $
Note that the Jacaranda package is found in a gitlab repository while the NatureInspiredOptimization package is on github.
1.5.2. Objective function
All optimization problems in this book will define an objective function. The methods implemented will all be based on the same signature for the objective function:
(z, g) = f(x; π)
where \(f\) is the name of the function implementing the objective function for the optimization problem, to be evaluated at the point \(x\) in the search space. The second optional argument, \(\pi\), will consist of a data structure of any type which includes parameters that are problem dependent. The function \(f\) is expected to return a tuple. The first entry in the tuple, \(z\), is the value of the objective function for single objective problems and a vector of values for multi-objective problems. The second element of the tuple, \(g\), is a single real number which indicates the feasibility of the point \(x\): \(g\le 0\) means the point is feasible; \(g>0\) indicates an infeasible point, with the magnitude of \(g\) ideally representing the amount of constraint violation, when this is possible. In determining the fitness of a point, see Section 2.2.3 below, both the value(s) of \(z\) and \(g\) will be used.
To allow for both single and multi-objective problems in the code that follows, the generic comparison operators \(\succ\) (\succ in Julia) and ≽ (\succeq in Julia) will be used. \(a \succ b\) means that \(a\) is better than \(b\) and \(a \succeq b\) means that \(a\) is at least as good as \(b\). For single objective minimization problems, which will be the case for the case studies presented later in the book, these operators correspond to the less than (<) and less than or equals (≤) comparisons:
1:≻(a :: Number, b :: Number) = a < b2:≽(a :: Number, b :: Number) = a ≤ b3:export ≻, ≽
This code segment illustrates several Julia features:
- the single line definition of a function using assignment;
- the definition of a binary operator so that ≻ or ≽ can be used as in
a≻bto compareaandb; - the use of generic types so that the same operator can be used for real valued numbers, integers, or combinations of these; and,
the use of
exportto make the operator available without needing to qualify it with the package name.
For multi-objective problems, the value \(z\) returned by the objective function will be a vector of values. When comparing multi-objective solutions, the comparison is based on dominance: a solution dominates another solution if the first one is at least as good in each individual value and strictly better for at least one value:
1: dominates(a, b) = all(a .≽ b) && any(a .≻ b)
This illustrates the use of broadcast, the dot operator, which asks Julia to apply the operator (or function) that follows the dot to each individual element in turn. So this code says that \(a\) dominates \(b\) if all the values of \(a\) are at least as good as the corresponding values of \(b\) and if any value of \(a\) is better than the corresponding value of \(b\).
Given the definition of dominance, we can now define an operator for comparison:
1: ≻(a :: Vector{T}, b :: Vector{T}) where T <: Number = dominates(a,b)
The important feature of this code is that we have defined the function to works for vectors so long as
- they are of the same type,
T, and - the type
Trepresents a number entity, such asFloat64orInt32.
Julia has a hierarchy of types defined.
The multiple dispatch feature of Julia will ensure that the proper comparison function is invoked when comparing objective function values for different points in the search.
1.5.3. Multiprocessing
An additional capability of Julia is multiprocessing, using multiple computers or computer cores simultaneously. Given the increasing prevalence of multi-core systems, including both desktop computers and laptops, it is reasonable to consider writing all code to make use of the extra potential computational power available.
In Julia, the Threads package which is part of the base system provides an easy to use interface to enable the use of multiple cores. The simplest construct, which I will be using in this book, is:
1:Threads.@threads for x ∈ acollection2:# do something(x)3:end
This executes the body of the for loop in parallel using as many threads as made available to Julia. Invoking Julia with the -t option tells Julia how many cores to use simultaneously:
julia -t N
where N is some number, usually less than or equal to the number of cores available on the computer, or by
julia -t auto
In this case, Julia itself will determine the number of cores to use automatically.
The advantage of the nature inspired optimization methods I will be presenting later in this book is that they are all based on populations of solutions. Therefore, the computation associated with the members of the population are easy to distribute amounts the computational cores available. The plant propagation algorithm implementation (see Section 2.5) uses threads to evaluate members of the new population in parallel.
1.6. Representation
Different mathematical problem formulations of the same problem may have an impact on the solution process. Examples exist for the Simplex method [Hall and McKinnon 2004]. The choice of formulation may be a consideration for some problems. Further, for a given formulation, there may be alternative representations of the decision variables [Fraga et al. 2018] and these may affect the performance of individual optimization methods. Tailoring the formulation or representation to the method used may prove beneficial [Salhi and Vazquez-Rodriguez 2014].
For a given formulation, the representation should be chosen taking into account the following considerations:
- The representation should be suitable for the optimization method or methods, enabling the implementation of the appropriate operations that are required by the methods. For instance, if the method is a genetic algorithm, the representation should be suitable for cross-over and mutation operators.
- The representation should cover the complete space of feasible solutions to the problem or, at worst, ensure that the desirable potential solutions can be represented.
- On the other hand, the representation should minimise the probability of the method's operators generating infeasible or undesirable solutions.
Multiple dispatch in Julia aids the process of considering different representations. For instance, different versions of the objective function implementation can be written that differ in the type of the first argument. This enables alternative representations without needing to change the implementation of the solution method. An example of this appeared recently [Fraga 2021c]. This latter example includes code in Julia using the Fresa implementation of a plant propagation algorithm [Fraga 2021b; Fraga 2021a] (see Section 2.5).
2. Nature inspired optimization methods
2.1. Introduction
This book considers a selection of nature inspired optimization methods, specifically a selection of methods which are based on the evolution of a population of solutions. Three different solvers are described and fully implemented. These three have been selected as being representative of the class of evolutionary population based methods but the selection is not meant to be comprehensive, merely illustrative. The implementations presented in the book have been motivated by presentation and pedagogical advantages as opposed to aiming for the most efficient or feature-full implementations. References to production codes will be made where available. However, the codes presented are fully working implementations, as will be demonstrated through application to each of the case studies included in this book.
The three methods presented are
- genetic algorithm, inspired by Darwinian evolution and survival of the fittest;
- particle swarm optimization, inspired by flocks of birds and swarms of bees, looking for food or resting places; and,
- plant propagation algorithm, inspired by the propagation method used by Strawberry plants.
All three methods fundamentally follow the same basic approach, illustrated in Algorithm 1.

2.2. Shared functionality
All the methods presented in this chapter share some common functionality. This functionality is implemented in this section as a set of generic functions. These include fitness calculations for all the methods, including both single objective and multi-objective problems, selection procedures for those methods that use selection, and population management including function evaluation.
The codes in this section assume implicitly that the target optimization problem is one of minimization. If the problem considered were to be one of maximization, transformations of the objective function would be required. Many such transformations are possible including simply negating the value of the objective function.
2.2.1. Generic support functions
Some utility functions are defined in this section to aid in subsequent programming.
mostfitfind the most fit individual in the population and return that individual. As there may be more than one individual in the population with the same maximum fitness value, only the first one is returned. This is arbitrary but given the stochastic nature of the nature inspired optimization methods, it is not unreasonable.
1:
mostfit(p,ϕ) = p[ϕ .≥ maximum(ϕ)][1]φ is the vector of fitness values, a value for each member of the population
p.nondominatedreturn, from a population, those points which are not dominated.
1:
function nondominated(pop)2:nondom = Point[]3:for p1 ∈ pop4:dominated = false5:for p2 ∈ pop6:if p2 ≻ p17:dominated = true8:break9:end10:end11:if ! dominated12:push!(nondom, p1)13:end14:end15:nondom16:endThe key line in this code is line 6. This uses the previously defined better than operator to identify solutions that are dominated by others in the population. Note that this function is primarily intended for use for multi-objective optimization problems, the use of the ≻ operator, and multiple dispatch in Julia, results in code that works for single objective optimization problems as well.
printpointsprint out, row by row, the set of points in a population. As we are using
org modefor writing this book, it is helpful to have the output generated in a form that is convenient for post-processing in that mode.1:
function printpoints(name, points)2:println("#+name: $name")3:for p ∈ points4:printvector("| ", p.x, "| ")5:printvector("| ", p.z, "| ")6:printvector("| ", p.g, "| ")7:println()8:end9:endprintvectorprint, in compact form, the vector of real values, to be used mostly for demonstrator and test codes.
1:
function printvector(start, x, separator = "")2:@printf "%s" start3:for i ∈ 1:length(x)4:@printf "%.3f %s" x[i] separator5:end6:end- randompoint
It is often necessary to generate random points within the search domain. For instance, most evolutionary methods require an initial population. The arguments to this method are the lower and upper bounds of the hyper-box defining the search domain.
1:
randompoint(a, b) = a + (b - a) .* rand(length(a))statusoutputduring the evolution of a population, we may wish to monitor the performance. This function outputs periodically the number of function evaluations and the current most fit solution (see above). The frequency of output decreases with the increase in magnitude of the number of function evaluations performed.
1:
function statusoutput(2:output, # true/false3:nf, # number of function evaluations4:best, # population of Points5:lastmag, # magnitude of last output6:lastnf # nf at last output7:)8:if output9:z = best.z10:if length(z) == 111:z = z[1]12:end13:δ = nf - lastnf14:mag = floor(log10(nf))15:if mag > lastmag16:println("evolution: $nf $z $(best.g)")17:lastmag = mag18:lastnf = nf19:elseif δ > 10^(mag)-120:println("evolution: $nf $z $(best.g)")21:lastnf = nf22:end23:end24:(lastmag, lastnf)25:end
2.2.2. A point in the search domain
We define a Point type to provide a generic interface for the handling of members of a population. The structure includes the actual representation of the solution (i.e. the point in the search domain), the objective function values for the point, and the measure of feasibility. It is assumed in all the implementations of the solvers that the existence of a Point means that the objective function has been evaluated for that point in the search space, reducing the amount of unnecessary computation.
1:struct Point2:x :: Any # decision point3:z :: Vector # objective function values4:g :: Real # constraint violation5:function Point(x, f, parameters = nothing)6:# evaluate the objective function,7:# using parameters if given8:if parameters isa Nothing9:z, g = f(x)10:else11:z, g = f(x, parameters)12:end13:# check types of returned values14:# and convert if necessary15:if g isa Int16:g = float(g)17:end18:if rank(z) == 119:# vector of objective function values20:new(x, z, g)21:elseif rank(z) == 022:# if scalar, create size 1 vector23:new(x, [z], g)24:else25:error( "NatureInspiredOptimization" *26:" methods can only handle scalar" *27:" and vector criteria," *28:" not $(typeof(z))." )29:end30:end31:end
The type is a structure with the three values and a function known as the constructor. The constructor function, in this case, takes the point x, the objective function f, and the optional parameters and evaluates the objective function at that point. The resulting objective function values and the measure of feasibility are saved along with the point.
The constructor uses the rank function, defined here:
1: rank(x :: Any) = length(size(x))
This function is used to check for scalar versus vector values returned by the objective function. We ensure that the objective function values stored are always a vector. This will make handling the results easier and more generic.
In the evolutionary methods implemented below, I will wish to compare different points in the search domain. This function builds on the comparison operators defined above to allow us to compare Point objects:
1: ≻(a :: Point, b :: Point) = (a.g ≤ 0) ? (b.g > 0.0 || a.z ≻ b.z) : (a.g < b.g)
which says that point a is better than point b if a is feasible but b is not, both points are feasible and the objective function values for a are better than for b, or both are infeasible but a has a lower measure of infeasibility.
This function uses the ternary operator ? which is an in-line if-then-else statement.
2.2.3. Fitness calculations
For single objective functions, the fitness of solutions will be a normalised value, \(\phi \in [0,1]\), with a fitness of 1 being the most fit and 0 the least fit. In practice, we will limit the fitness to be \(\phi \in (0,1)\) to avoid edge cases with the boundaries for, at least the PPA, which uses the fitness value directly in identifying new solutions.
The fitness calculations depend on the number of objectives. For single objective problems, the fitness is the objective function values normalised and reversed. The best solution will have a fitness value close to 1 and the worst solution a fitness value close to 0. For multi-criteria problems, a Hadamard product of individual criteria rankings is used to create a fitness value [Fraga and Amusat 2016] with the same properties: more fit, i.e. better, solutions have fitness values closer to 1 than less fit, or worse, solutions.
The fitness calculations also take the feasibility of the points into account. If both feasible and infeasible solutions are present in a population, the upper half of the fitness range, \([0.5,1)\), is used for the feasible solutions and the bottom half, \((0,0.5]\), for the infeasible solutions. If only feasible or infeasible solutions are present, the full range of values is used for whichever case it may be. This simultaneous consideration of feasible and infeasible solutions in a population is motivated by the sorting algorithm used in NSGA-II [Deb 2000].
This function uses a helper function, defined below, to assign a fitness to a vector of objective function values.
1:function fitness(pop :: Vector{Point})2:l = length(pop)3:# feasible solutions are those with g ≤ 04:indexfeasible = (1:l)[map(p->p.g,pop) .<= 0]5:# infeasible have g > 06:indexinfeasible = (1:l)[map(p->p.g,pop) .> 0]7:fit = zeros(l)8:# the factor will be used to squeeze the9:# fitness values returned by vectorfitness into10:# the top half of the interval (0,1) for11:# feasible solutions and the bottom half for12:# infeasible, if both types of solutions are13:# present. Otherwise, the full interval is14:# used.15:factor = 116:if length(indexfeasible) > 017:# consider only feasible subset of pop18:feasible = view(pop,indexfeasible)19:# use objective function value(s) for ranking20:feasiblefit = vectorfitness(map(p->p.z,feasible))21:if length(indexinfeasible) > 022:# upper half of fitness interval23:feasiblefit = feasiblefit./2 .+ 0.524:# have both feasible & infeasible25:factor = 226:end27:fit[indexfeasible] = (feasiblefit.+factor.-1)./factor28:end29:if length(indexinfeasible) > 030:# squeeze infeasible fitness values into31:# (0,0.5) or (0,1) depending on factor,32:# i.e. whether there are any feasible33:# solutions as well or not34:infeasible = view(pop,indexinfeasible)35:# use constraint violation for ranking as36:# objective function values although it37:# should be noted that the measure of38:# infeasibility may not actually make any39:# sense given that points are infeasible40:fit[indexinfeasible] = vectorfitness(map(p->p.g, infeasible)) / factor;41:end42:fit43:end
This code illustrates the use of some functional programming aspects of Julia. In lines 4 and 6, the map function is used to look at the value of g for each member of the population. The comparison within [] generates a vector of true or false values and this vector is used to select the indices from the full set, \(\{1, \ldots, l\}\), where \(l\) is the length of the vector of points.1 On line 18, this vector of indices for the feasible points (if any) is used to create a view into the original population vector consisting purely of the feasible points. Then, on line 20, the map function is used again to look at the objective function values and a fitness value is assigned using the helper function vectorfitness, below. Finally, on line 27, the indices for the feasible points are used to record the fitness values in the vector that will be returned by the fitness function.
The following helper function works with a single vector of objective function values, each of which may consist of single or multiple objectives. For single objective problems, the fitness is simply the normalised objective function value. For multi-objective cases, the fitness is based on the Hadamard product of the rank of each member of population according to each criterion [Fraga and Amusat 2016]. This function uses yet another helper function, adjustfitness, which restricts the fitness values to \((0,1)\).
1:function vectorfitness(v)2:# determine number of objectives (or3:# pseudo-objectives) to consider in ranking4:l = length(v)5:if l == 16:# no point in doing much as there is only7:# one solution8:[0.5]9:else10:m = length(v[1]) # number of objectives11:if m == 1 # single objective12:fitness = [v[i][1] for i=1:l]13:else # multi-objective14:# rank of each solution for each15:# objective function16:rank = ones(m,l);17:for i=1:m18:rank[i,sortperm([v[j][i] for j=1:l])] = 1:l19:end20:# hadamard product of ranks21:fitness = map(x->prod(x), rank[:,i] for i=1:l)22:end23:# normalise (1=best, 0=worst) while24:# avoiding extreme 0,1 values using the25:# hyperbolic tangent26:adjustfitness(fitness)27:end28:end
Line 18 ranks each solution according to each individual objective function: the values for the solutions for a given objective function are sorted using sortperm and the rank assigned as a value between 1 and the number of solutions. Then, on line 21, the different rankings are combined into a single fitness value for each solution using the Hadamard product.
The fitness should be a value ∈ (0,1), i.e. not including the bounds themselves as those values may cause edge effects when the fitness value is used directly to define new points in the search domain. Therefore, we adjust the fitness values to ensure that the bounds are not included. The side effect of this adjustment, using the tanh function [Salhi and Fraga 2011], is that the fitness is given a sigmoidal shape, steepening the curve around the middle range of fitness values. This potentially affects those methods that use the actual fitness value for the generation of new points in the search space [Vrielink and van den Berg 2021b; Vrielink and van den Berg 2021a] but does not affect the relative ranking of points in the population.
1:function adjustfitness(fitness)2:if (maximum(fitness)-minimum(fitness)) > eps()3:0.5*(tanh.(4*(maximum(fitness) .- fitness) /4:(maximum(fitness)-minimum(fitness)) .- 2)5:.+ 1)6:else7:# if there is only one solution in the8:# population or if all the solutions are9:# the same, the fitness value is halfway10:# in the range allowed11:0.5 * ones(length(fitness))12:end13:end
2.2.3.1. Test the fitness method
Later, I will present a case study involving the design a process for purification of chlorobenzene (Chapter 3). This case study has two criteria for assessing the design: the capital cost and the operating cost. Therefore, the fitness has to consider both objectives. Consider a population consisting of process designs at some particular point, x0, at the lower bounds on all variables, at the upper bounds, and at a point midway between the bounds. This code snippet evaluates the fitness at these four points:
1:using NatureInspiredOptimization: Point, fitness2:using NatureInspiredOptimization.Chlorobenzene: process, evaluate3:flowsheet, x0, lower, upper, nf = process()4:population = [5:Point(x0, evaluate, flowsheet)6:Point(lower, evaluate, flowsheet)7:Point(upper, evaluate, flowsheet)8:Point(lower + (upper-lower)/2.0, evaluate, flowsheet)9:]10:fitness(population)
The results of the bi-criteria fitness calculation using the Hadamard product are:
| 0.807216925065357 |
| 0.9820137900379085 |
| 0.01798620996209155 |
| 0.4822791408831034 |
The fitness values have been calculated based solely on the measure of infeasibility because all the solutions are infeasible. If the solutions considered were to include a feasible point, the results will differ. From a previous study of the chlorobenzene process, a known feasible solution can be evaluated:
1:using NatureInspiredOptimization.Chlorobenzene: process, evaluate2:flowsheet, x0, lower, upper, nf = process()3:4:evaluate([1.3303962289290255:0.86574560560833786:17:1.2173537128058718:0.99524655243847779:1.2523035637552410:1.44859348748093611:0.96955390109404212:2.080117425247644], flowsheet)
and which has objective function values
([2.15517966714251e6, 1.7474586736116146e6], 0.0)
with a 0.0 value for the constraint violation, indicating that this solution is indeed feasible. If we now evaluate a population that includes this solution as well,
1:using NatureInspiredOptimization: Point, fitness2:using NatureInspiredOptimization.Chlorobenzene: process, evaluate3:flowsheet, x0, lower, upper, nf = process()4:population = [5:Point(x0, evaluate, flowsheet)6:Point(lower, evaluate, flowsheet)7:Point(upper, evaluate, flowsheet)8:Point(lower + (upper-lower)/2.0, evaluate, flowsheet)9:Point([1.33039622892902510:0.865745605608337811:112:1.21735371280587113:0.995246552438477714:1.2523035637552415:1.44859348748093616:0.96955390109404217:2.080117425247644], evaluate, flowsheet)18:]19:fitness(population)
the fitness values are:
| 0.4036084625326785 |
| 0.4910068950189542 |
| 0.008993104981045774 |
| 0.2411395704415517 |
| 0.875 |
All the infeasible solutions have been assigned fitness values in the lower half of the range, \((0,0.5)\), and the single feasible solution has been given a fitness value in the top half of the range. Although the fitness values of the infeasible solutions differ from the previous example, their relative ranking remains the same within the set of infeasible members.
2.2.4. Selecting points based on fitness
Nature inspired optimization methods often require selecting one or more members of a population, such as for creating new solutions for the next generation based on current solutions. This selection will typically be based on the fitness: the more fit a solution is, the more likely it is to be selected. There are many methods available for selection including, for instance, the best in the population, a roulette wheel analogue, and tournament selection [Goh et al. 2003]. In this book, we will be using the tournament selection, with a tournament size of 2 as we have found this to be a good choice for problems in process systems engineering.
The function implemented below returns the index into the population for the selected point. The argument is the vector of fitness values, φ.
1:function select(ϕ)2:n = length(ϕ)3:@assert n > 0 "Population is empty"4:if n ≤ 15:16:else7:i = rand(1:n)8:j = rand(1:n)9:ϕ[i] > ϕ[j] ? i : j10:end11:end
Note the use of @assert to catch a situation that should not happen: attempting to select from an empty population. @assert expects a condition and an optional error message to output if the condition is not satisfied.
2.2.5. Quantifying the quality of multi-objective solutions
The fitness calculations, above, section 2.2.3, are suitable for multi-objective optimization problems because they incorporate all the objectives in the calculation of the fitness. However, we need to be able to quantify a measure of the quality of the population obtained by each method if we wish to compare the performance of different methods. For single objective problems, the objective function value of the best solution in the final population gives us that measure. For multicriteria problems, no such single value is present in the population of points returned by any method.
The equivalent of best for a multicriteria problem is the set of non-dominated points (see Section 2.2.1 for the definition and implementation). The best outcome obtained is the approximation to the Pareto frontier. This approximation is the set of all the points in the final population that are not dominated. Ideally, a measure of the quality of the set of non-dominated points returned by a method will be based on how close the set is to this frontier and how well the frontier is represented in terms of breadth [Riquelme et al. 2015]. However, as the actual frontier is not known, any quantification will need to be relative, which may allow us to say whether one method is better than another for an individual case study or what combination of parameter values for a given method leads to the best outcomes.
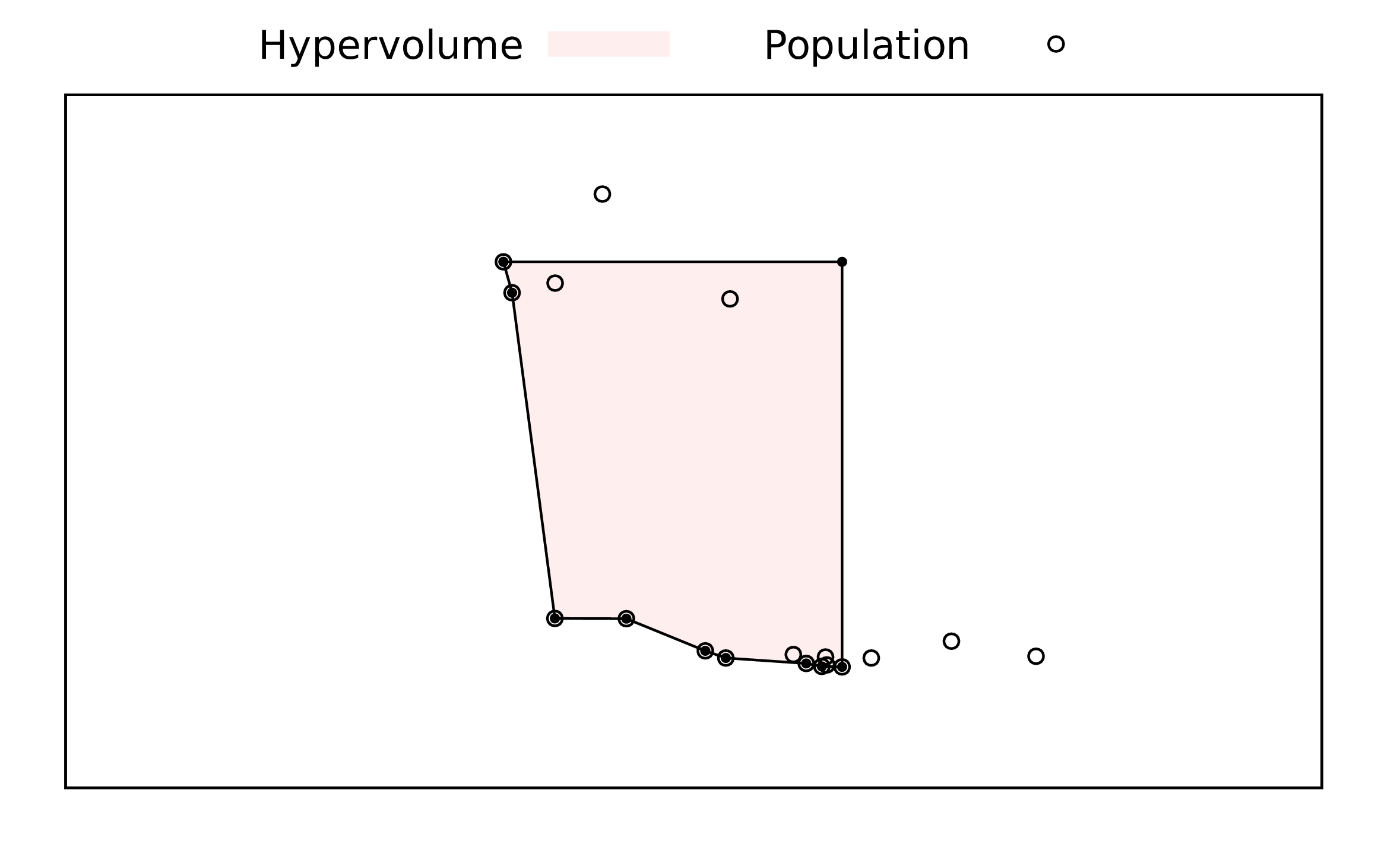
Figure 1: An illustration of the hyper-volume (area for bicriteria case) used as a measure of the quality of the solutions obtained. The circles are points in the population, plotted in objective function space with each axis corresponding to one criterion and with the assumption that each criterion is a value to be minimised. Those open circles that include a filled circle are non-dominated points, a set that is meant to be an approximation to the Pareto frontier. The shaded area is the hyper-volume to be calculated.
The method suggested in this book is an estimate of the hyper-volume described by a convex region defined by the set of non-dominated points and the extensions of the best points for each criterion. Figure 1 illustrates the hyper-volume for a bi-criteria problem, with the area measured shaded.
The hypervolume gives an indication of the breadth of the approximation to the Pareto frontier but it does not assess the quality of the approximation with respect to the actual frontier. To compare between methods, we also incorporate the distance to a utopia point. As this point is not known, we use a point that is in the right direction. For minimisation problems where the objective function values are all positive real values, we can use the origin as the utopia point.
The ratio of the hyper-volume to the distance to the utopia point, squared, is a measure that can be used to compare different methods. It captures the aspects that are of concern; whether the actual measure has any meaning is unclear.
The following code implements the calculation of the hypervolume, actually an area, and distance to the utopia point for bicriteria problems. The argument to the function is the set of non-dominated points in the population.
1:function hypervolume(points)2:m = length(points)3:n = length(points[1].z)4:set = Matrix{Real}(undef, m, n)5:for r ∈ 1:m6:set[r,1:n] = points[r].z7:end8:z = sortslices(set, dims=1, by=x->(x[1], x[2]))9:area = 0.010:last = z[m,n]11:first = z[1,1]12:distance = sqrt(z[1,1]^2 + z[1,2]^2)13:for i ∈ 2:m14:area += (z[i,1]-z[i-1,1]) * ((z[1,2]-z[i-1,2])+(z[1,2]-z[i,2])) / 2.015:d = sqrt(z[i,1]^2 + z[i,2]^2)16:if d < distance17:distance = d18:end19:end20:# maximise area, minimise distance21:# larger outcome better22:area/distance^223:end
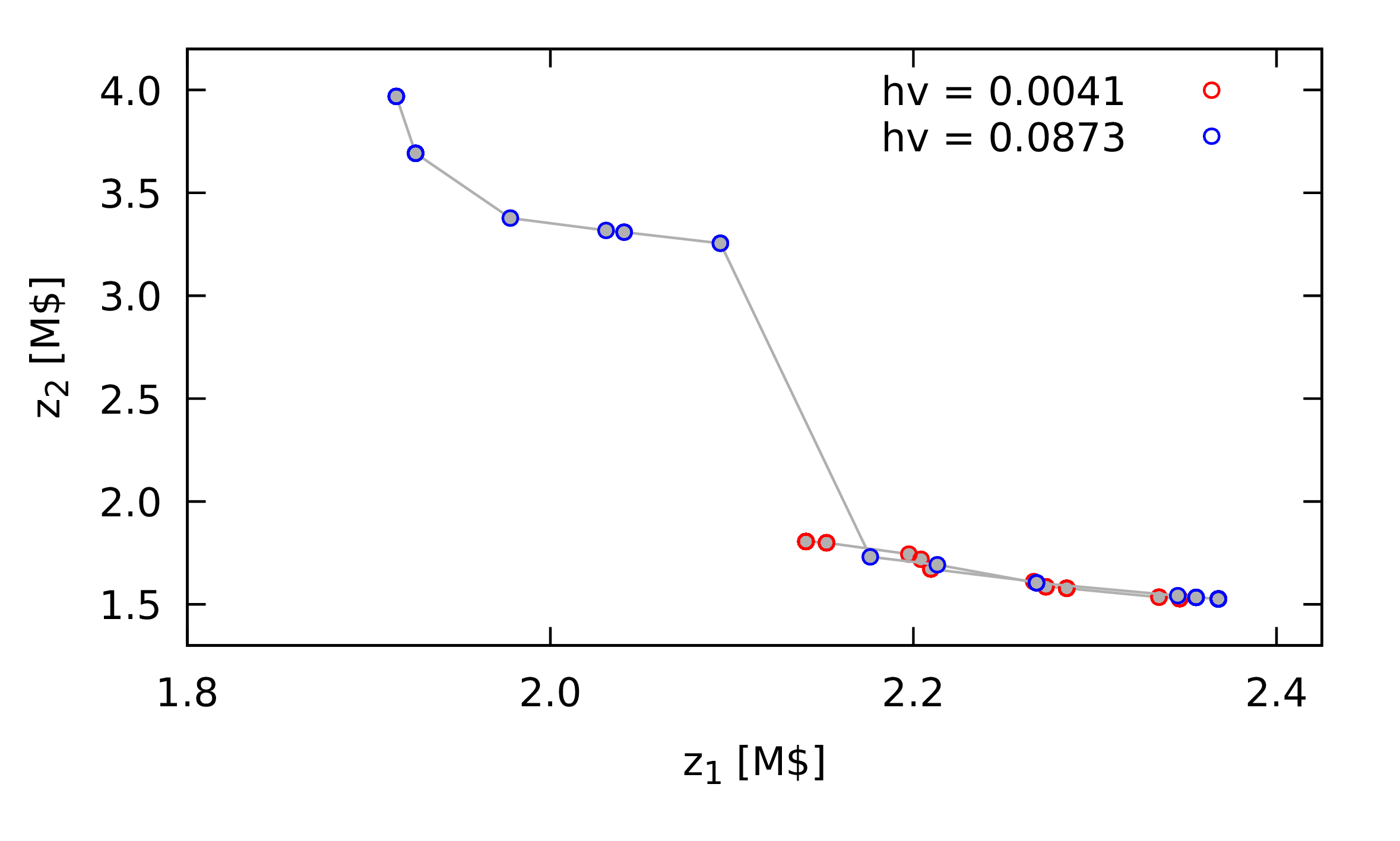
Figure 2: Comparison of set of non-dominated points obtained using a nature inspired method with different outcomes, illustrating the difference between an outcome with a low hypervolume measure (\(hv = 0.0041\), in red) and an outcome with a higher hypervolume measure (\(hv = 0.0873\), in blue). \(z_1\) and \(z_2\) are the two objective function values, with the goal of minimising both.
Later, I will present the application of nature inspired methods for a chemical process design problem. Figure 1 shows two different outcomes from such a method. In red, bottom right of the plot, is the less desirable outcome, as compared with the outcome in blue which has greater breadth and similar quality in terms of actual any single combination of objective function values obtained.
2.3. Genetic Algorithms
Genetic algorithms are inspired by Darwinian evolution and, specifically, the survival of the fittest together genetic operators based on sexual reproduction and mutations [Holland 1975; Goldberg 1989; Goh et al. 2003; Katoch et al. 2021]. There are three key aspects that define a genetic algorithm:
- selection, based on fitness;
- crossover where new solutions are generated inspired by meiosis; and,
- mutation where a new solution is generated by a small modification to an existing solution.
The basic algorithm is shown in Algorithm 2.
As presented, the algorithm does not include elitism. Elitism is a means of ensuring that a very good solution identified during the evolutionary procedure is not lost due to selection. In the implementation below, the best solution in any generation will automatically be included in the next population. This is known as elitism of size 1. For multi-objective optimization problems, the best solution will be one chosen arbitrarily from the set of non-dominated solutions, typically the solution that is the best with respect to one of the criteria. Other forms of elitism, especially for multi-objective problems, are possible and often desirable.

There are many variations on this algorithm, such as whether mutation should be applied potentially to the new solutions obtained by crossover and whether there should be a form of elitism where the best solutions in a population are guaranteed to be in the new population. Neither of those aspects are included in this algorithm. The aim of this book is not to explore the impact of the many variations possible but to illustrate the commonalities and differences between different nature inspired evolutionary population based methods.
The stopping criterion for this method, as for the others presented in the next chapters, will be the number of function evaluations. Again, many different stopping criteria could be considered including the number of cycles or generations to perform, the total time elapsed, and whether the population is stable in the sense that there is no longer any improvement in the best solution or solutions. As one of the case studies has significant computational requirements, the chlorobenzene process design, the number of function evaluations is an appropriate stopping criterion. Although it does not take into account the overhead of the actual method, the three methods considered in this book will have similar overhead.
From the algorithm, the outcome will be based on the implementation of the select, crossover, and mutate functions as well as the values of the parameters: the population size, \(n_p\), the crossover rate, \(r_c\), and the mutation rate, \(r_m\). These functions and parameters will typically require adaptation to the particular problem. The select method, however, will be generic and has already been defined above in Section 2.2.4. The crossover and mutate methods need to be based on the specific representation of solutions so may need tailored implementations.
2.3.1. The crossover operation
Many problems are based on vectors of real numbered values for the decision variables. An example is the chlorobenzene process design problem already alluded to. Therefore, it makes sense to have a function for crossover that works on such representations. Again, multiple dispatch will ensure the appropriate implementation is chosen depending on the data types used to represent decision points.
Crossover may be single point, where all elements before that point are swapped, it may be two points, or it could in fact be considered value by value in the representation vector. We implement the latter in this book as, arguably, it is more general and does not impose any meaning into the order of the decision variables in the chromosome. A multi-point crossover subsumes both single and two point crossover methods.
1:function crossover(p1 :: Vector{T}, p2 :: Vector{T}) where T <: Number2:n = length(p1)3:@assert n == length(p2) "Points to crossover must be of same length"4:# generate vector of true/false values with5:# true meaning "selected" in comments that6:# follow7:alleles = rand(Bool, n)8:# first new solution (n1) consists of p1 with9:# selected alleles from p2; note that we need10:# to copy the arguments as otherwise we would11:# be modifying the contents of the arguments.12:n1 = copy(p1)13:n1[alleles] = p2[alleles]14:# the second new solution is the other way15:# around: p2 with selected from p116:n2 = copy(p2)17:n2[alleles] = p1[alleles]18:n1, n219:end
Note that we fully qualify the arguments to the function by data type. This will enable Julia to apply the appropriate crossover implementation depending on the data type for the representation used for points in the search space. Later we shall see how we implement a different crossover function for the TSP representation, a Path.
To test out this code, we create two vectors of real numbers and apply the crossover several times to these to see how the results vary:
1:using NatureInspiredOptimization: printvector2:using NatureInspiredOptimization.GA: crossover3:using Printf4:let x1 = rand(4), x2 = rand(4)5:@printf "\n "6:printvector("x1: ", x1)7:@printf "| "8:printvector("x2: ", x2)9:@printf "\n\n"10:for i ∈ 1:511:@printf "%d. " i12:n1, n2 = crossover(x1,x2)13:printvector("n1: ", n1)14:@printf "| "15:printvector("n2: ", n2)16:@printf "\n"17:end18:end
which generates output such as this:
x1: 0.210 0.587 0.845 0.819 | x2: 0.657 0.392 0.471 0.275 1. n1: 0.657 0.392 0.471 0.275 | n2: 0.210 0.587 0.845 0.819 2. n1: 0.657 0.587 0.845 0.819 | n2: 0.210 0.392 0.471 0.275 3. n1: 0.657 0.587 0.845 0.819 | n2: 0.210 0.392 0.471 0.275 4. n1: 0.657 0.587 0.471 0.819 | n2: 0.210 0.392 0.845 0.275 5. n1: 0.210 0.587 0.845 0.275 | n2: 0.657 0.392 0.471 0.819
2.3.2. The mutation operator
Mutation introduces new genetic material into the population by creating new solutions based on existing ones with a small change. In a bit-wise representation, a small change would be toggling one of the bits. For a real number vector representation, a small change has been defined by a random change to one element of the vector. The following code implements this, ensuring that the changed element remains within the bounds defined for the decision variables:
1:function mutate(p, lower, upper)2:m = copy(p) # passed by reference3:n = length(p) # vector length4:i = rand(1:n) # index for value to mutate5:a = lower[i] # lower bound for that value6:b = upper[i] # and upper bound7:r = rand() # r ∈ [0,1]8:# want r ∈ [-0.5,0.5] to mutate around p[i]9:m[i] = p[i] + (b-a) * (r-0.5)10:# check for boundary violations and rein back in11:m[i] = m[i] < a ? a : (m[i] > b ? b : m[i])12:m13:end
Of special note is line 2 where a copy of the specific point is made. Julia passes vectors, for instance, by reference so any modification of the argument will affect the variable in the calling function. In this case, we want to create a new point in the search space without changing the existing point. Therefore, we make a copy of the argument before modifying it.
Again, we can test out the mutation operator by creating an initial vector and applying the operator several times:
1:using NatureInspiredOptimization: printvector2:using NatureInspiredOptimization.GA: mutate3:using Printf4:let x = rand(5);5:@printf "\n "6:printvector("x: ", x)7:@printf "\n\n"8:for i ∈ 1:59:@printf "%d. " i10:n = mutate(x,11:zeros(length(x)),12:ones(length(x)))13:printvector("n: ", n)14:@printf "\n"15:end16:end
which generates output such as this:
x: 0.166 0.154 0.703 0.909 0.348 1. n: 0.626 0.154 0.703 0.909 0.348 2. n: 0.166 0.154 0.703 0.909 0.315 3. n: 0.166 0.154 0.703 0.909 0.729 4. n: 0.166 0.154 0.703 1.000 0.348 5. n: 0.166 0.154 0.730 0.909 0.348
2.3.3. The implementation
With the three key operations (select, crossover, mutate) defined, the genetic algorithm itself can be implemented:
1:using NatureInspiredOptimization: fitness, mostfit, Point, select, statusoutput2:function ga(3:# required arguments, in order4:p0, # initial population5:f; # objective function6:# optional arguments, in any order7:lower = nothing, # bounds for search domain8:upper = nothing, # bounds for search domain9:parameters = nothing, # for objective function10:nfmax = 10000, # max number of evaluations11:np = 100, # population size12:output = true, # output during evolution13:rc = 0.7, # crossover rate14:rm = 0.05) # mutation rate15:16:p = p0 # starting population17:lastmag = 0 # for status output18:lastnf = 0 # also for status output19:nf = 0 # count evaluations20:while nf < nfmax21:ϕ = fitness(p)22:best = mostfit(p,ϕ)23:newp = [best] # elite size 124:lastmag, lastnf = statusoutput(output, nf,25:best, lastmag,26:lastnf)27:i = 028:while i < np29:print(stderr, "nf=$nf i=$i\r")30:point1 = p[select(ϕ)]31:if rand() < rc # crossover?32:point2 = p[select(ϕ)]33:newpoint1, newpoint2 = crossover(point1.x, point2.x)34:push!(newp,35:Point(newpoint1, f, parameters))36:push!(newp,37:Point(newpoint2, f, parameters))38:nf += 239:i += 240:elseif rand() < rm # mutate?41:newpoint1 = mutate(point1.x, lower, upper)42:push!(newp,43:Point(newpoint1, f, parameters))44:nf += 145:i += 146:else # copy over47:push!(newp, point1)48:i += 149:end50:end51:p = newp52:end53:ϕ = fitness(p)54:best = mostfit(p,ϕ)55:lastmag, lastnf = statusoutput(output, nf,56:best,57:lastmag, lastnf)58:best, p, ϕ59:end
Given that this is the first full optimization method implemented in the book, it is worth describing many of the lines of code, by line number:
- This brings in the named functions and types from the main module, including the
fitnessandselectfunctions. - There are two required arguments for the
gamethod: the initial population,p0, and the objective function used to evaluate points in the search space. - This argument and the ones that follow are optional. We will see below how optional arguments are specified when the function is invoked. The values given here are the defaults for when the arguments are not specified.
- All the methods will use the same stopping criterion: a maximum number of evaluations of the objective function. So
nfkeeps count of how many evaluations have been invoked andnfmaxis the limit. - The genetic algorithm will be specified with a rate for crossover and a rate for mutation. On this line, a decision is made to cross the solution obtained, on the previous line, with another solution. Line 40 similarly checks to see if the selected solution should be mutated. If neither condition holds, line 46, the point selected is simply inserted in the new population,
newp. - For crossover, two solutions are required so a second solution is selected. The following lines apply the crossover function and add the resulting points to the population.
- For mutation, the already selected point is evaluated and added to the population.
- The GA function returns the best solution in the final population, the full population itself, and the fitness of that population. The latter two elements are useful for gaining insight into the performance of the evolution (e.g. diversity) and for debugging should it be necessary.
The implementation is based on some implicit decisions as well. For instance, many authors of genetic algorithms will apply the mutation operator potentially to each of the solutions obtained by the crossover operation. I have taken decision to not do this, noting that any solution that results from crossover will have a chance to be selected for mutating in the next generation. Note also that this implementation does not make use of the inherent parallelism: all the new points could be collected and evaluated in parallel at the end of each generation. The implementation for the plant propagation algorithm (Chapter 2.5 below) will do this, however. The aim of this book is not to achieve the most efficient implementations but to illustrate what is possible in Julia. Comparisons presented later will focus on the quality of the solutions obtained and not the computational performance.
2.4. Particle Swarm Optimization
The original method was developed by Kennedy & Eberhart [Kennedy and Eberhart 1995]. The basic idea is that each particle (a solution to the optimization problem) in a swarm has a velocity, allowing it to move through the search space. This velocity is adjusted each iteration by taking into account each particle's own history, specifically the best point it has encountered to date, and the swarm's overall history, the best point encountered by all particles in the swarm. See Algorithm 1.

The equation for updating the velocity of each particle, \(i\), is
\begin{equation} \label{org2663845} v_i \gets \omega v_i + c_1 \left ( h_i - x_i \right ) + c_2 \left ( b - x_i \right ) \end{equation}where \(x_i\) is the current position of the particle, \(v_i\) its velocity, \(h_i\) the best place this particle has been (its historical best), and \(b\) the best point found by the whole population so far. The ω parameter provides inertia for non-zero values and the parameters \(c_1\) and \(c_2\) weigh the contributions from local history and global history towards the change in velocity.
Due to the calculations for updates to velocities and the use of the velocities to move the particles, this method is naturally directed at problems where the decision variables are real numbers. Although the method has been adapted to integer problems [Datta and Figueira 2011], the implementation here is for real-valued vectors as decision variables.
2.4.1. The implementation
The implementation has a similar layout to that for the genetic algorithm, consisting of a loop where the population of solutions is updated. It is simpler in that every member of the population is updated using the velocities and these velocities are updated continually by equation \eqref{org2663845}.
1:using NatureInspiredOptimization: ≻, Point, randompoint, statusoutput2:function pso(3:# required arguments, in order4:p0, # initial population5:f; # objective function6:# optional arguments, in any order7:lower = nothing, # bounds for search domain8:upper = nothing, # bounds for search domain9:parameters = nothing, # for objective function10:nfmax = 10000, # max number of evaluations11:np = 10, # population size12:output = true, # output during evolution13:c₁ = 2.0, # weight for velocity14:c₂ = 2.0, # ditto15:ω = 1.0 # inertia for velocity16:)17:18:# create initial full population including p019:p = copy(p0)20:for i ∈ length(p0)+1:np21:push!(p, Point(randompoint(lower, upper),22:f, parameters))23:end24:nf = np25:# find current best in population26:best = begin27:b = p[1]28:for i ∈ 2:np29:if p[i] ≻ b30:b = p[i]31:end32:end33:b34:end35:h = p # historical best36:v = [] # initial random velocity37:for i ∈ 1:np38:push!(v, (upper .- lower) .*39:( 2 * rand(length(best.x)) .- 1))40:end41:lastmag = 0 # for status output42:lastnf = 0 # as well43:while nf < nfmax44:lastmag, lastnf = statusoutput(output, nf,45:best,46:lastmag,47:lastnf)48:for i ∈ 1:np49:print(stderr, "nf=$nf i=$i\r")50:v[i] = ω * v[i] .+51:c₁ * rand() * (h[i].x .- p[i].x) .+52:c₂ * rand() * (best.x .- p[i].x)53:x = p[i].x .+ v[i]54:# fix any bounds violations55:x[x .< lower] = lower[x .< lower]56:x[x .> upper] = upper[x .> upper]57:# evaluate and save new position58:p[i] = Point(x, f, parameters)59:nf += 160:# update history for this point61:if p[i] ≻ h[i]62:h[i] = p[i]63:end64:# and global best found so far65:if p[i] ≻ best66:best = p[i]67:end68:end69:end70:lastmag, lastnf = statusoutput(output, nf, best,71:lastmag, lastnf)72:best, p73:end
Some notes, again by line number:
- The default values of the velocity update parameters are based on the analysis presented below in the first substantial case study and are in line with the original implementation [Kennedy and Eberhart 1995].
- This loop ensures that the population of points has the desired number of points. The PSO method differs from the others in that each individual in the population evolves but no new points are created. This is a subtle distinction but the implication is that the initial population must have the correct number of solutions.
- The initial velocity of each particle is randomly allocated.
- Velocity updated.
- Point moved according to the velocity with the following lines ensuring all values of the point are within the bounds for the search domain.
- This line and the ones that follow update both the point's own historical best as well as the overall population's best solution to date.
2.5. Plant Propagation Algorithms
The plant propagation algorithm (PPA) [Salhi and Fraga 2011] is inspired by one of the methods used by strawberry plants to propagate: the generation of runners. In fertile soil, strawberry plants send of a number of short runners to exploit the current surroundings. In less fertile soil, fewer yet longer runners propagate to explore more broadly. The PPA therefore creates new solutions, based on existing solutions in a population, by generating a number of runners. The number of runners is proportional to the fitness and the distance these runners propagate is inversely proportional to the fitness. This is similar in motivation as an adaptive scheme for mutation in genetic algorithms [Marsili Libelli and Alba 2000].
The PPA is shown in Algorithm 1.

The plant propagation algorithm depends on three support functions: fitness, select, and neighbour. The first two have already been implemented as generic functions suitable for any method. The last, however, is specific to the plant propagation algorithm.
2.5.1. Identifying neighbouring solutions
Propagation, whether in the close vicinity of an existing solution or further away, is defined through the neighbour function. This function is similar to the mutate function implemented for the genetic algorithm method. It differs in that the random change is a function of the fitness of the solution to propagate.
In the mutate method for the genetic algorithm, for the case of decision variables being represented by a vector of real values, a single value is chosen for change. For the neighbour function, all values are changed simultaneously, each with a different random number. In all cases, the amount to change each variable is adjusted by the fitness: the fitter the solution, the smaller the changes considered; the less fit the solution, the larger the changes allowed.
1:function neighbour(s, # selected point2:lower, # lower bounds3:upper, # upper bounds4:ϕ) # fitness5:r = rand(length(s))6:# element by element calculation7:ν = s + (upper - lower) .*8:((2 * (r .- 0.5)) * (1-ϕ))9:# check for bounds violations10:ν[ν .< lower] = lower[ν .< lower]11:ν[ν .> upper] = upper[ν .> upper]12:return ν13:end
Lines 7 and 8 create a new solution from the current selected solution by using the random numbers from line 5 and adjusting these through the fitness, φ. The new point is adjusted to ensure it remains within the bounds of the search domain in lines 10 and 11.
2.5.2. The implementation
With the neighbour function implemented, the full plant propagation algorithm can be written:
1:using NatureInspiredOptimization: fitness, mostfit, Point, select, statusoutput2:function ppa(3:# required arguments, in order4:p0, # initial population5:f; # objective function6:# optional arguments, in any order7:lower = nothing, # bounds for search domain8:upper = nothing, # bounds for search domain9:parameters = nothing, # for objective function10:nfmax = 10000, # max number of evaluations11:np = 10, # population size12:output = true, # output during evolution13:nrmax = 5) # maximum number of runners14:15:p = p0 # starting population16:lastmag = 0 # for status output17:lastnf = 0 # also for status output18:nf = 0 # function evaluations19:while nf < nfmax20:ϕ = fitness(p)21:best = mostfit(p,ϕ)22:newp = [best] # elite set size 123:lastmag, lastnf = statusoutput(output, nf,24:best,25:lastmag,26:lastnf)27:newpoints = []28:for i ∈ 1:np29:print(stderr, "nf=$nf i=$i\r")30:s = select(ϕ)31:nr = ceil(rand() * ϕ[s] * nrmax)32:for j ∈ 1:nr33:push!(newpoints,34:neighbour(p[s].x, lower,35:upper, ϕ[s]))36:nf += 137:end38:end39:Threads.@threads for x in newpoints40:push!(newp, Point(x, f, parameters))41:end42:p = newp43:end44:ϕ = fitness(p)45:best = mostfit(p,ϕ)46:lastmag, lastnf = statusoutput(output, nf,47:best,48:lastmag, lastnf)49:best, p, ϕ50:end
Again, this implementation has a similar layout as the previous two methods. The key differences are the following lines:
- The number of runners, i.e. new solutions to generate from an existing solution, is a random number up to \(n_{r,\max}\) adjusted by the fitness, \(\phi_s\). Recall that the fitness value is ∈ (0,1). The fitter the solution, the more runners are likely.
- The runners are created using the
neighbourfunction and stored in thenewpointsvector. The points are not evaluated here; the evaluation is postponed until line 38. All the points created in this overall loop are evaluated now, potentially in parallel through the use of Julia's
@threadsmacro. By default, only a single thread is available but Julia can be told to use multiple threads. See Section 1.5.3.
2.6. Random search
It is useful to have a control experiment to confirm that any or all of the above methods are indeed effective at search. Whether a fully random search could be considered a method inspired by nature or not, such a method is in the spirit of the other nature inspired methods in being stochastic. There are no parameters and the method relies on a function to generate new random solutions in the search space.
The actual search generates \(n_f\) random points, and to provide some statistics for comparison with the evolutionary methods, output is generated periodically with the best solution found so far.
1:using NatureInspiredOptimization: Point, statusoutput2:function randomsearch(3:# required arguments, in order4:f; # objective function5:# optional arguments, in any order6:lower = nothing, # bounds for search domain7:upper = nothing, # bounds for search domain8:parameters = nothing, # for objective function9:nfmax = 10000, # max number of evaluations10:output = true) # output during evolution11:12:lastmag = 0 # for status output13:lastnf = 0 # also for status output14:15:best = Point(randompoint(lower,upper), f,16:parameters)17:nf = 1 # function evaluations18:while nf < nfmax19:p = Point(randompoint(lower,upper),20:f, parameters)21:nf += 122:if p ≻ best23:best = p24:end25:lastmag, lastnf = statusoutput(output, nf,26:best,27:lastmag,28:lastnf)29:end30:lastmag, lastnf = statusoutput(output, nf,31:best,32:lastmag, lastnf)33:best34:end
2.7. Illustrative example
A simple benchmark problem is now present to illustrate how the nature inspired methods may be used. The benchmark problem is
\begin{align} \label{orga2aeda6} \min_x f(x) &= \sum_{i=1}^{d}\left( \sum_{j=1}^d \left (j^i - \beta \right) \left ( \left ( \frac {x_j} {j} \right )^i -1 \right ) \right )^2 \\ x & \in [-d, d]^d \subset \mathbb{R}^d \nonumber \end{align}where \(d\) is dimension of \(x\) and β typically 0.5. This is a continuous function defined on the full domain. It is smooth. As such, it is not the type of problem that requires black box optimization methods. However, this benchmark problem has been chosen to demonstrate the Julia code required to define a problem and solve it using the different solvers described previously.
The first step is to define a function that implements the objective function in Equation \eqref{orga2aeda6}:
1:function permdbeta(x, β = 0.5)2:d = length(x)3:z = sum( sum( (j^i + β)*((x[j]/j)^i - 1) for j ∈ 1:d )^2 for i ∈ 1:d )4:(z, 0)5:end
This code illustrates some elegant programming elements of Julia for working with vectors. The summation signs in Eq. \eqref{orga2aeda6} translate directly into Julia: line 3. For instance, \(\sum_{i=1}^n x_i\) may be written as
sum( x[i] for i in 1:n )
in Julia.
The first line illustrates the use of default values for positional arguments, as opposed to optional arguments, when those arguments are not specified when the function is invoked. In this case, if only one argument is given, i.e. x, the value of β defaults to 0.5. This is the value typically used as a benchmark.
The code also highlights, line 4, that the objective function must return a tuple consisting of the actual value of the objective function, z, along with an indication of constraint satisfaction: 0 or less for a feasible point, a value greater than 0 for infeasible with the actual value ideally a measure of how far from feasible the point may be. For this example, as the problem is feasible over the full domain, the second element of the tuple is always zero.
For all the methods, the following initialization is common:
1:using NatureInspiredOptimization: Point2:d = 4 # dimension3:x0 = zeros(d) # initial guess4:a = -d * ones(d) # domain5:b = d * ones(d) # domain6:p0 = [Point(x0,permdbeta)] # initial population
where the dimension of the problem is set to 4, an initial point at the origin is defined, and the lower and upper bounds of the search domain defined. The initial population, p0, consists of the initial point evaluated with the objective function.
The GA and PSO methods require an initial population that is of the size they expect to evolve. The PPA can start with a population of size 1. However, for consistency, all methods will be started with the same size initial population:
1:using NatureInspiredOptimization: randompoint2:n = 40 # population size3:while length(p0) < n4:push!(p0, Point(randompoint(a, b), permdbeta))5:end
Given the random initial population, we can now apply each of the methods. First, the genetic algorithm:
1:using NatureInspiredOptimization.GA: ga2:gabest, gapop = ga(p0, permdbeta;3:np = n,4:lower = a,5:upper = b,6:nfmax = 10_000_000)
Note that use of _ to denote separation of digits for large numbers, in line 2. 10_000_000 is much easier to read than 10000000 although, of course, we could have used exponential notation, 1e7.
The particle swarm optimization method is invoked similarly:
1:using NatureInspiredOptimization.PSO: pso2:psobest = pso(p0, permdbeta;3:lower = a,4:upper = b,5:np = n,6:nfmax = 10_000_000)
Next, the plant propagation algorithm which differs in that the population size, n, is smaller than that used for the other methods. This is partly because the PPA generates multiple new solutions from each solution chosen for propagation, on average 2.5-3 for each, and also because of the results of the analysis we present in the next section of this book:
1:n = 10 # population size2:using NatureInspiredOptimization.PPA: ppa3:ppabest, ppapop = ppa(p0, permdbeta;4:np = n,5:lower = a,6:upper = b,7:nfmax = 10_000_000)
Finally, as the control for the experiment, the random search method:
1:using NatureInspiredOptimization: randomsearch2:rsbest = randomsearch(permdbeta;3:lower = a,4:upper = b,5:nfmax = 10_000_000)
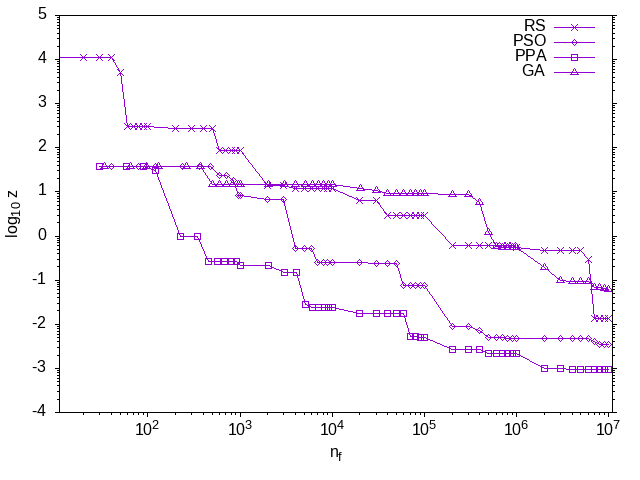
Figure 1: The evolution of the best solution in the current population for each of the three nature inspired optimization methods along with the random search. The profiles for all of the methods, except for the random search, share the starting point as the same initial random population was used. The profiles show that all the methods improve over time. The PPA has the fastest rate of decrease, followed by the PSO and GA methods. The random search is slower initially but actually finds a better solution than the GA by the end. Both axes are plotted in a log scale.
The results from the above code are summarised in Figure 1. This figure shows the evolution of the best solution in the population. The stochastic nature of the methods means that every time one of the methods is applied, the results will differ. When we present a number of case studies below, this stochastic nature will be taken into account by solving each problem multiple times and performing some statistical analysis. For this illustrative example, however, only one attempt has been considered for each method, simply to illustrate how the methods are used and what results may look like. No conclusions about the efficacy of any of the methods should be drawn from this one experiment. The focus of this book is not on benchmark problems such as Equation \eqref{orga2aeda6} but on problems which arise in process systems engineering, as we shall see in the next chapter.
3. Chlorobenzene purification process
The design and optimisation of process flowsheets is a challenging task due to the nonlinear models required and the multi-criteria nature of the objectives for evaluating alternative designs [Biegler et al. 1997; Grossmann and Kravanja 1995]. A process flowsheet consists of a number of processing steps, often referred to as units, with streams connecting the steps. The problem of design is to determine the operating conditions and sizing parameters for the units in the process to achieve desired objectives subject to a number of constraints, both physical (or chemical) and economic.
Process systems engineers often use simulation software to investigate the impact of design parameters, e.g. distillation column size, on their desired objectives. Automating the process requires interfacing optimization methods with simulation software. General modelling languages can be interfaced with Julia: see the OpenModelica interface as an example [Shitahun et al. 2013]. In this case study, the Jacaranda system [Fraga et al. 2000] is used as the simulation tool.
Optimization methods using a simulation system as the model for an optimization problem will need to be able to handle the noise introduced by simulation software due to iterative methods in simulation and convergence tolerances, the possible failure of simulation, and potentially discontinuous objective functions. Nature inspired optimization methods are therefore attractive for this type of optimization problem.
3.1. The process
The case study is the optimisation of a purification section in the production of chlorobenzene. In the overall process, large quantities of benzene are used. Due to the partial conversion in the reaction section of the process, significant quantities of un-reacted benzene would be wasted if not recycled. To recycle the benzene, a stream consisting of primarily benzene needs to be further purified to ensure that the benzene sent back upstream in the process is pure enough to not affect the reaction. The case study we consider here is the design of this purification stage of the overall process.
The stage comprises three distillation units with a feed stream described in Table 1. Although the main aim is to purify the benzene recycle stream, the feed stream to this stage also contains some amount of the main product of the process, chlorobenzene. It is desirable to separate this product as well in sufficiently pure form and to avoid unnecessary loss. The process structure we consider is presented in Figure 1.
| Component | Flow | ||
|---|---|---|---|
| kmol s-1 | |||
| 1. | Benzene | \(C_6H_6\) | 0.97 |
| 2. | Chlorobenzene | \(C_6H_5Cl\) | 0.01 |
| 3. | Di-Chlorobenzene | p-\(C_6H_4Cl_2\) | 0.01 |
| 4. | Tri-Chlorobenzene | \(C_6H_3Cl_3\) | 0.01 |
| Pressure | 1 atm | ||
| Temperature | 313 K |
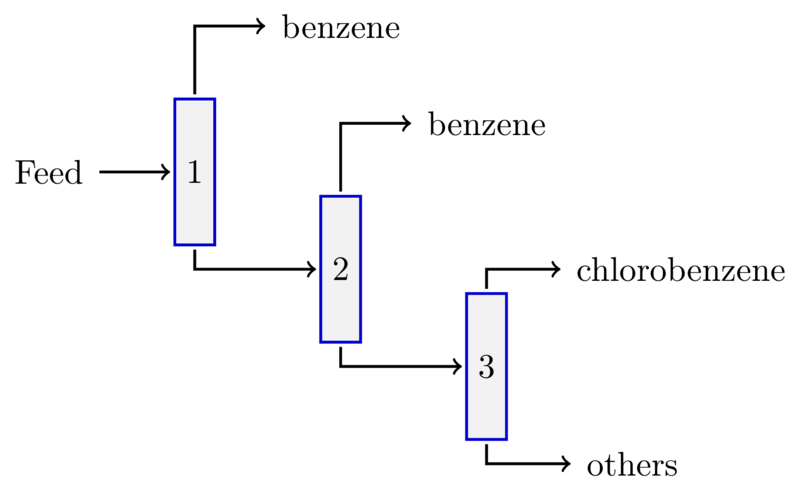
Figure 1: Process structure for the chlorobenzene purification stage showing three distillation units (numbered) with the desired product streams, benzene and chlorobenzene, and one waste stream, ``Others''.
To assess the different alternatives, the economic criteria of capital and operating costs are used. Process models are required to determine the impact of design decisions on these criteria. For this problem, the process models, in Jacaranda, are based on the Fenske, Underwood, and Gilliland short-cut models and correlations often used for multi-component distillation column design [Rathore et al. 1974; Monroy-Loperena and Vacahern 2012].
These models are based on the concept of light (most volatile component in the separation) and heavy (least volatile of the components) key species. Essentially, if the species in a mixture are sorted according to their boiling points, the mixture can be separated between any two adjacent species. For instance, if there were a mixture with three species, A, B, and C, with increasing boiling points from A to C, there would be two possible separations for this mixture. The first would be between A and B, yielding two streams, one with almost all of the A but a little B and one with a little of the A, most of the B, and essentially all of the C. The second separation possible would be between B and C: one of the resulting streams from this separation would have all the A, most of the B and a little C and the other stream would have a little B and most of the C.
The Fenske equation determines the minimum number of stages, \(N_{\min}\), a distillation column will require to achieve a given separation identified by the recovery of the light and the heavy:
\[ N_{\min} = \frac {\log \frac {x_{D,l}x_{B,h}} {x_{B,l}x_{D,h}}} {\log \alpha_{l,h}} \]
where \(D\) refers to the distillate or tops product of the distillation unit and \(B\) to the bottoms product. \(x\) is the molar fraction of each species in the streams, \(\alpha_{l,h}\) is the relative volatility of the light key to the heavy key. Volatility is a measure of the vapour pressure, a property of each species, with higher values of volatility associated with the lighter species. The relative volatility of a pair of species is the ratio of their volatilities.
The compositions of the light and heavy keys in the product streams are a function of the recovery design variable. The recovery specifies the fraction of the key species that ends up in the desired output stream. The higher the recovery, the smaller the amount of each key that goes out with the other stream. Higher recovery is required for higher purity of the final product streams but there is direct relationship between the recovery and the size of the distillation column and hence its cost, both capital and operating.
The Underwood equation determines the minimum amount of reflux, the liquid sent back into the column from the top stream to aid in achieving the separation:
\[ R_{\min} = \sum_{i=1}^{n_{c}} \frac {\alpha_{i} x_{D,i}} {\alpha_{i}-\theta} \]
where \(\theta\) is the solution to the nonlinear equation
\[ \sum_{i=1}^{n_{c}} \frac {\alpha_{i}x_{F,i}} {\alpha_{i} - \theta} = 1 - q\]
where \(F\) indicates the feed stream, \(n_{c}\) is the number of species involved in the feed stream and \(q\) is the state of the feed stream. The state depends on the energy in the stream and that is a function of the temperature and the pressure of the stream.
The actual number of stages, above the minimum \(N_{\min}\), and the actual reflux, also above the minimum \(R_{\min}\), are correlated through the Gilliland equation. This is also a nonlinear equation and depends on another design variable, the reflux rate factor. The higher the factor, the larger the actual reflux rate used. The reflux rate affects the operating costs through the use of cooling and heating utilities: larger reflux means increased utility use. It also influences the capital cost: higher reflux leads to a wider column but one with less stages, usually leading to a lower capital cost overall.
In all of the above equations, the calculation of variables such as \(\alpha\) and \(q\) require the estimation of physical properties. Physical property models are typically nonlinear. For this problem, we have used the Antoine equation to determine vapour pressures, \(p^{*}\) used to calculate the relative volatilities, \(\alpha\), of the species:
\[ \log p^{*} = A - \frac {B} {T - C} \]
where A, B and C are the Antoine coefficients which can be found in reference books for many species. The \(log\) function used will depend on the source of the Antoine coefficients and may be base 10 or natural.
The relative volatilities of the species are the ratio of their vapour pressure to one reference species in the mixture. The temperatures will depend on the operating pressure, the third design variable for the distillation unit. Higher pressures will results in higher temperatures and smaller relative volatilities. The former will affect the choice of heating and cooling utilities; the latter will affect the number of stages required for the separation required.
The process design has several constraints beyond the physical models described above. Firstly, the benzene and chlorobenzene product streams must meet purity requirements. Secondly, there is a finite number of utilities available for meeting the heating and cooling requirements. For some combinations of operating pressure and stream compositions, utilities may not be available to meet the requirements imposed by the design of the distillation units. Finally, there is a limit on how much of the main product, chlorobenzene, can be lost through the bottom product stream of the third distillation unit. The constraints define a feasible region that is small, well under 1% of the box domain defined by the design variable bounds. The small feasible region together with the nonlinear models can pose difficulties to optimization methods.
A more detailed description of the full model used is given in [Zilinskas et al. 2006].
3.2. The Jacaranda system
The Jacaranda system [Fraga et al. 2000] is an extensible object oriented framework for process design and optimization written in Java. It implements its own modelling suitable for the definition of complex process flowsheets with detailed processing step models. The process described in the previous section can be implemented in Jacaranda.
Jacaranda is available for download, with links and instructions for licensing detailed in the guide. Once downloaded, as a jar file, the CLASSPATH environment variable must be set to point to the jacaranda.jar file.
A package, Jacaranda.jl, is available to access Jacaranda and the objects created by that system. To add this package to your Julia configuration, simply invoke Julia in a command line or shell window:
$ julia julia> ] (@v1.7) pkg> add https://gitlab.com/ericsfraga/Jacaranda.jl [...] (@v1.7) pkg> BACKSPACE julia> ^d $
where the lines show the prompt you should be expecting at each point. The elided [...] output should show a number of packages being installed, those that Jacaranda.jl depends on. Once this has been done, you should be able to type the following in Julia:
1: using Jacaranda
3.3. The Jacaranda Chlorobenzene process model
In this section, we define the process model for the chlorobenzene recovery process. The model is written in the Jacaranda system modelling language. Each snippet of the model described here is tangled to an input file, clben-process-flowsheet.in, which will be used as input to the Jacaranda system. The structure of the process is described in section 3.1. It consists of a feed, two distillation columns, and three output streams. The Jacaranda model also defines an objective function based on specific defined criteria for optimization and the measure of constraint violations for infeasible solutions. This objective function provides the information necessary to be used by the nature inspired optimization methods developed in the previous chapter.
\sloppy The first part of the process model specification is administrative, asking for output from Jacaranda itself to be redirected to the specified file, clben-process-flowsheet.out and giving the project a name, clben-withconstraints. Two namespaces in the Jacaranda object framework are also specified. This allows us to write, for instance, Criteria instead of the fully qualified jacaranda.design.ps.Criteria. The first namespace is for process synthesis related objects and the second is for processing unit models.
output clben-process-flowsheet.outproject clben-withconstraintsuse jacaranda.design.psuse jacaranda.design.units
The next part of the process model specification is the definition of constants used by the remainder of the model definition. Also, some variables used by Jacaranda's own optimization subsystem are defined. Jacaranda was originally designed to implement an implicit search procedure for finding optimal process designs, using discretization and dynamic programming [Fraga 1996; Fraga and McKinnon 1994]. Although these settings are not relevant for the use in this book, they may be useful for comparing results with other published results [Zilinskas et al. 2006].
variablesconst Base 0.001 "Base flow discretization"# flows of species in feed streamconst Fbenzene 0.97 "Flow of Benzene"const Fc6h5cl 0.01 "Flow of C6H5Cl"const Fpc6h4cl2 0.01 "Flow of p-C6H4Cl2"const Fc6h3cl3 0.01 "Flow of C6H3Cl3"# set the cost base to 1993 based on the M&S indexset msindex 964.2const nPs 4 "Number of discrete enthalpy levels"end
For this process, we want to investigate the difference in operating versus capital costs so we define two criteria, each of which is the sum of the relevant criterion value generated by each unit in a flowsheet. The term in quotes for each criterion is the expression to evaluate for each unit. The sum means that the value of the criterion is the sum of expression evaluate for all the units in the resulting flowsheets.
Some criteria have been included which in fact are constraints on aspects of the process. The values of
compositionspec (composition purity requirements) and flowspec (maximum flow of contaminants allowed) represent the maximum violation of the inequality constraints for product specifications. The
value of UtilitySpec represents the temperature violation for heating and cooling utility requirements. All of these should be less than or equal to 0 for feasible solutions. Positive values give a measure of the infeasibility which can be used in assigning fitness to solutions in a population (see Section 2.2.3).
Criteria costscriterion CapitalCost sum "capcost"criterion OperatingCost sum "opercost"criterion CompositionSpec max "compositionspec"criterion FlowSpec max "flowspec"criterion UtilitySpec max "Tviolation"end
Next we define the heat exchanger model for heating and cooling. There are two cost functions, one for the capital cost as a function of the area of the exchanger and the other the operating cost as a function of the duty (Q [kJ]), the cost of the utility used (Cu [$/kJ]), and the time (seconds in a year equal to h*hpy where hpy is the operating hours per year). To cater for the case where the temperature differences at both ends of the exchanger are the same, we use the Chen approximation [Chen 1987] to avoid numerical issues in the log function.
HeatExchanger hexmodeldeltain = abs(T1in-T2out)deltaout = abs(T1out-T2in)eps = abs(deltain/deltaout-1)if eps < 4e-4lmtd = (1+eps/2-eps^2/12)*deltaoutelselmtd = (deltain - deltaout)/log(deltain/deltaout)endifA = Q/U/lmtdcapcost = 101964 + 92.9*A^0.65opercost = Cu*Q*h*hpyendend
Utilities are specified which may be used to meet the heating and cooling requirements of the processing units. The parameters for costing the use of a utility are the inlet temperatures of both the process stream and the utility itself, the outlet temperatures, the overall heat transfer coefficient for the exchange, and the cost of the utility per unit of heat. Each utility definition therefore includes its inlet and outlet temperatures, the heat transfer coefficient, and the cost.
Along with the actual utilities, we define two special utilities solely to provide penalty function information when none of the normal utilities is sufficient to meet the requirements of the processing unit. These special utilities will give a positive value for Tviolation should none of the actual heating or cooling utilities be suitable. The Tviolation will be used as one of the criteria defined above and will therefore be available for the optimization system to assign fitness values to infeasible process designs.
DiscreteUtilities utilshot "HotPenalty"Tin 1000Tout 1000htc "5000 *W/m^2/K"cost "1.0246 /GJ"modelTviolation = T1out - 503.5endendhot "Steam @28.23 atm" 503.5 503.5 "5000 *W/m^2/K" "1.0246 / GJ"hot "Steam @11.22atm" 457.6 457.6 "5000 *W/m^2/K" "0.773824 / GJ"hot "Steam @ 4.08atm" 417.0 417.0 "5000 *W/m^2/K" "0.573203 / GJ"hot "Steam @ 1.70atm" 388.2 388.2 "5000 *W/m^2/K" "0.41796 / GJ"cold "ColdWater @ 32.2degC" 305.2 305.2 " 500 *W/m^2/K" "0.0668737 / GJ"cold "Ammonia @ 1degC" 274.00 274.00 " 500 *W/m^2/K" "1.65035 / GJ"cold "Ammonia @ -17.68degC" 255.32 255.32 " 500 *W/m^2/K" "2.96871 / GJ"cold "Ammonia @ -21.67degC" 251.33 251.33 " 500 *W/m^2/K" "3.96226 / GJ"cold "ColdPenalty"Tin 0Tout 0htc "500 *W/m^2/K"cost "3.96226 /GJ"modelTviolation = 251.33-T1outendendend
Note that the utilities have been defined in decreasing order of temperature.
All the data we need for this problem have been defined. Now set the global data variables that are used by the process evaluation procedure:
Datacriteria costshex hexutils utilsend
Given these data, we can now define the actual process flowsheet. This process consists of three distillation columns and four specific product tanks, as well as a feed tank (Figure 1).
The first unit is the feed tank. Associated with this tank is the actual feed stream. The feed stream consists of the output of the reactor and there are 4 different components (molecular species). All the components
of the stream are defined using the KistaComponent class. This component class uses physical properties estimation methods [Ponton 1989; Boston and Britt 1978] based on the 1 atm boiling point of the component and the coefficients of the vapour heat capacity polynomial correlation.
vle.KistaComponent benzenebp 353.2cpv -33.917 4.743e-1 -3.017e-4 7.130e-8lhtc " 500 *W/m^2/K"vhtc "5000 *W/m^2/K"endvle.KistaComponent C6H5Clbp 405.2cpv -33.888 5.631e-01 -4.521e-04 1.426e-07lhtc " 500 *W/m^2/K"vhtc "5000 *W/m^2/K"endvle.KistaComponent p-C6H4Cl2bp 447.3cpv -14.344 5.534e-01 -4.559e-04 1.447e-07lhtc " 500 *W/m^2/K"vhtc "5000 *W/m^2/K"endvle.KistaComponent C6H3Cl3bp 486.2cpv -14.361 6.087e-01 -5.622e-04 2.072e-07lhtc " 500 *W/m^2/K"vhtc "5000 *W/m^2/K"end
Using these components, we can now define the feed stream. This stream consists of a single phase at specified
temperature and pressure conditions. To define the stream, we first define the Phase object with the
correct amounts of each component.
In defining the Phase object, we also specify the granularity of the component flows for each component. This is the basic discretization used by Jacaranda to ensure that the search graph generated implicitly is finite in size. The granularity should be appropriate for the particular problem and, in particular, should be consistent with discretizations performed in the separation units (for example) and the product specifications. In this problem, we have specified the same discretization factor (Base as defined above) for each component as a function of its flow in the feed stream. The individual flows of the components in the feed stream have been defined in the main input file as well. However, it should be noted that the discretization settings are not used in the case study presented below. They are here for completeness should an interested reader wish to experiment with Jacaranda itself directly.
vle.Phase feedPhaseadd benzene Fbenzeneadd C6H5Cl Fc6h5cladd p-C6H4Cl2 Fpc6h4cl2add C6H3Cl3 Fc6h3cl3base benzene "Base * Fbenzene"base C6H5Cl "Base * Fc6h5cl"base p-C6H4Cl2 "Base * Fpc6h4cl2"base C6H3Cl3 "Base * Fc6h3cl3"showend
The stream definition includes the phase object defined above and the specification of the state of the stream. The state is defined by the initial temperature and pressure and the number of discrete pressure levels which can be represented. This number, nPs, is defined above.
vle.Stream feedadd feedPhasenstates nPsT 313P "1 *atm"end
Given the feed stream, we can now define the feed tank unit: this is a unit with no input streams and one output stream, the feed to the process.
vle.FeedTank feedtank-1Stream feed feedend
The feed stream is sent to a distillation column, dist-2. This unit will separate the mixture in the feed stream, using benzene as the light key. The distillation model defines a number of design variables that will be used by the optimization procedures: rrf, the reflux rate factor, rec, the recovery of the light and heavy keys, and P, the operating pressure of the column:
vle.Distillation dist-2Component key benzeneReal rrf 1.2 1.05 1.5 10Real trayefficiency 1.0 1.0 1.0 1Boolean eduljee falseBoolean conceptual falseBoolean sfa falseBoolean totalcondenser truenew tunable+specification "Recovery of light and heavy keys" Real rec 0.95 0.800 0.999 10LogReal P 5.039684199579494 1.0 32.0 16end
The top product of the first distillation will go into a product tank, intended to receive pure benzene. The benzene is eventually destined to be recycled back to the reaction section in the upstream process. The recycle is not considered in this problem. The specification is that the benzene be at least 98 mole% pure (compositionspec) and for there to be no more than 0.005 kmol s-1 of chlorobenzene (flowspec).
vle.ProductTank pureBenzene-3Expression spec "1"modelcompositionspec = 0.98-x[benzene]flowspec = F*x[C6H5Cl] - 0.005endend
The second distillation column, which processes the bottom product of the first distillation unit, also has benzene as the light key and the same three design variables for optimization:
vle.Distillation dist-4Component key benzeneReal rrf 1.2 1.05 1.5 10Real trayefficiency 1.0 1.0 1.0 1Boolean eduljee falseBoolean conceptual falseBoolean sfa falseBoolean totalcondenser truenew tunable+specification "Recovery of light and heavy keys" Real rec 0.999 0.800 0.999 10LogReal P 32.0 1.0 32.0 16end
The top product stream, intended to be pure benzene, is sent to another product tank that has the same composition and flow specifications: 98 mole% benzene with no more than 0.005 kmol s-1 of chlorobenzene:
vle.ProductTank pureBenzene-5Expression spec "1" # always truemodelcompositionspec = 0.98-x[benzene]flowspec = F*x[C6H5Cl] - 0.005endend
The third and final distillation unit separates chlorobenzene from the waste products.
vle.Distillation dist-6Component key C6H5ClReal rrf 1.2 1.05 1.5 1Real trayefficiency 1.0 1.0 1.0 1Boolean eduljee falseBoolean conceptual falseBoolean sfa falseBoolean totalcondenser truenew tunable+specification "Recovery of light and heavy keys" Real rec 0.95 0.800 0.999 10LogReal P 1.5874010519681996 1.0 32.0 16end
The top product from this distillation unit is sent to a product tank with the specifications for the chlorobenzene, specifically a purity of at least 90 mole% (compositionspec).
vle.ProductTank pureC6H5Cl-7Expression spec "1" # always truemodelcompositionspec = 0.90-x[C6H5Cl]endend
The bottom product from the third distillation unit is sent to another product tank. This tank has a constraint that there be no more than 10 mole% benzene or 10 mole% chlorobenzene.
vle.ProductTank otherProducts-8Expression spec "1" # always truemodelcompositionspec = max({x[benzene]-0.10, x[C6H5Cl]-0.10})endend
Having defined all the processing steps in the process, including feed and product tanks and the actual processing steps, we define the actual Flowsheet object which consists of the units and their connections:
Flowsheet clbenbuildfeedtank-1 dist-2dist-2 pureBenzene-3 dist-4dist-4 pureBenzene-5 dist-6dist-6 pureC6H5Cl-7 otherProducts-8endcontinuousevaluationmethod breadthfirstend
The continuous specification means that the discretization parameters defined in this model are not taken into account. Jacaranda's Flowsheet object can model the process in both continuous and discrete spaces. For the purposes of this book, only the continuous modelling is considered.
This completes the definition of the clben process flowsheet in Jacaranda. In the next section, the model is accessed through the Jacaranda-Julia interface, retrieving the clben object to be able to evaluate the process with different values for the design variables.
3.4. The Chlorobenzene process objective function
The first step in defining the objective function for the chlorobenzene process design problem is to use Jacaranda to load the process flowsheet object, defined in the previous section:
1:function process()2:Jacaranda.init("clben-process-flowsheet.in", "clben")3:end
The Jacaranda.init function loads the input file given as the first argument. The second argument is the name of the Jacaranda variable that implements the ObjectiveFunction interface (in the jacaranda.util.opt namespace). The Flowsheet object implements that interface. The Jacaranda.init method returns the following 5-tuple:
(flowsheet, x0, lower, upper, nf)
where flowsheet is a handle on the Jacaranda process flowsheet object. The remaining entries in the tuple relate to the flowsheet itself. x0 is an initial guess for the design variables. These initial values are those specified in the definition of the flowsheet and its processing units in the Jacaranda input file. lower is the vector of lower bounds on the design variables, upper the vector of upper bounds, and nf the number of objective function values that will be returned when the process flowsheet is evaluated.
The design variables for this process are the design variables for each distillation unit: the operating pressure, P \(\in [1, 32]\) atm, the reflux rate factor, rrf \(\in [1.05, 1.5]\), and the recovery of the light and heavy keys, rec \(\in [0.8, 0.999]\). As there are three distillation units, there are 9 design variables.
The objective function values, as returned by the evaluation of the process flowsheet, include not just the criteria values used to assess the particular design alternative but also the violations of any constraints, e.g. product purity. These are defined in the Criteria object. For the chlorobenzene process, there are 5 criteria in total. Two of these, the capital cost and the operating cost, are actual objective values for optimization and the other three are feasibility constraints. Therefore, when we evaluate the process flowsheet, we split the values returned into the objective function values, as a vector with two values, and a single feasibility indication, as the maximum of the constraint violations:
1:function evaluate(v, flowsheet)2:f = Jacaranda.evaluate(flowsheet, v)3:# Jacaranda returns, for this process, two4:# objective function values and three5:# constraint violations so put these in the6:# form that an optimization system can use7:(f[1:2], maximum(f[3:5]))8:end
3.5. Example evaluation
The following code illustrates the use of the evaluate function. The process flowsheet is evaluated at four different points in the search space: the initial guess defined in the Jacaranda input file, x0, the lower and the upper bounds, and at a mid-point between these bounds.
1:using NatureInspiredOptimization.Chlorobenzene: process, evaluate2:flowsheet, x0, lower, upper, nf = process()3:[evaluate(x0, flowsheet)4:evaluate(lower, flowsheet)5:evaluate(upper, flowsheet)6:evaluate(lower + (upper-lower)/2.0, flowsheet)]
The results, below, show the results for each of the four evaluations. Each line consists of the two objective function values, within square brackets, and the measure of constraint evaluation.
4-element Vector{Tuple{Vector{Float64}, Float64}}:([2.1074435175185073e6, 3.512848134293994e6], 149.3968323935136)([1.989911840550072e6, 1.3787081622759001e6], 0.7885017421602787)([2.6923280544667e6, 6.012089599489303e6], 463.7476422252121)([1.7892859471243918e6, 4.264066021597366e6], 236.37180766744075)
The first line tells us that the value returned is a vector with four elements. Each element, as expected, is a tuple (with the objective function values) and a real number (the constraint violation). None of the four points evaluated is feasible. One of the challenges of this problem is finding feasible points and any optimization search procedure will need to be able to start with infeasible solutions and hopefully eventually identify feasible solutions on its route to finding a good design.
3.6. Results
Having defined the Jacaranda process flowsheet object, and tested it, we can now consider applying each of the optimization methods to find the best design. In the cases that follow, all codes have the same preamble for this problem, which we define here:
1:using Jacaranda2:using NatureInspiredOptimization.Chlorobenzene: process, evaluate3:4:# define the process flowsheet5:flowsheet, x0, lower, upper, nz = process()
This preamble, as in the example above, creates the Jacaranda process object and defines variables for the optimization methods, including lower and upper bounds for the search domain. An initial point in the search, x0, has been defined and will be used although it has no special significance. As we have seen above, this point does not yield a feasible design. Further, it has objective function values (in so much as these mean anything for an infeasible design) that are not necessarily good when compared with the values obtained for the lower bounds, upper bounds, or mid-point values of the design variables.
3.6.1. Single objective function case
Although the design of the chlorobenzene process has been defined as a multi-objective optimization problem, we consider first a single objective version. The single objective is the sum of the two cost criteria: the capital cost and the annual operating cost. This is equivalent to considering the capital cost amortised over a period of 1 year which is arguably not reasonable but is fine for testing the performance of the different methods.
1:# single criterion objective function2:function single(v, flowsheet)3:f = Jacaranda.evaluate(flowsheet, v)4:# combine the two objective function values5:# into a single objective6:([f[1]+f[2]], maximum(f[3:5]))7:end
Note that this objective function expects two arguments, the design variables and the flowsheet. This case illustrates the use of the parameters optional argument, available in all of the methods implemented in the previous chapter, to pass the flowsheet Jacaranda object to the objective function for evaluation.
All the methods will be limited to 105 evaluations of the objective function. This is a reasonable limit given the computational complexity of the process simulation.
3.6.1.1. Random search
As a basis for comparison, we use the random search method, evaluating solutions obtained by a random sampling in the box defined by the lower and upper bounds on the design variables for this process. The method is applied 10 times to cater for the method's stochastic nature:
1:using NatureInspiredOptimization: randomsearch2:# number of objective function evaluations3:nf = 100_0004:for run ∈ 1:105:starttime = time() # wall clock time6:best = randomsearch(7:single, # objective function8:parameters = flowsheet, # for evaluation9:lower = lower, # lower bounds10:nfmax = nf, # max evaluations11:upper = upper # upper bounds12:)13:deltatime = time() - starttime # elapsed time14:println("final: $run $nf $deltatime $(best.z) $(best.g)")15:end
| run | z | g | feasible |
|---|---|---|---|
| [M$] | |||
| 1 | 5.33 | 0.000 | yes |
| 2 | 4.89 | 0.066 | no |
| 3 | 5.24 | 0.030 | no |
| 4 | 5.73 | 0.000 | yes |
| 5 | 5.63 | 0.000 | yes |
| 6 | 5.09 | 0.107 | no |
| 7 | 5.12 | 0.000 | yes |
| 8 | 5.27 | 0.012 | no |
| 9 | 5.40 | 0.014 | no |
| 10 | 5.28 | 0.000 | yes |
The results of solving the problem 10 times are summarised in Table 1. The best feasible result is 5.12 × 106. Half of the runs obtain a feasible solution but half do not. Note that lines 5 and 13 are used to determine the amount of time spent in the search. This time is similar for all methods because, for process systems engineering problems, the computational effort is mostly in the evaluation of the objective function and not the actual search methods. As a results, there will be no further reference to the computational times.
Noting the failure to find feasible solutions in half of the attemps, we consider sampling the space with 107 points to gain insight into the size of the feasible domain for this problem. This function evaluates the space randomly:
1:using NatureInspiredOptimization: Point, randompoint2:# number of objective function evaluations3:nf = 10_000_0004:feasible = 05:infeasible = 06:for i ∈ 1:nf7:global feasible8:global infeasible9:p = Point(randompoint(lower,upper), single, flowsheet)10:if p.g ≤ 0.011:feasible += 112:else13:infeasible += 114:end15:if rem(i,10000) == 016:print(stderr, "$i = $feasible+$infeasible, $(round(100*infeasible/i))% \r")17:end18:end19:println("At end, $feasible points found out of $nf in total.")
This sampling finds only 60 feasible points, for a rate of 6 in a million. This is consistent with the results obtained above as we would expect, on average, 0.6 of the runs with \(n_f=10^5\) to find a feasible solution. The conclusion is thta the feasible domain is a very small part of the full domain defined by the bounds on the 13 design variables.
The shape of the feasible region is unknown but we have some belief that it is contiguous and may actually be convex.2 This would mean that, should a single feasible point be found, some search methods should be able to find good solutions. One positive attribute of this case study is that the violation constraints have physical meaning and searching in the part of the domain consisting of infeasible solutions should lead to feasible points in attempting to minimise the constraint violation (see Section 2.2.3).
3.6.1.2. Genetic algorithm
As the genetic algorithm uses crossover to create new members of the population much more frequently than through mutation, we start the problem with a population consisting of the points we evaluated for testing the implementation of the chlorobenzene process in a previous chapter.
1:using NatureInspiredOptimization: Point2:p0 = [Point(x0, single, flowsheet)3:Point(lower, single, flowsheet)4:Point(upper, single, flowsheet)5:Point(lower + (upper-lower)/2, single, flowsheet)]
The genetic algorithm has three tunable parameters: the population size, the crossover rate, and the mutation rate. As this is the first real problem attempted, the problem is therefore solved for a number of alternative values for each of these parameters. This should allow us to gain some insight into which parameter values might be appropriate for this type of problem. Generalising from one case study, however, is not possible. The need to tune parameter settings is often an issue with nature inspired optimization methods.
Note, that as in the random search case above, the problem will be solved 10 times for each combination of parameter values to see the effect of the stochastic nature of the method.
1:using NatureInspiredOptimization.GA: ga2:nf = 100_0003:for np ∈ [10 50 100]4:for rc ∈ [0.3 0.5 0.7 0.9]5:for rm ∈ [0.01 0.05 0.1 0.2]6:for run ∈ 1:107:starttime = time()8:best, p, ϕ = ga(9:p0, # initial population10:single, # objective function11:parameters=flowsheet,12:lower=lower, # lower bounds13:upper=upper, # upper bounds14:nfmax = nf, # max function evals15:np = np, # population size16:rc = rc, # crossover rate17:rm = rm # mutation rate18:)19:deltatime = time() - starttime20:println("final: $run $nf $np $rc $rm $deltatime $(best.z) $(best.g)")21:end22:end23:end24:end
Figure 1: The objective function of the best solution obtained for all the runs, as a function of the crossover (\(r_c\)) and mutation (\(r_m\)) rates, with \(n_f=100000\) and different population sizes (\(n_p=\)10, 50, 100). Ten runs for each combination of parameter values were performed.
The results of this code are summarised in Figure 1 where the impact of the three parameters, \(n_p\), \(r_c\), and \(r_m\), is seen on the value of the objective function for the best solution identified in each run. Except for the case of \(r_c=0.9\) and \(r_m=0.2\), there is significant variation on the outcome. The results for \(r_c=0.9\) and \(r_m=0.01\) have been truncated as some outcomes were significantly higher (worse). The best solution obtained was 3.7957 × 106, obtained only once with \(n_p=10\), \(r_c=0.7\), and \(r_m=0.2\). Many attempts resulted in values around 3.84 × 106, as can be seen by the cluster of points at the bottom of each impulse in the plot. However, for each combination of parameter values, solutions 10-15% worse than the best known are obtained. The most consistent outcome was obtained with \(r_m=0.05\).
Figure 1: Typical evolution profile for the chlorobenzene design problem using the genetic algorithm as a function of the number of objective function evaluations, \(n_f\).
Figure 1: The evolution for the best solution obtained from all the runs for the GA attempting the chlorobenzene process design problem showing two stages of the evolution. The first stage is the search for a feasible solution and the second stage is improving on such when found. For the first two to three thousand evaluations of the objective function, no feasible solution is found. After a feasible solution is found, the GA converges quickly to a good solution.
Figure 1 shows a typical profile for a case where a good solution is obtained. More interesting is the evolution for the best case (described above), shown in Figure 1. For the first 2000 or so function evaluations (\(n_f\), the \(x\)-axis), no feasible solutions are present in the population. The dotted graph shows the evolution of the best solution in terms of the measure of constraint violation (left \(y\)-axis). The initial value of the constraint violation, 0.7885, is that obtained with the lower bounds on all the variables (see example results in section 3.5). Once a feasible solution is found, the graph on the right of the plot presents the value (right \(y\)-axis) of the objective function. For infeasible solutions, the value of the objective function is meaningless.
3.6.1.3. Particle swarm optimization
As in the case for the genetic algorithm, the PSO will also start with an initial population, using the code block clbeninitpop defined above.
For the PSO method, parameters include:
- \(n_p\)
- the population size, i.e. the number of particles in the swarm. Note that the PSO implementation will ensure that the starting population has this size regardless of the initial population passed to it.
- \(\omega\)
- the inertia: how much of the current velocity to include in the calculation of the new velocity. The original PSO algorithm had \(\omega=1\) but it might be useful to try different values.
- \(c_1\)
- the weighting on the velocity change due to the relative position of the particle and the particle's best solution to date.
- \(c_2\)
- the weighting on the velocity change due to the relative position of the particle and the best point found by the whole swarm to date.
1:using NatureInspiredOptimization.PSO: pso2:nf = 100_0003:for np ∈ [10 50 100]4:for ω ∈ [0.5 1.0] # inertia5:for c₁ ∈ [1.0 1.5 2.0] # particle best6:for c₂ ∈ [1.0 1.5 2.0] # global best7:for run ∈ 1:108:starttime = time()9:best, p = pso(10:p0, # initial population11:single, # objective function12:parameters=flowsheet, # for evaluation13:lower=lower, # lower bounds14:upper=upper, # upper bounds15:ω = ω,16:c₁ = c₁,17:c₂ = c₂,18:nfmax = nf, # max function evals19:np = np # population size20:)21:deltatime = time() - starttime22:println("final: $run $nf $np $ω $c₁ $c₂ $deltatime $(best.z) $(best.g)")23:end24:end25:end26:end27:end
The results indicate that both the population size and the value of ω have a significant impact on the performance of the method. For this case study, all combinations of parameters where the population is less than 100 and ω less than 1 lead to poor results, including not finding a feasible solution at all in many attempts. The population size needs to be larger to ensure that enough diversity is retained for long enough to get to a good solution. The value of ω also ensures that the change in velocity is gradual, slowing down the convergence to a local optimum.
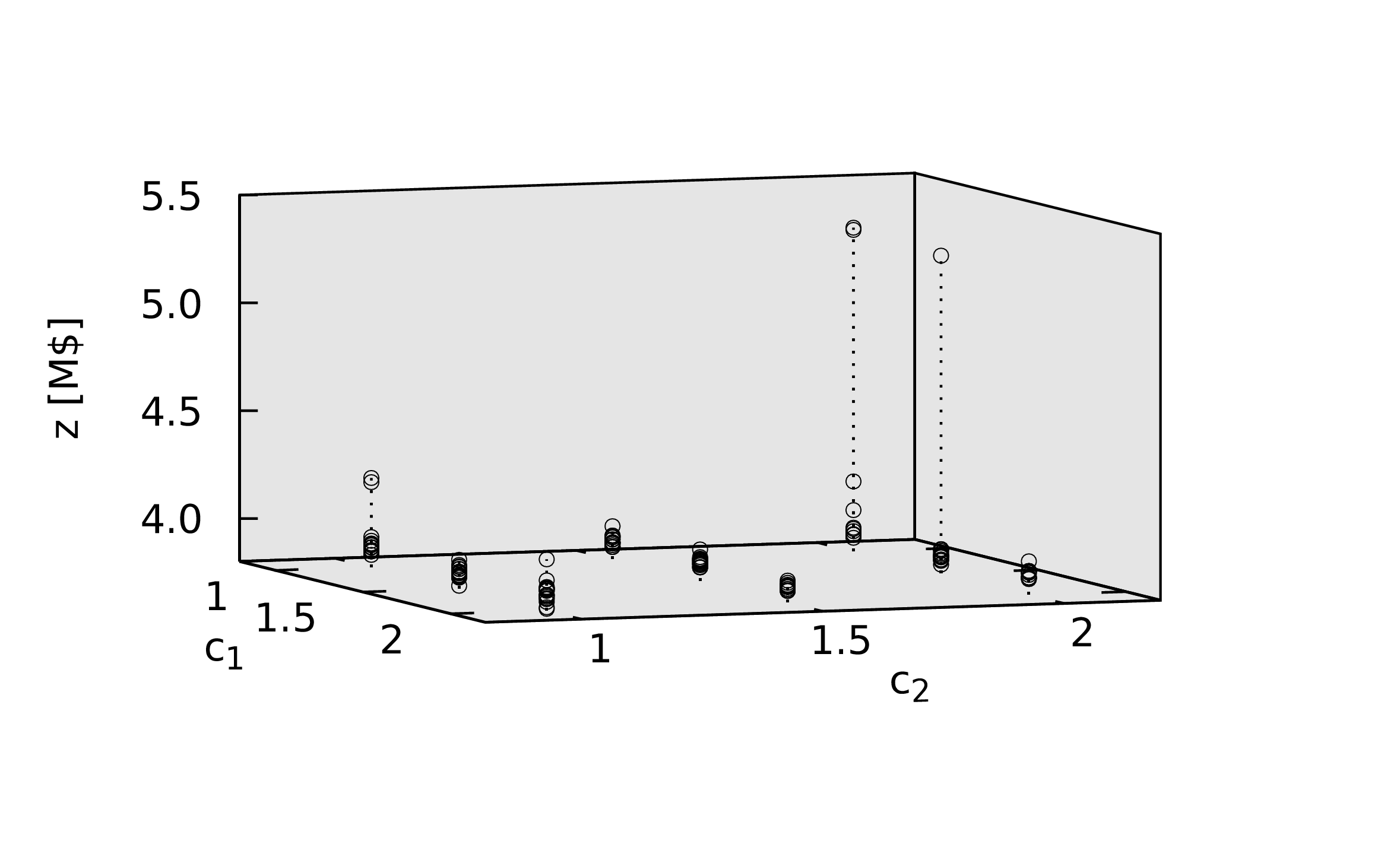
Figure 1: Outcomes from using the PSO method to solve the single objective chlorobenzene design problem with \(n_p=100\) and \(\omega=1\) for different values of the weights on the distance to best particle solution and the best solution known to the population.
Figure 1: The evolution profile for the PSO method for the chlorobenzene process design problem, illustrating the quick convergence to a local optimum.
Figure 1 shows the performance of the PSO method with \(n_p = 100\) and \(\omega = 1\) for different combinations of the two weightings, \(c_1\) and \(c_2\). Even for these values, one run was unable to find a feasible solution at all. Figure 1 shows the evolution of one of the better runs with feasible solutions found by the second iteration (200 function evaluations). The method converges to a solution quickly, by 1000 function evaluations, with only a small amount of correction thereafter.
Overall, the performance of the PSO is not promising, showing premature convergence to not necessarily good solutions. This is a known disadvantage of the PSO method:
Although the principle of multi-objective particle swarm optimization is simple and the operability is strong, it is still prone to local convergence and the convergence accuracy is not high. [Zhang et al. 2022]
However, when good solutions are found, they are found quickly so the PSO method appears useful for quick searches. It should be noted that the PSO method has been adapted to address premature convergence; see [Niu and Shen 2007; Coello et al. 2004] for methods which add mutation and also address multi-objective problems, which the implementation in this book does not.
3.6.1.4. Plant propagation algorithm
As in the case for genetic algorithms, the PPA will also start with an initial population, using the code block clbeninitpop defined above. The PPA has two tunable parameters: the population size and the maximum number of runners to generate for a selected solution. Again, each combination of values for these parameters is attempted 10 times to investigate the variability of the outcomes.
1:using NatureInspiredOptimization.PPA: ppa2:nf = 100_0003:for np ∈ [10 50 100]4:for nrmax ∈ [3 5 10 20]5:for run ∈ 1:106:starttime = time()7:local best8:local p9:local ϕ10:best, p, ϕ = ppa(11:p0, # initial population12:single, # objective function13:parameters=flowsheet,14:lower=lower, # lower bounds15:upper=upper, # upper bounds16:nfmax = nf, # max evals17:np = np, # population size18:nrmax = nrmax, # max runners19:)20:deltatime = time() - starttime21:println("final: $run $nf $np $nrmax $deltatime $(best.z) $(best.g)")22:end23:end24:end
Figure 1: The outcomes obtained for 10 runs for each combination of parameters for the PPA, applied to the chlorobenzene process design optimization problem. The parameters are the population size, \(n_p\), the number of members of the population chosen to propagate in each iteration, and \(n_r\), the maximum number of runners to generate for each solution chosen for propagation.
The results of exploring the different values of the parameters are summarised in Figures 1 and 1. The first of these figures shows that for most combinations of the parameter values, the PPA is able to find good solutions with greater consistency than any of the other methods. The exceptions are with the larger number of runners allowed together with a larger population. For the PPA, the best combinations of parameters are lower population, e.g. \(n_p = 10\), with a limit on the number of runners to generate of 3 or 5.
Figure 1: The evolution of the best solution in the population as a function of the number of objective function evaluations. Initially, the best solution is that with the least constraint violation, implying that the population consists solely of infeasible designs. After some time before 2000 objective function evaluations, a feasible solution is obtained and the population improves consistently until a very good solution is obtained.
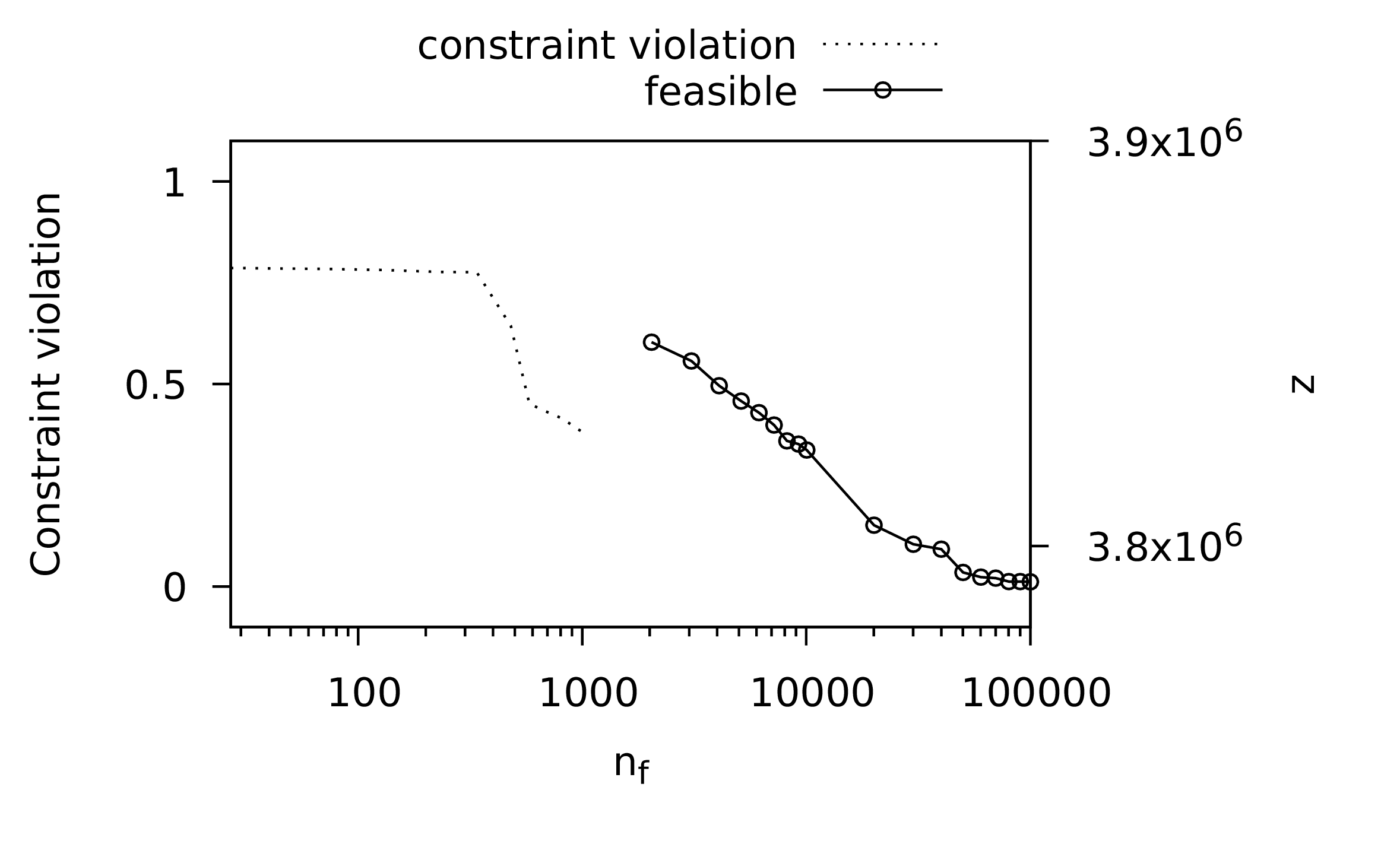
Figure 1: Evolution profile of the best solution obtained with the PPA for the chlorobenzene process design problem, with \(n_p=10\) and \(n_{r,\max}=10\).
Figure 1 shows the evolution of a typical run. A feasible solution is found after a thousand evaluations of the objective function and then the method converges to a good solution. In fact, the PPA is able to find the best solution out of the methods tried, with an objective function value of 3.791 × 106 M$. The evolution profile for this run is presented in Figure 1. Solutions with similar values are obtained frequently.
3.6.2. Multi-objective case
The chlorobenzene process design problem is naturally a multi-objective optimization problem. In the previous section, we considered a single objective version by combining two objectives into one with an equal weighting. Solving the multi-objective problem directly enables the design engineer to gain insight into the aspects that affect the individual criteria, aiding in the decision process should the relative importance of the criteria be unknown a priori.
This code defines a bi-criteria problem:
1:# single criterion objective function2:function biobjective(v, flowsheet)3:f = Jacaranda.evaluate(flowsheet, v)4:# two objective function values5:([f[1], f[2]], maximum(f[3:5]))6:end
The multi-objective nature of the objective function is indicated by having the first entry of the tuple be a two element vector instead of a single result (line 5).
The GA and PPA methods are easily adapted to multi-objective optimization problems so long as the fitness evaluation takes into account the different ranking required. The fitness evaluation method implemented above, Section 2.2.3, does support multiple criteria.
The PSO method as initially described and implemented above, however, cannot be used directly for multi-objective problems because of the need to determine directions to the historical best solutions, both for the individual particle and the population as a whole. Such a direction is not well-defined for a multi-objective problem as the best solutions are not individual points but sets of non-dominated points. However, a number of extensions and adaptations of the PSO method have been considered; see [Cui et al. 2022; Zhang et al. 2022; Shu et al. 2022; Zheng and Chen 2013; Feng et al. 2019; Ab Aziz et al. 2011] for some papers on this topic. The multi-objective problem could be solved as a series of single objective problems, either by combining the two objectives using a weighting that changes or through the ε-constraint method [Haimes 1971]. Nevertheless, only the GA and PPA methods will be used for the multi-objective process design problem.
The GA and PPA methods will use the same initial population, one which mirrors that used for the single objective case:
1:using NatureInspiredOptimization: Point2:p0 = [Point(x0, biobjective, flowsheet)3:Point(lower, biobjective, flowsheet)4:Point(upper, biobjective, flowsheet)5:Point(lower + (upper-lower)/2, biobjective, flowsheet)]
Again, recall that none of these points in the initial population is feasible.
3.6.2.1. Genetic algorithm
Multi-objective optimization problems require significantly more computational effort than single objective problems. The primary reason for this is the need for a sufficiently representative approximation to the Pareto frontier within the population. The approximation should have breadth, hopefully including the end points which correspond to the best outcomes for each individual criterion. The approximation should also be dense, that there are not large gaps from one solution to another along the frontier. As a result, population based method will require larger populations to capture the Pareto frontier.
A larger population and the need to evolve the approximation to the Pareto frontier also imply the need for more function evaluations. Therefore, we will consider up to 5 times as many objective function evaluations.
1:using NatureInspiredOptimization: hypervolume, nondominated, printpoints, printvector2:using NatureInspiredOptimization.GA: ga3:for nf ∈ [250000 500000]4:for np ∈ [50 100 250]5:for rc ∈ [0.3 0.5 0.7 0.9]6:for rm ∈ [0.01 0.05 0.1 0.2]7:for run ∈ 0:98:starttime = time()9:local best10:local hv11:local p12:local pareto13:local ϕ14:best, p, ϕ = ga(15:p0,16:biobjective,17:parameters=flowsheet,18:lower=lower,19:upper=upper,20:nfmax = nf,21:np = np,22:rc = rc,23:rm = rm24:)25:deltatime = time() - starttime26:println("best = $best")27:printpoints("population", p)28:printvector("fitness: ", ϕ)29:println()30:pareto = nondominated(p)31:printpoints("pareto", pareto)32:hv = hypervolume(pareto)33:println("final: $run $nf $np $rc $rm $deltatime $hv")34:end35:end36:end37:end38:end
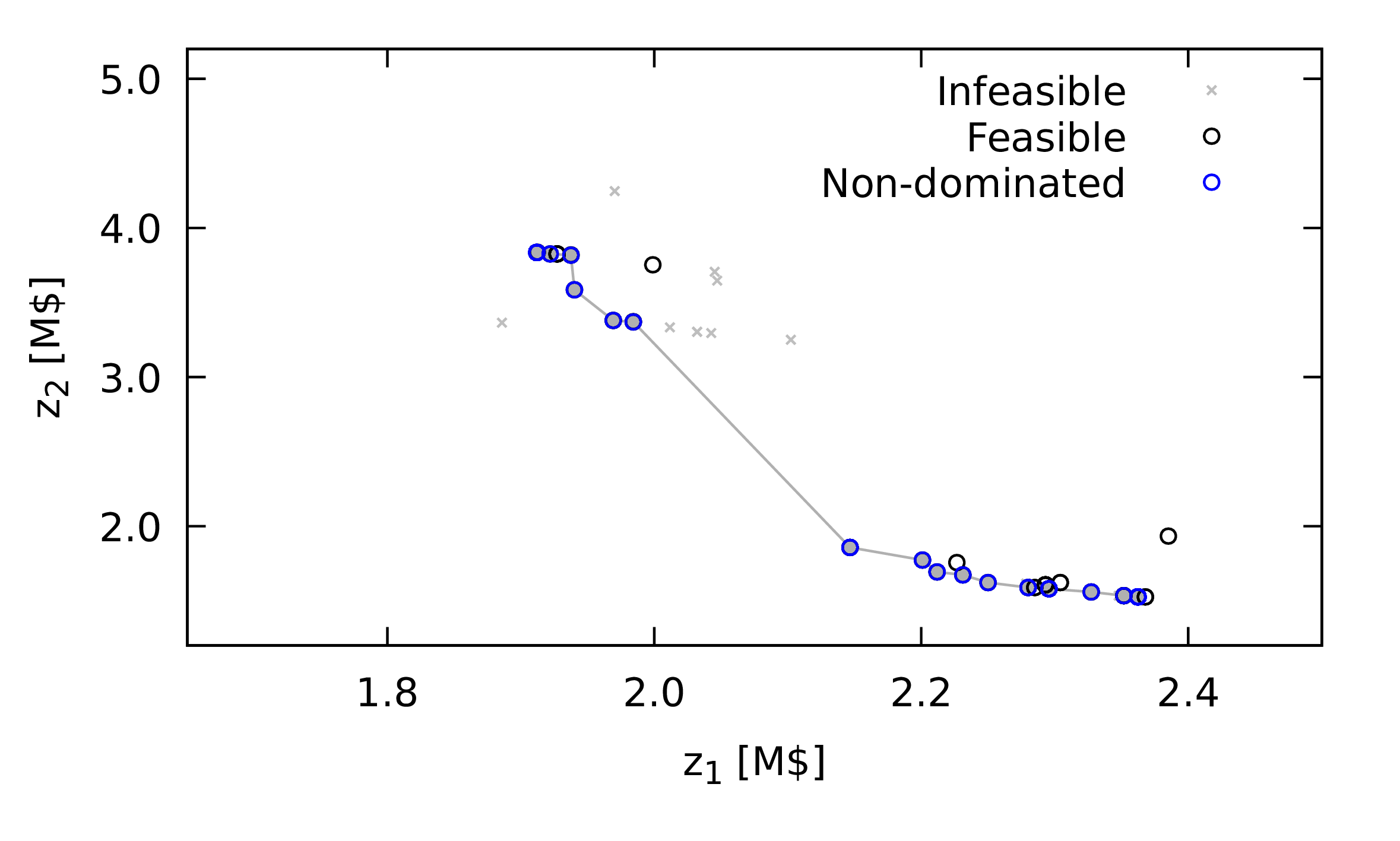
Figure 1: The final population for the GA solving the chlorobenzene multi-objective process design problem, obtained with \(n_p=100\), \(r_c=0.3\), and \(r_m=0.2\). The final population contains both feasible and infeasible points. The hyper-volume measure is 0.0892.
Figure 1 shows the final population obtained with the GA. The final population is shown in objective function space: the \(z_1\) axis is the capital cost of each solution and \(z_2\) is the annual operating cost. This final population contains both feasible and infeasible points. The non-dominated set of points is highlighted.
3.6.2.2. Plant propagation algorithm
As with the GA, the PPA will require more function evaluations and a larger population to characterise the Pareto frontier.
1:for nf ∈ [250000 500000]2:for np ∈ [50 100 250]3:for nrmax ∈ [5 10]4:for run ∈ 0:95:starttime = time()6:local best7:local hv8:local p9:local pareto10:local ϕ11:best, p, ϕ = ppa(12:p0,13:biobjective,14:parameters=flowsheet,15:lower=lower,16:upper=upper,17:nfmax = nf,18:np = np,19:nrmax = nrmax,20:)21:deltatime = time() - starttime22:println("best = $best")23:printpoints("population", p)24:printvector("fitness: ", ϕ)25:println()26:pareto = nondominated(p)27:printpoints("pareto", pareto)28:hv = hypervolume(pareto)29:println("final: $run $nf $np $nrmax $deltatime $hv")30:end31:end32:end33:end
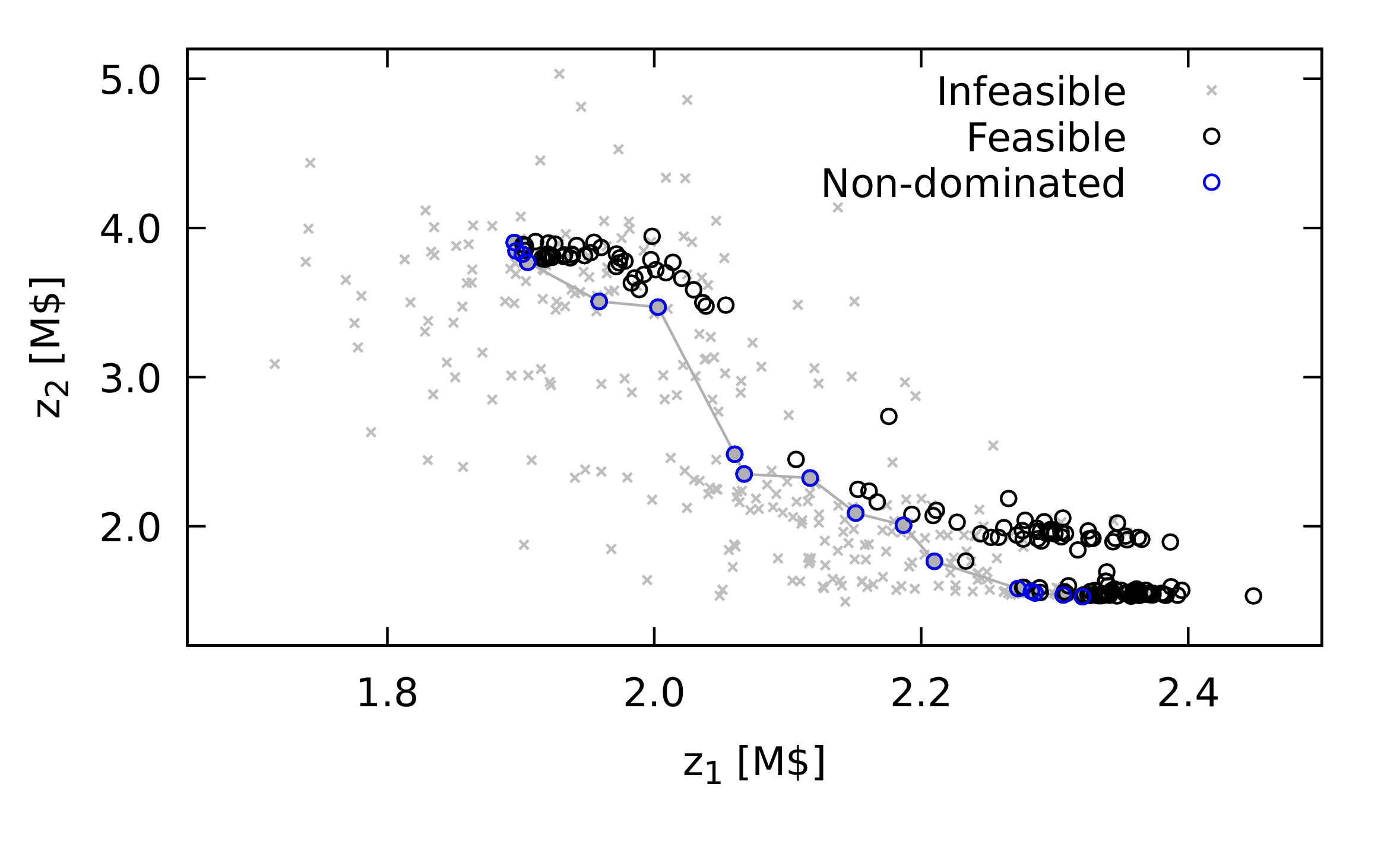
Figure 1: Plot of final population for the PPA applied to the chlorobenzene process design problem considering multiple objectives. This the outcome with \(n_p=100\) and \(n_{r,\max}=10\), after 500 thousand evaluations of the objective function. The set of non-dominated feasible solutions has been highlighted. The hyper-volume measure is 0.0784.
Figure 1 shows an example of the outcome of applying the PPA to the chlorobenzene process design problem with two objectives. The final population is shown in objective function space. The set of non-dominated feasible points is highlighted. The figure shows that the final population is diverse and continues to include many infeasible solutions.
The breadth of the set of non-dominated points is good as is the distribution over the approximation to the Pareto frontier. However, the remaining set of feasible points is clustered and not distributed uniformly in the space defined by the objective function values. There are two clusters near the end points of the Pareto frontier approximation and one more cluster close to the bottom right end of that frontier approximation. The fitness method used (Section 2.2.3) does tend to emphasise points near the ends of the frontier [Fraga and Amusat 2016] for multi-objective problems so these clusters were expected. Nevertheless, it is interesting to note that the infeasible points in the population are not clustered. This gives some confidence that there is sufficient diversity in the population even after 500 thousand function evaluations.
Figure 1: Outcome, in terms of the hyper-volume measure, of all the runs for the PPA solving the chlorobenzene process design problem with multiple objectives.
The behaviour of the PPA is affected by the values of the parameters, primarily the populaton size, \(n_p\), but less so by the maximum number of runners, \(n_{r,\max}\). Figure 1 shows the hyper-volume measure of the set of non-dominated points in the final population as a function of the population size, \(n_p\), and the maximum number of runners, \(n_{r,\max}\). The results are more consistent, i.e. tightly grouped, for the higher population cases.
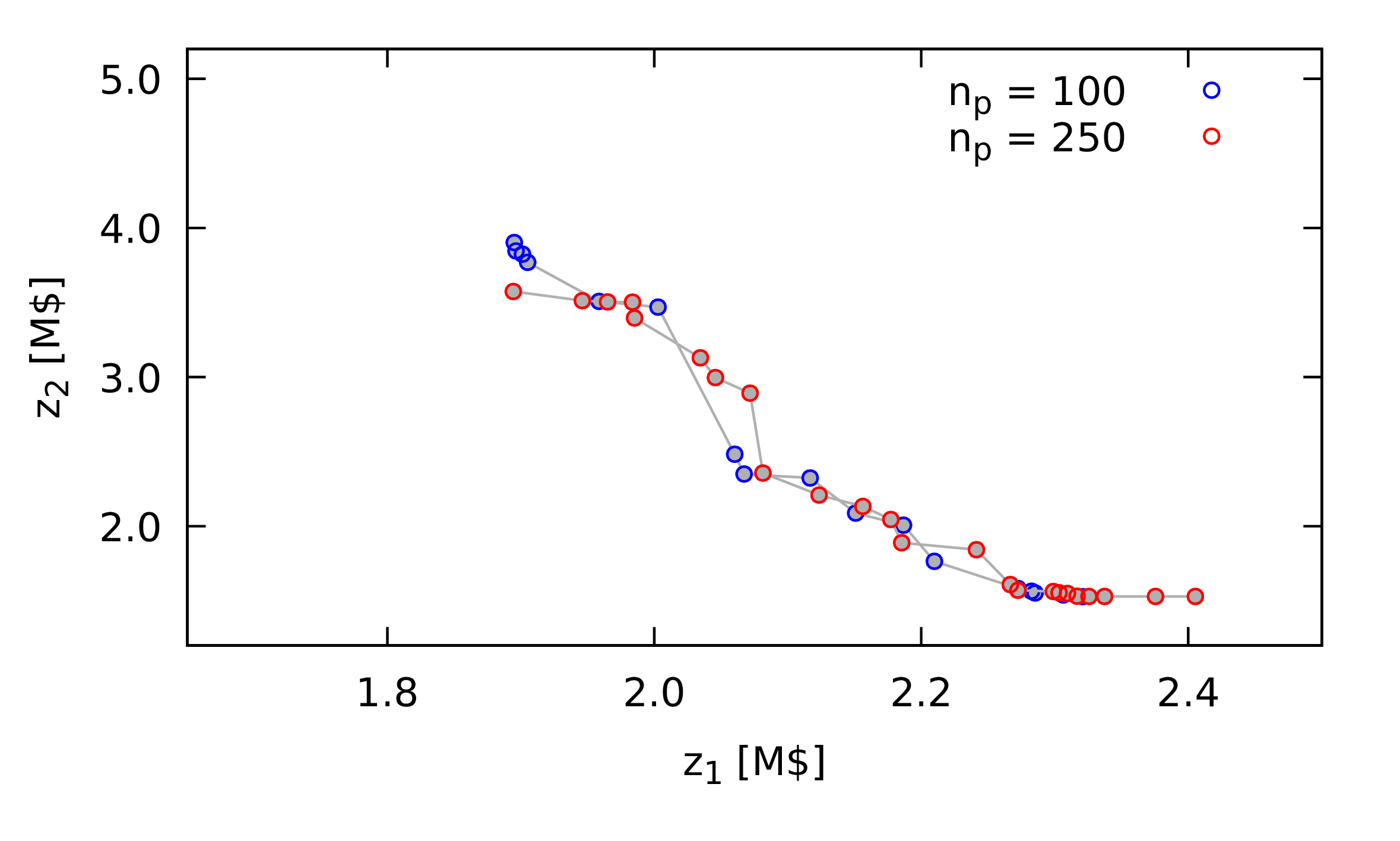
Figure 1: Comparison of sets of non-dominated points obtained with \(n_p=100\) (blue circles) and \(n_p=250\) (red circles) when solving the chlorobenzene process design multi-objective optimization problem.
The expectation is that the size of the population will affect the density of points in the approximation obtained. The number of function evaluations does not lead to an appreciable difference in hyper-volume outcome although it may have an outcome in terms of how well approximated the Pareto frontier may be throughout its length. This can be seen in Figure 1 which shows the sets of non-dominated points obtained with different population sizes. The set with \(n_p=100\) was also presented in Figure 1. The set obtained with \(n_p=250\) is super-imposed. The approximation to the Pareto frontier is better represented throughout and is also further extended at the bottom right end. The hyper-volume measure for the latter is 0.0812, slightly higher than the 0.0784 obtained with \(n_p=100\). In this case, this measure of quality seems consistent with our perception of what is a better outcome but, nevertheless, the measure should only be treated as a guide towards the quality of the solution obtained.
3.7. Summary
The design of a process using simulation software for the evaluation of alternative designs poses a challenge for gradient based optimization methods. Nature inspired optimization methods, however, are well suited to this problem. The application of the three nature inspired optimization methods to this problem has illustrated the ability of these methods to handle infeasible designs, evolving to feasible solutions quickly. The GA and PPA, in particular, appear to obtain good results with a reasonable computational effort. The PSO does appear to converge quickly to a good solution but then fails to evolve further.
4. Plug flow reactor
4.1. Introduction
Some process designs require identifying a distributed quantity, i.e. one which varies in either space or in time. An example of this is a plug flow reactor (PFR) in a fixed bed with catalyst distributed along the bed. The catalyst improves or, in some cases, enables the desired reactions. An example [exercise 2, Vassiliadis et al. 2021:311] of the design of a PFR with a catalyst is used to illustrate problems with distributed quantities.
The aim is to maximise the yield of the third species, the product of reactions involving 2 other species, with the feed consisting of the first species alone. The amount of catalyst along the bed of the reactor is \(u(x)\) and the reactor is 2 units of length long. The design problem is to identify \(u(x)\) for \(x \in [0.0,2.0]\) which maximises this yield:
\begin{equation} \label{orgb479460} \max_{u(x)} z = y_3(2.0) \end{equation}where the right hand side is the molar composition of the third species at the end of the reactor. The value of \(y_3\) is obtained by solving differential and algebraic equations. These equations describe the behaviour of the three species, \(y_i, \, i=1,2,3\) as a function of the distance, \(x\), along the reactor
\begin{align} \label{orge7c096d} \frac{\text{d}}{\text{d}x} y_1 &= u \left ( 15 y_2 - y_1 \right) \\ \frac{\text{d}}{\text{d}x} y_2 &= u \left ( y_1 - 15 y_2 \right ) - \left ( 2 - u \right ) y_2 \nonumber \\ y_3 &= 1 - y_1 - y_2 \nonumber \end{align}with initial conditions
\begin{align*} y_1(0) &= 1.0 \\ y_2(0) &= 0.0 \end{align*}and constraints and bounds
\begin{align*} 0 \le u(x) \le 1.0 \\ 0 \le x \le 2.0 \end{align*}4.2. The formulation for optimization
As discussed in Section 1.6, the choices of both formulation and representation for the design variables may have an impact on the performance of the optimization method and the resulting outcome. The first decision for this particular case study is how to formulate the continuous distribution of the catalyst over the length of the reactor.
The most straightforward formulation may be to discretise the spatial domain into a number of intervals and specify a step function with a specified constant catalyst amount for each interval in the spatial domain. Another straightforward alternative would be a linear function for the catalyst amount in each interval with the amounts matching at the end-points. The latter is a piece-wise linear formulation. A further alternative would be to define more complex functions, either for each of the intervals or over the full domain, functions which could have desirable continuity and smoothness properties.
A more complex function representation was used in [Rodman et al. 2018] for describing a time varying quantity (the operating temperature). The use of a continuous formulation with smoothness conditions was chosesn as being appealing to process operators, those charged with implementing the operating conditions identified by the solution of the operating design problem. A combination of spline functions for the operating temperature of the fermentation reactor was used to describe the continuous design variable. The same motivation may apply to the design of the PFR as well.
For the purpose of illustration, I will present first a step function to describe amount of catalyst as a function of spatial position, \(x\). Define \(n_x\) intervals over the full the spatial domain, \(x \in [0, 2]\): \[I_i = [x_{i}, x_{i+1}], \qquad i=1,\ldots,n_x \] with \(x_1=0\) and \(x_{n_x} = 2\). For each interval, a constant amount of catalyst, \(u_i\), will be present. Therefore, the decision variables for this optimization problem are the catalyst amounts in the \(n_x\) intervals, \(u_i\), and the intermediate points defining the intervals, \(x_i\), for \(i=2,\ldots,n_x-1\).
4.3. The representation
The first element to represent is the set of interior points defining the intervals. The simplest would be a uniform discretisation. A uniform discretisation leads to the need for a large number of intervals to enable sufficiently fine granularity to capture changes in the distributed quantity. A large number of intervals implies a large number of values for the distributed quantity to be represented. This can affect the computational efficiency but, more importantly, it will reduce the effectiveness of the optimization methods by increasing the dimension of the search space. Therefore, it may be advantageous to consider an adaptive placement of the points; see [Rodman et al. 2018] for an example of an adaptive representation.
Again, for clarity of exposition, I will present a uniform discretization first, specified by \(n_x\) implicitly: \( x_i = (i-1) \delta x\) for \(i \in 1,\ldots,n_x\) and \(\delta x = \frac{2}{n_x}\). For this discretisation, what remains is to find values of \(u_i \in [0,1]\); these will be the decision variables for the optimization problem.
4.4. Implementation
4.4.1. The model
The original set of differential-algebraic equations, eq. \eqref{orge7c096d}, is first converted into a system of ordinary differential equations by differentiating the algebraic equation:
\begin{align*} \frac{\text{d}}{\text{d}x} y_1 &= u \left ( 15 y_2 - y_1 \right) \\ \frac{\text{d}}{\text{d}x} y_2 &= u \left ( y_1 - 15 y_2 \right ) - \left ( 2 - u \right ) y_2 \\ \frac{\text{d}}{\text{d}x} y_3 &= - \frac{\text{d}}{\text{d}x} y_1 - \frac{\text{d}}{\text{d}x} y_2 \end{align*}which together with the extra initial condition \[ y_3(0) = 0 \] defines an initial value ODE problem. This is easier to solve than the original system of differential-algebraic equations.
The DifferentialEquations.jl Julia package [Rackauckas and Nie 2017] is used to solve the ODE problem. The problem is defined by using ODEProblem from that package, passing it the same of a function, f, that implements the system of differential equations with the following form:
\[ \frac{\text{d}}{\text{d}x} y(x) = f(y, p, x) \]
where \(y\) are the unknowns as functions of the spatial dimension, \(x\), and \(p\) is some problem specific set of parameters. For this problem, \(p\) will be used to pass the catalyst amount.
As the catalyst amount is represented by a step function, the solver will be applied to each interval in turn. Doing so has two advantages:
- the differential equation solver will not need to handle discontinuities or non-smooth behaviour, enabling the use of larger time steps within each interval, and
- the implementation of the function describing the right hand side of the differential equations will only need a single value to represent the catalyst amount.
Therefore, the right hand side function is
1:function reactor(y, u :: Real, x)2:dy = [ u * (15*y[2] - y[1])3:u * (y[1]-15*y[2])-(2-u)*y[2]]4:[ dy[1]5:dy[2]6:-dy[1]-dy[2]]7:end
It will become clear, below, why the second argument, u, has been explicitly typed to be a single real number.
The ODE problem defined by the reactor function can now be solved using the solve function from the DifferentialEquations.jl package, simulating the behaviour of the reactor. The solve function returns a full profile of the simulation. This profile can subsequently be used to define an objective function for the design problem.
1:using DifferentialEquations2:function simulate(u)3:y = [1.0, 0.0, 0.0] # initial conditions4:profile = [y]5:nx = length(u)6:δx = 2/nx7:for i ∈ 1:nx8:xspan = ((i-1)*δx, i*δx)9:prob = ODEProblem(reactor, y, xspan, u[i])10:ret = DifferentialEquations.solve(prob)11:y = ret.u[end]12:push!(profile, y)13:end14:# return last result and the full profile15:(y, profile)16:end
In the code, the following lines are worth noting:
- Each interval in the domain is considered in turn.
- Each interval defines a new
ODEProblem. - And each such ODE problem is solved
- The values of the unknown variables,
y, at the end of each interval are extracted from the data structure returned bysolve… - … and collected into
profilefor later use or analysis. - The function returns the final values of the unknown variables as well as an array of values for those variables for all the intervals in the full domain.
This code can be tested by evaluating a randomly generated catalyst distribution for a given discretization:
1:using NatureInspiredOptimization: printvector2:using NatureInspiredOptimization.PFR: simulate3:using Plots4:# create a random catalyst vector5:n = 106:u = rand(n)7:# simulate the reactor8:solution, profile = simulate(u)9:# output and plot the solution10:printvector("Solution: ", solution, "")11:δx = 2.0/n # size of each interval12:# end points of intervals13:x = [i*δx for i ∈ 0:n]14:# profile includes values for each species15:np = length(profile) # should be n+1...16:p = plot(x, [profile[j][1] for j ∈ 1:np])17:plot!(p, x, [profile[j][2] for j ∈ 1:np])18:plot!(p, x, [profile[j][3] for j ∈ 1:np])19:# create vectors for step function plot20:# of the catalyst amount21:x = [0.0]22:v = [u[1]]23:for i=1:n-124:push!(x, i*δx)25:push!(v, u[i])26:push!(x, i*δx)27:push!(v, u[i+1])28:end29:push!(x, 2.0)30:push!(v, u[end])31:plot!(p, x, v, label="U")32:savefig("images/pfrsimulationtest.png")
Figure 1: Profiles of the spatial dependent variables for the PFR case study, including both the dependent variables and the design variable, the amount of catalyst to deposit along the reaction. This catalyst amount varies from step to step, resulting in a rather messy profile.
This code also uses the Plots Julia package which provides a large number of plotting related functions.3 Lines 13 to 31 plot out each of the individual species profiles as well as the catalyst amount, as a function of position in the reactor, x. Figure 1 shows the result of the plot statements. Note that the actual output will be different each time this code is evaluated due to the use of rand in line 6.
4.4.2. The optimization problem
Given the implementation of the model and the ability to simulate the behaviour of the reactor for different feed rates, we can now define the first objective function for use with the optimization methods:
1:function f(u)2:# simulate the reactor with this rate3:solution, profile = simulate(u)4:# the objective is to maximise the production of P5:z = - solution[3] # yield of y[3]6:(z, 0.0) # always feasible7:end
The simulation returns, as we have seen, the final values of the dependent variables. For optimization, the value of interest is the third species. As all of the optimization methods have been implemented to minimise the objective function, the value returned is the negative of the composition, line 5, so that minimization of this negative value corresponds to maximization of the final composition. Note also that the simulation should always be successful and so all designs considered will be feasible.
4.4.3. Results
4.4.3.1. Genetic algorithm
The genetic algorithm will be applied considering a small initial population, consisting of the lower and upper bounds on all variables (i.e. the catalyst amounts), and the mid-point between those bounds. Different numbers of intervals for discretization are considered and the population size is four times the number of intervals. No parameter tuning is considered here; the defaults implemented in the code are used for everything but the population size.
1:using NatureInspiredOptimization: Point, printvector2:using NatureInspiredOptimization.PFR: f3:using NatureInspiredOptimization.GA: ga4:for n ∈ [5 10 20 50]5:lower = zeros(n) # U ≥ 0.06:upper = ones(n) # U ≤ 1.07:p0 = [ Point(lower, f)8:Point(lower + (upper-lower)/2.0, f)9:Point(upper, f) ]10:for run ∈ 1:1011:starttime = time()12:best, p, ϕ = ga(13:p0,14:f,15:lower = lower,16:np = 4*n,17:upper = upper,18:)19:deltatime = time() - starttime20:printvector("| best: |", best.x, "| ")21:println("\nfinal: $run $n $deltatime $(best.z) $(best.g))")22:end23:end
Figure 1: Box plot of outcomes obtained using the genetic algorithm for the plug flow reactor design problem for different values of \(n_x\), the number of intervals for the spatial domain. The box plots show the mean, minimum, and maximum values as well as the lower and upper quartiles. Outliers are indicated with \(\times\) points.
Figure 1 shows the results obtained from solving the PFR design problem 10 times for each value of \(n_x\), the number of intervals to use in the discretization of the spatial domain. The results show that the outcome, in terms of the objective function value obtained, improve with the increase in the number of intervals. Interestingly, the variation in final outcome also seems to improve with increased number of discrete intervals.
4.4.3.2. Particle swarm optimization
As with the genetic algorithm, default parameters values are used except for the population size. The same sizes are considered here as done for the genetic algorithm. The initial population is the same although the method itself will ensure the population is expanded to the right size using randomly generated solutions in the domain.
1:using NatureInspiredOptimization: Point, printvector2:using NatureInspiredOptimization.PFR: f3:using NatureInspiredOptimization.PSO: pso4:for n ∈ [5 10 20 50]5:lower = zeros(n) # U ≥ 0.06:upper = ones(n) # U ≤ 1.07:p0 = [ Point(lower, f)8:Point(lower + (upper-lower)/2.0, f)9:Point(upper, f) ]10:for run ∈ 1:1011:starttime = time()12:best, p = pso(13:p0,14:f,15:lower = lower,16:np = 4*n,17:upper = upper,18:)19:deltatime = time() - starttime20:printvector("| best: |", best.x, "| ")21:println("\nfinal: $run $n $deltatime $(best.z) $(best.g))")22:end23:end
Figure 1: Box plot of outcomes obtained using the particle swarm optimization method for the plug flow reactor design problem for different values of \(n_x\), the number of intervals for the spatial domain. The box plots show the mean, minimum, and maximum values as well as the lower and upper quartiles. Outliers are indicated with \(\times\) points.
Figure 1 shows the results obtained from solving the PFR design problem 10 times for each value of \(n_x\), the number of intervals to use in the discretization of the spatial domain. The results show that the outcome, in terms of the mean objective function value obtained, improve with the increase in the number of intervals. However, there is significant spread in final outcomes except for the case with \(n_x=5\).
4.4.3.3. Plant propagation algorithm
Again, the default values for the parameters are used, including, in this case, the population size. The initial population consists solely of the mid-point design. The plant propagation algorithm has been found to work well even when started with a single point.
1:using NatureInspiredOptimization: Point, printvector2:using NatureInspiredOptimization.PFR: f3:using NatureInspiredOptimization.PPA: ppa4:for n ∈ [5 10 20 50]5:lower = zeros(n) # U ≥ 0.06:upper = ones(n) # U ≤ 1.07:p0 = [Point(lower + (upper-lower)/2.0, f)]8:for run ∈ 1:109:starttime = time()10:best, p, ϕ = ppa(11:p0,12:f,13:lower = lower,14:upper = upper,15:)16:deltatime = time() - starttime17:printvector("| best: |", best.x, "| ")18:println("\nfinal: $run $n $deltatime $(best.z) $(best.g))")19:end20:end
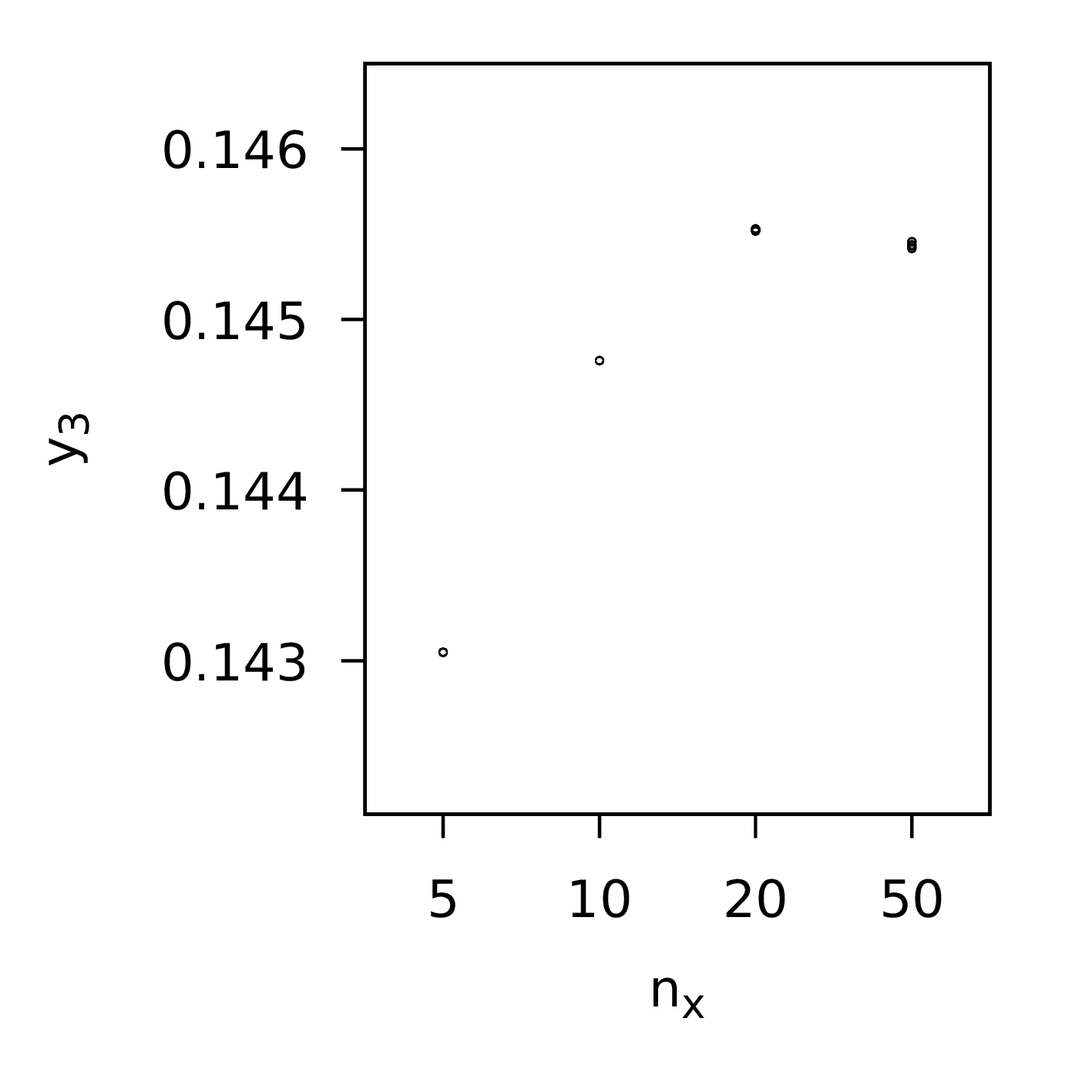
Figure 1: Results obtained using the plant propagation algorithm for the plug flow reactor design problem. Ten attempts with each value of the number of intervals for the \(x\) domain, \(n_x\), are plotted.
The results are summarised in Figure 1. For each value of the number of discrete intervals to use along the spatial dimension, i.e. along the reactor, \(n_x\), the result for ten runs are shown. A scatter plot, instead of a box plot, is used in this case due to the very small differences in outcomes obtained for each case. More specifically, for \(n_x=5\) and \(n_x=10\), all the runs obtain the same outcome. For \(n_x=20\), some variation can be seen in the outcome and this is more evident for \(n_x=50\). Interestingly, the results with \(n_x=20\) are better than those with 50; this is likely due to needing more iterations to search the bigger search space due to the large number of decision variables.
More intervals are needed to capture the level of detail that may be needed to achieve the best outcome. However, this increase leads to a concomitant increase in the dimension of the search domain, making the search harder. This motivates the desire to consider a different representation of solutions, one that may have less of an impact on the search but which captures solutions of interest.
4.5. Alternative representation
The results using the discrete step representation, see Figure 1, are designs that an engineer may consider uninteresting or even not realistic for actually building the reactor. Such almost erratic changes in the amount of catalyst to place along the reactor may not be appealing. A similar comment was made, by Rodman et al. [Rodman et al. 2018], when discussing results obtained with a similar discrete representation for the operating temperature of a fermentation unit in brewing. The suggestion in that work was to use a representation for the optimization procedure that is guaranteed to lead to more pleasing outcomes in terms of the actual design.
In this section, I present a similar approach, one which illustrates the use of multiple dispatch in Julia. The challenge is to find a representation that describes designs with desirable attributes. The main desirable attribute would be more gradual changes in the amount of catalyst on the bed of the reactor. Therefore, a representation that is based on a continuous and smooth function would satisfy this desire.
Figure 1: Example profile and catalyst amount for the fed batch plug flow reactor design, obtained with \(n_x=5\) discrete intervals for the spatial dimension.
The results obtained by the various methods for larger numbers of intervals tend to have a similar shape: a high value at the start, a plateau along the length of most of the reactor, and then no catalyst for the last part of the reactor would seem to be the aim. However, it is useful to look at the results obtained, with the PPA, for \(n_x=5\), where all the attempts return designs such as that shown in Figure 1. This shows a slight increase in the amount of the catalyst in the plateau region.
Figure 1: The plot of \(a(x) = \frac{\frac{\pi}{2} - \arctan(10 (2 x-1))}{\pi}\) function over the [0,20] domain.
Consider the function illustrated in Figure 1:
\begin{equation} \label{org1dbf1db} a(x) = \frac{\frac{\pi}{2} - \arctan(10 \left ( 2 x - 1 \right ))}{\pi} \end{equation}for \(x \in [0:1]\). Picture two curves like this, each scaled in both dimensions, connected by a straight line. The result could be used to cover the space of designs where the shape of the resulting curve is similar to that observed in Figure 1. Other functions, such as Bezier curves, could be used to represent the possible designs.
The advantage of using a function to represent potential solutions to the design problem is that these solutions will exhibit not only a particular shape but will be continuous over the whole spatial domain and also smooth everywhere except at the two connection points.
To stretch and place the curves, we parameterise the \(a(x)\) function,
\begin{equation} a(x,\beta) = \frac{\frac{\pi}{2} - \arctan(\beta \left ( 2 x - 1 \right ))}{\pi} \end{equation}by replacing the 10 in the version used for illustration with α. This parameter changes the steepness of the curve. Then we can scale and shift this function by
\begin{equation} f(x) = \alpha a(x, \beta) + \gamma \end{equation}We want \(f(x) \in [0,1]\) for all values of α, β, and γ. β does not change the range of \(a\); if we restrict α ∈ [0,1], the product is ∈ (0,1). The amount of shifting will depend on α: \(\gamma \in [0,1-\alpha]\). This combination of bounds on these parameters will ensure that the result is suitable for a representation of \(u(x)\) for the reactor design model.
To create the composite function which includes a first component based on \(a(x)\), a connecting line, and then the second case of \(a(x)\), we have to shrink and position the curves appropriately. We define two interior points \(x_1\) and \(x_2\) and then defined the three components as follows, to give a value of \(u \in [0,1]\) for all \(x \in [0,2]\):
\begin{equation} \label{org5d5933d} u(x) = \left \{ \begin{array}{ll} f_1(\frac{x}{x_1}) & x \le x_1 \\ f_1(1) + \frac{f_2(0)-f_1(1)} {x_2-x_1} (x-x_1) & x_1 < x < x_2 \\ f_2(\frac{x-x_2}{2-x_2}) & x \ge x_2 \end{array} \right . \end{equation}where \(f_1\) and \(f_2\) are the same as \(f(x)\) with their own values of α, β, and γ.
This representation of \(u(x)\) has 8 parameters in total, 3 for \(f_1(x)\), 3 for \(f_2(x)\), \(x_1\), and \(x_2\), all with bounds \([0,1]\). The advantage of this representation is that it provides a continuous function throughout the interval with a small number of parameters.
4.6. Implementation
Implementing this alternative representation requires the definition of a function to retrieve the value of \(u(x)\) for any \(x \in [0,2]\) and to be able to access this function from the function that implements the right hand side of equation \eqref{orge7c096d}. The code below uses Julia's multiple dispatch capabilities to implement this.
4.6.1. The representation
The first step is to define a structure which encodes the representation. Multiple dispatch will be able to differentiate by the type of data structure used to pass the design point to the simulation method and hence the evaluation of the right hand side of equation \eqref{orge7c096d}.
1:struct CatalystAmount2:α3:β4:γ5:x6:function CatalystAmount(r)7:new( [r[1], r[4]], # α8:[r[2], r[5]], # β9:[(1.0-r[1])*r[3], # γ₁10:(1.0-r[4])*r[6]], # γ₂11:[r[7], 2.0-r[8]] ) # x12:end13:end
The data structure makes use of a defined constructor (line 6) to assign the values from the 8 valued real vector to the individual parameters for the function defined above in equation \eqref{org5d5933d}. This latter equation is then implemented:
1:function a(x, β)2:(π/2 - atan(20*β*(2*x-1))) / π3:end4:function f₁(u, x)5:u.α[1] * a(x, u.β[1]) + u.γ[1]6:end7:function f₂(u, x)8:u.α[2] * a(x, u.β[2]) + u.γ[2]9:end
\(u(x)\) will be evaluated by using these functions. I will use operator overloading to allow us to use the u[x] array index syntax to evaluate \(u\) at any point \(x \in [0,2]\). This is done by defining the getindex function.
1:function Base.getindex(u :: CatalystAmount, x)2:if x ≤ u.x[1] && u.x[1] > eps()3:return f₁(u, x/u.x[1])4:elseif u.x[1] ≤ x ≤ u.x[2] && (u.x[2] - u.x[1]) > eps()5:return f₁(u, 1.0) + (f₂(u, 0.0) - f₁(u, 1.0))/(u.x[2]-u.x[1]) * (x - u.x[1])6:elseif u.x[2] ≤ x && u.x[2] < 2.07:return f₂(u, (x-u.x[2])/(2.0-u.x[2]))8:else9:error("$x not in bounds [0,2]")10:end11:end
Note that in line 9 the function will throw an error if we attempt to evaluate \(u\) outside the spatial domain defined.
The following code tests the new representation. It generates the graph shown in Figure 1:
1:using NatureInspiredOptimization.PFR: CatalystAmount2:using Plots3:r = 0.5*ones(8)4:r[6] = 0 # do not shift second atan5:@show u = CatalystAmount(r)6:plotx = [0.02*i for i ∈ 0:100]7:ploty = [u[x] for x ∈ plotx]8:plot(plotx,ploty, label="u(x)")9:savefig("images/pfrcatalystamountalternative.pdf")
Figure 1: Profile of catalyst amount using the alternative representation with values of 0.5 for all parameters except for γ2 = 0.0.
4.6.2. The model
The model is still a set of differential and algebraic equations. The implementation for the alternative representation differs solely in how the catalyst amount is represented. In the simple step representation, the amount is constant over a time interval. Now it varies continuously. An instance of the structure defined above is passed as an argument to the reactor model instead of a single value. The structure is evaluated at the particular point in the spatial dimension using the operator overloading of array indexing. The advantage of the latter is that the model equations mirror the mathematical representation.
1:function reactor(y, u :: CatalystAmount, x)2:dy = [ u[x] * (15*y[2] - y[1])3:u[x] * (y[1]-15*y[2])-(2-u[x])*y[2]]4:[ dy[1]5:dy[2]6:-dy[1]-dy[2]]7:end
Note that by specifying the type of the second argument, Julia will use this version automatically when the catalyst amount is specified as an instance of CatalystAmount instead of simply a vector of real values.
This model is then used in the alternative simulate function, again making use of multiple dispatch to invoke this function:
1:using DifferentialEquations2:function simulate(u :: CatalystAmount)3:y = [1.0, 0.0, 0.0] # initial conditions4:profile = [y]5:intervals = [(0.0, u.x[1])6:(u.x[1], u.x[2])7:(u.x[2], 2.0)]8:for xspan ∈ intervals9:if xspan[2] - xspan[1] > eps()10:prob = ODEProblem(reactor, y, xspan, u)11:ret = DifferentialEquations.solve(prob)12:y = ret.u[end]13:profile = vcat(profile, ret.u)14:end15:end16:(y, profile) # result and full profile17:end
As in the step function representation, the simulation solves the system of differential equations in a sset of intervals, sequentially. Lines 5-7 defined three intervals: the first which has an arc tan function representation, the second being the straight line connecting the first and third functions, and the third also using an arc tan function. Then lines 8 through 14 solve the differential equations in each interval.
4.6.3. The optimization problem
Given the implementation of the alternative representation, an alternative objective function is implemented that takes the decision variables, creates an instance of the data structure defined above, and simulates the reaction. The value of the objective function is again the negative of the final composition of the third species and again all design points (within the search domain) are feasible.
1:function altf(u :: Vector{Float64})2:# simulate the reactor with this rate3:solution, profile = simulate(CatalystAmount(u))4:# the objective is to maximise the production of P5:z = - solution[3] # yield of y[3]6:(z, 0.0) # always feasible7:end
4.6.4. Results
4.6.4.1. Genetic algorithm
The code to solve this problem, with the alternative representation, is identical to that used with the first representation except for lines 2 and 15 where the new objective function, altf, is specified.
1:using NatureInspiredOptimization: Point, printvector2:using NatureInspiredOptimization.PFR: CatalystAmount, altf3:using NatureInspiredOptimization.GA: ga4:n = 8 # size of u description5:lower = zeros(n)6:upper = ones(n)7:p0 = [ Point(lower, altf)8:Point(lower + (upper-lower)/2.0, altf)9:Point(upper, altf) ]10:@show p011:for run ∈ 1:1012:starttime = time()13:best, p, ϕ = ga(14:p0,15:altf,16:lower = lower,17:np = 4*n,18:upper = upper,19:)20:deltatime = time() - starttime21:printvector("| best: |", best.x, "| ")22:println("\nfinal: $run $deltatime $(best.z) $(best.g))")23:end
Figure 1: Box plot of outcomes obtained using the genetic algorithm for the plug flow reactor design problem with the alternative representation. For computational comparison, the population size is 32, corresponding to 4 times the number of optimization variables. The box plots show the mean, minimum, and maximum values as well as the lower and upper quartiles. Outliers, if any, are indicated with \(+\) points.
Figure 1 shows the results obtained from solving the PFR design problem 10 times using this alternative representation. The population size is 32, based on 4 times the number of values in the representation, which allows us to comment not only on the quality but the relative computational performance. The results compared favourably with \(n_x=20\) with the original representation but require approximately 40% of the computational effort.
4.6.4.2. Particle swarm optimization
For the particle swarm method, again the only differences (lines 2 and 15) are due to the objective function used in this case.
1:using NatureInspiredOptimization: Point, printvector2:using NatureInspiredOptimization.PFR: altf3:using NatureInspiredOptimization.PSO: pso4:n = 8 # size of u description5:lower = zeros(n)6:upper = ones(n)7:p0 = [ Point(lower, altf)8:Point(lower + (upper-lower)/2.0, altf)9:Point(upper, altf) ]10:@show p011:for run ∈ 1:1012:starttime = time()13:best, p = pso(14:p0,15:altf,16:lower = lower,17:np = 4*n,18:upper = upper,19:)20:deltatime = time() - starttime21:printvector("| best: |", best.x, "| ")22:println("\nfinal: $run $deltatime $(best.z) $(best.g))")23:end
Figure 1: Box plot of outcomes obtained using the particle swarm optimization method for the plug flow reactor design problem for different values of \(n_x\), the number of intervals for the spatial domain. The box plots show the mean, minimum, and maximum values as well as the lower and upper quartiles. Outliers are indicated with \(+\) points.
Figure 1 shows the results obtained from solving the PFR design problem 10 times. This time, the quality of solution obtained is similar to that obtained with \(n_x=50\) with the original representation, although with a few more outliers. The computational effort is less than 20%, moreover.
4.6.4.3. Plant propagation algorithm
Finally, for this method, again the main differences are in lines 2 and 15 for the objective function used but I have also initialised the population to include the lower and upper bounds, for a more fair comparison with the other methods.
1:using NatureInspiredOptimization: Point, printvector2:using NatureInspiredOptimization.PFR: altf3:using NatureInspiredOptimization.PPA: ppa4:n = 8 # size of u description5:lower = zeros(n)6:upper = ones(n)7:p0 = [ Point(lower, altf)8:Point(lower + (upper-lower)/2.0, altf)9:Point(upper, altf) ]10:@show p011:for run ∈ 1:1012:starttime = time()13:best, p, ϕ = ppa(14:p0,15:altf,16:lower = lower,17:upper = upper,18:)19:deltatime = time() - starttime20:printvector("| best: |", best.x, "| ")21:println("\nfinal: $run $deltatime $(best.z) $(best.g))")22:end
Figure 1: Results obtained using the plant propagation algorithm for the plug flow reactor design problem with the alternative representation. All ten attempts obtain very similar results. A scatter plot has been used instead of a box plot due to this lack of variation in outcome.
The results for the plant propagation algorithm with the alternative representation are summarised in Figure 1. Again, in this case, a scatter plot is used as there is insufficient variation in the outcomes to fruitfully use a box whisker diagram. All the attempts return essentially the same objective function value. This value is similar to that obtained with the step function representation using 20 intervals but with 40% of the computational effort and better than that obtained with 50 intervals with less than 20% of the computation.
4.6.5. Discussion
The outcome of optimization based design that is most important is not the objective function value but the actual design generated. The question addressed implicitly in this section is whether a given representation generates good designs. The step function representation is not ideal (cf. Figure 1) and the intention of the alternative representation is to have more appealing designs.
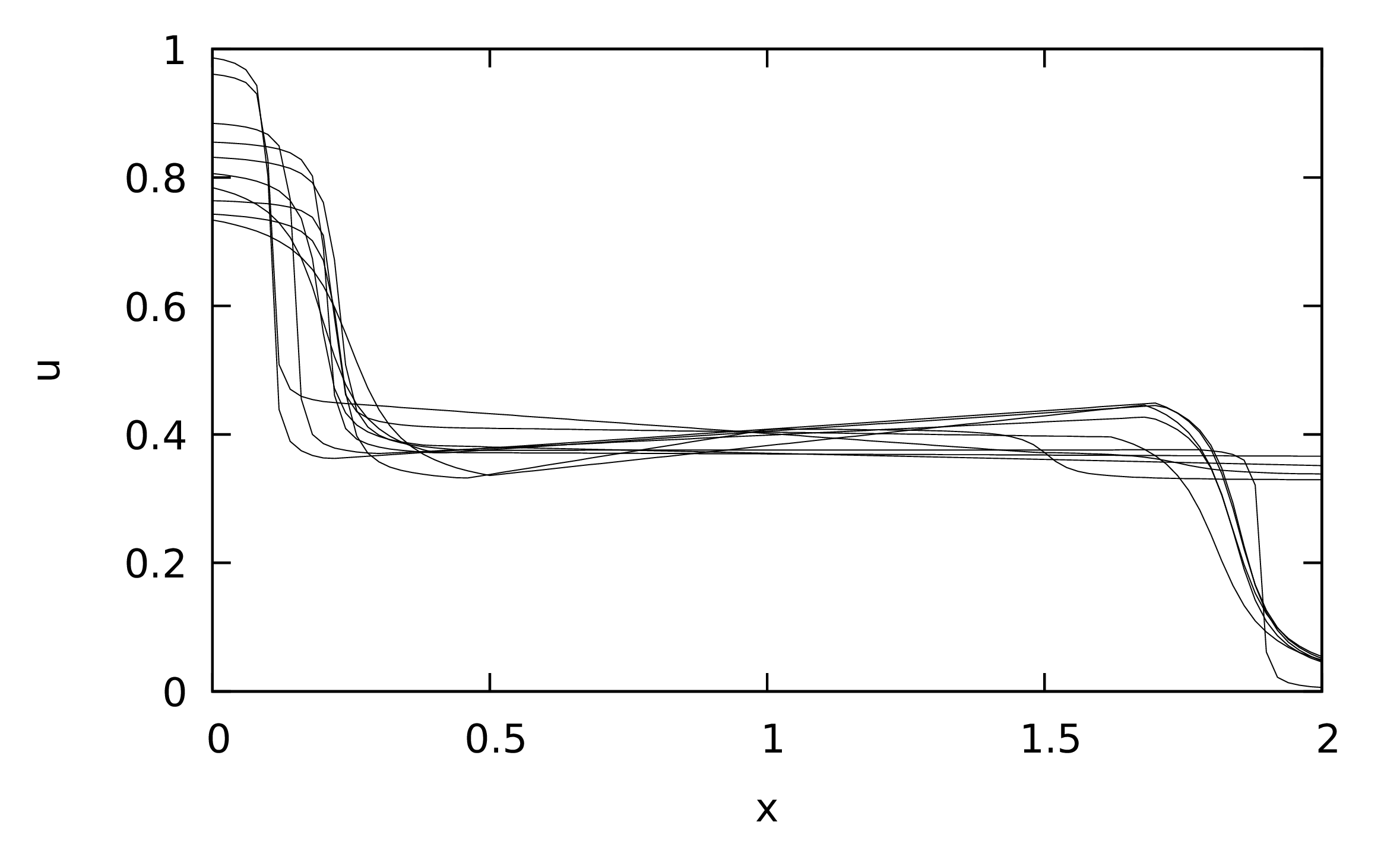
Figure 1: Catalyst amount profiles for the best design obtained in each of the runs with the GA method.
Figure 1: Catalyst amount profiles for the best design obtained in each of the 10 runs with the PSO method.
Figure 1: Catalyst amount profiles for the best design obtained in each of the 10 runs with the PPA method.
Figures 1, 1, and 1 show the outcome of the 10 runs for each of the three optimization methods: GA, PSO, and PPA. Each graph presents the catalyst amount as a function of the spatial dimension. The different figures illustrate how the various methods perform, in terms of consistency of outcome. The GA generates solutions that are all qualitatively similar. The PSO method solutions exhibit differences in the shape. Finally, the PPA outcome is essentially the same in each run. These qualitative differences in the outcomes of the three methods are expected given the differences in the values of the objective function obtained.
Figure 1: Catalyst amount profiles for 10 runs using the GA method but with nfmax set to 105 instead of the default 104.
For the genetic algorithm, we have also solved the problem 10 times using 10 times as many function evaluations, nfmax set to 105 instead of the default 104. The outcomes are shown graphically in Figure 1. The convergence to a single profile has improved although there is still more deviation in the outcomes than exhibited by the plant propagation algorithm, Figure 1.
In any case, other than a number of the designs obtained with the particle swarm optimization method, the profiles have shapes which are more appealing to a design engineer. They are smooth and have clearly identified regions which constant behaviour. It is expected that these profiles could be implemented in the actual plug flow reactor.
5. Heat exchanger networks
The third case study illustrates the use of more complex data structures in optimization. Although the design variables will be represented, again, by a vector of real numbers, the evaluation of each design will require traversing a complex graph structure. The aim of this section therefore is to illustrate complex modelling that may not be straightforward expressed as a set of equations as typically desired for mathematical programming methods.
5.1. Heat exchanger networks
Process integration, where excess heat in one part of a process is used to meet heating demands in another part, has a long history due to the potential to save significant costs by reducing the amount of external utilities used for heating and for cooling. Heat is transferred between processing steps in a process through a heat exchanger network. A good review of this topic can be found in Chapter 3 of [Towler and Sinnott 2013].
Identifying the best such network is a challenging optimization problem. This problem has been the focus of research in optimization methods and modelling for a long time [Fraga et al. 2001b; Zamora and Grossmann 1998; Morton 2002; Floudas et al. 1986; Linnhoff and Hindmarsh 1983; Linhoff and Flower 1978]. The problem is typically formulated as a mixed integer nonlinear programme (MINLP) representing a superstructure of all the possible structures or networks.
In this chapter, I will present a graph theoretic approach to modelling heat exchanger networks. This approach will use only real valued decision variables and will therefore be suitable for solution using the three nature inspired optimization methods as presented and implemented in this book. This problem is significantly more complex than the previous two and involves the following:
- definition of data structures for the various aspects of heat exchange network designs;
- the representation of the superstructure, a directed graph which represents the set of potential structures to be considered by the search procedures; and,
- the evaluation of a specific network design, requiring traversal of a complex graph and evaluation of the individual units.
Associated with the above is a simple visualization function for presenting solutions to the heat exchanger network design problem.
5.1.1. Example problem
| ID | Stream | \(\dot{m}C_p\) | \(T_{\text{in}}\) | \(T_{\text{out}}\) | \(h\) |
|---|---|---|---|---|---|
| \(\frac{\text{kW}}{\,^\circ\text{C}}\) | \(\,^\circ\text{C}\) | \(\,^\circ\text{C}\) | \(\frac{\text{kW}}{\text{m}^2\text{K}}\) | ||
| 1 | H1 | 1 | 400 | 120 | 2.0 |
| 2 | H2 | 2 | 340 | 120 | 2.0 |
| 3 | C1 | 1.5 | 160 | 400 | 2.0 |
| 4 | C2 | 1.3 | 100 | 250 | 2.0 |
| Steam | 500 | 500 | 1.0 | ||
| Water | 20 | 30 | 1.0 |
Table 1 [Example 16.1, Biegler et al. 1997:529] presents the problem table for the definition of a heat exchanger network design problem. The problem definition consists of the streams that require cooling (hot streams, labelled H1 and H2) and heating (cold streams, labelled C1 and C2). The external utilities available are also specified: steam for heating and liquid water for cooling. The design or optimization problem requires the following information in order to estimate costs and impose some constraints on the design: a minimum heat recovery approach temperature (HRAT) of 10 \(\,^\circ\text{C}\), cost of steam at 80 currency units (cu) per kWyr (i.e. the annual cost of providing a kW continually for a year), cost of cooling water at 20 cu per kWyr, cost of each exchanger using \[ c = 6600 + 670 A ^ {0.83} \] all from Biegler et al. [Biegler et al. 1997:16].
The area for the heat exchanger, \(A\) [m2], is estimated using \[ Q = UA\Delta T_{\text{LMTD}} \] where \(Q\) is the actual rate of heat exchanged. LMTD is the log mean temperature difference, the driving force for the heat exchange, \[ \Delta T_{\text{LMTD}} = \frac{\Delta T_1 - \Delta T_2}{\ln \frac{\Delta T_1}{\Delta T_2}} \] where
\begin{align*} \Delta T_1 &= T_{H,\text{out}} - T_{C,\text{in}} \\ \Delta T_2 &= T_{H,\text{in}} - T_{C,\text{out}} \end{align*}assuming counter-current operation. To avoid computational issues arising when \(\Delta T_1 = \Delta T_2\), \(\Delta T_{\text{LMTD}}\) is approximated using the following approximation [Chen 1987]: \[ \Delta T_{\text{LMTD}} \approx \left ( \Delta T_1 \Delta T_2 \frac {\Delta T_1 + \Delta T_2} {2} \right )^{\frac{1}{3}} \] \(U\) is the overall heat transfer coefficient, \[ \frac{1}{U} = \frac{1}{h_i} + \frac{1}{h_j}\] for exchange between two streams, \(i\) and \(j\), which may be process streams or external utilities.
5.1.2. Data structures
Representing the problem and aspects of the solution will make use of some specific data structures for process streams, utilities, and heat exchangers.
5.1.2.1. Stream
The problem table, e.g. 1, consists of a number of hot and cold process streams. These are represented in Julia with the following type:
1:mutable struct Stream2:name # descriptive3:type # :hot or :cold4:mcp # W or kW / K5:Tin # K or C6:Tout # K or C7:h # W or kW / K / m^28:Q # W or kW typically9:end
The type, line 3, will be given a value of :hot or :cold. The : is the quote operator in Julia and its use in this manner is to create values of type Symbol. This makes code potentially easier to understand when compared with using, for instance, integer values to represent alternative cases.
On line 1, the modified mutable is used to indicate that instances of this type will be modifiable after creation. By default, Julia creates instances of types that cannot be changed after they are instantiated. However, when a heat exchanger network is evaluated (see Section 5.5 below), instances of this type will need to be updated as different amounts of exchange between hot and cold streams are considered.
For this structure, we define two constructors making it easier to create new Stream instances. The first defines a Stream based on the temperatures and heat capacity values, calculating the amount of heat to remove or obtain. The second creates a new Stream instance from an existing one.
1:# constructor which calculates Q2:Stream(name,type,mcp,Tin,Tout,h) =3:Stream(name, type, mcp,4:Tin, Tout, h,5:abs(mcp*(Tout-Tin)))6:# constructor which copies existing Stream instance7:Stream(s :: Stream) = Stream(s.name, s.type, s.mcp,8:s.Tin, s.Tout, s.h, s.Q)
We also define some functions to make output clearer and to support easy checking of the type of stream:
1:# informative output2:Base.show(io :: IO, s :: Stream) = print(io, "$(s.name): $(s.Tin) → $(s.Q)$(s.type == :hot ? "↓" : "↑") → $(s.Tout)")3:# predicates4:iscold(s :: Stream) = s.type == :cold5:ishot(s :: Stream) = s.type == :hot
We can test the above functions by defining the streams for the problem table, Table 1:
1:using NatureInspiredOptimization.HEN: Stream2:streams = [Stream("h1", :hot, 1.0, 400, 120, 2.0)3:Stream("h2", :hot, 2.0, 340, 120, 2.0)4:Stream("c1", :cold, 1.5, 160, 400, 2.0)5:Stream("c2", :cold, 1.3, 100, 250, 2.0)]
The output of this code segment is
4-element Vector{Stream}:h1: 400.0 → 280.0↓ → 120.0h2: 340.0 → 440.0↓ → 120.0c1: 160.0 → 360.0↑ → 400.0c2: 100.0 → 195.0↑ → 250.0
5.1.2.2. External utility
A utility is essentially an external stream which will provide heat or remove heat and hence looks similar to the Stream structure but includes a cost model, a model which determines the cost of using this utility, in currency units, for the actual amount of heat required or removed:
1:struct ExternalUtility2:name3:type # hot or cold4:Tin5:Tout6:h7:model # f(Q)8:end9:ishot(u :: ExternalUtility) = u.type == :hot
The cost model will typically be specified using inline anonymous functions, such as Q -> 120*Q. The external utilities for the example in Table 1 are defined by
1:using NatureInspiredOptimization.HEN: ExternalUtility2:[ExternalUtility("steam", :hot,3:500.0, 500.0, 1.0,4:Q -> 120.0*Q)5:ExternalUtility("water", :cold,6:20.0, 30.0, 1.0,7:Q -> 20.0*Q)]
which outputs
2-element Vector{ExternalUtility}:ExternalUtility("steam", :hot, 500.0, 500.0, 1.0,var"#5#7"())ExternalUtility("water", :cold, 20.0, 30.0, 1.0,var"#6#8"())
The last argument in each external utility in the output is the reference to the anonymous functions used to calculate the operating cost of the utility consumed.
5.1.2.3. Infeasibility exception
The key processing step in a heat exchanger network is the heat exchanger. A heat exchanger transfers heat from a hot stream to a cold stream. Each stream has an inlet temperature and an outlet temperature which is a function of the amount of heat transferred. The code which defines the heat exchanger data structure is below. First, however, we need to define a special exception type to handle infeasible designs of heat exchangers. Infeasible designs arise in a number of cases when evaluating a network. These include attempting to exchange a negative amount of heat from a hot stream to a cold stream or if the temperatures of the hot and cold streams are incompatible, such as if the cold stream is actually hotter than the hot stream.
Exception types in Julia allow a function to indicate an error condition which can be caught by any function that led to the invocation of that function. This will be illustrated below in the definition of the heat exchanger type and its evaluation. The exception type defined is called Infeasibility:
1:struct Infeasibility <: Exception2:g # measure of infeasibility3:end
The <: construct defines Infeasibility as a sub-type of Exception. We could have re-used an existing Exception type, such as DomainError, but this would hide actual domain errors in the calculations, should these arise. A more focused exception type avoids hiding programming or modelling errors.
5.1.2.4. Heat exchanger
A heat exchanger is defined by the inlet and outlet temperatures of two streams, one hot and one cold, the driving force, the heat transfer coefficient, and duty resulting in an exchange area and corresponding cost:
1:struct Exchanger2:hot # hot stream temperatures3:cold # cold stream temperatures4:ΔT # log-mean temperature difference5:U # overall heat transfer coefficient6:A # area [m²]7:Q # duty [kW]8:cost # capital cost in currency units9:end
The actual design of an exchanger is undertaken when an instance of the structure representing an exchanger is created. The following function is a constructor for the Exchanger type. The design is based on the temperatures of the hot and cold streams and the amount of heat to exchange. The design will check for valid temperatures and for a positive amount to exchange. If any of those values is not reasonable, an exception is thrown (see lines 6, 15, and 26) and this exception will (hopefully) be caught by the code that attempted to create a specific exchanger.
Line 4 highlights that Julia can make use of a wide range of characters for naming variables such as an upper case Greek delta character. This can make the code more readable, matching the mathematical notation typically used more closely. The Julia REPL supports the use of \LaTeX{} syntax for entering such characters: \Delta in this case.
1:function Exchanger(hot, cold, Q, model)2:# define tuple of temperatures: (in, out)3:if hot isa Stream4:h = (hot.Tin, hot.Tin-Q/hot.mcp)5:if h[2] < hot.Tout6:throw(Infeasibility(hot.Tout-h[2]))7:end8:else9:h = (hot.Tin, hot.Tout)10:end11:# (in, out) for cold side as well12:if cold isa Stream13:c = (cold.Tin, cold.Tin+Q/cold.mcp)14:if c[2] > cold.Tout15:throw(Infeasibility(c[2]-cold.Tout))16:end17:else18:c = (cold.Tin, cold.Tout)19:end20:# temperature driving forces21:ΔT1 = h[1]-c[2]22:ΔT2 = h[2]-c[1]23:if ΔT1 ≤ 0.0 || ΔT2 ≤ 0.0 || Q ≤ 0.024:# indicate infeasibility using duty as25:# measure26:throw(Infeasibility(abs(Q)))27:end28:# Chen approximation to log mean temperature29:# difference30:ΔT = ( ΔT1 * ΔT2 * (ΔT1 + ΔT2)/2.0) ^ (1.0/3.0)31:# overall heat transfer coefficient32:U = 1.0 / (1.0/hot.h + 1.0/cold.h)33:# Area34:A = Q/U/ΔT35:# capital cost as a function of the area36:cost = model(A) # 6600.0 + 670.0 * A^0.8337:# create the object38:Exchanger(h, c, ΔT, U, A, Q, cost)39:end
Exchangers will be designed for both process integration where heat is transferred between two streams in the process itself as well as for meeting of heating or cooling demands through external utilities. In other words, either of the two streams may be an external utility but both could be process streams. With this in mind, some comments on the code, by line number, follow:
- The
hotstream may be an instance of a processStreamor anExternalUtility. For the former, the inlet is the actual inlet of the stream and the outlet of the hot stream after exchange is defined by the amount of heat transferred. - For an external utility, the temperature is fixed in the definition of the utility.
- The same calculations are performed for the cold stream which may be a process stream or an external utility.
- The differences in temperatures at both ends of the exchange are calculated, assuming counter-current operation of the exchange.
- The Chen approximation [Chen 1987] is used to determine the log-mean temperature difference, as estimate of the driving force for the exchange.
- The capital cost of the exchanger is a function of the area.
The following function overrides the default output for instances of the Exchanger type:
1:using Printf # make @printf available2:function Base.show(io :: IO, e :: Exchanger)3:@printf(io,4:"HEX(H:%.1f-%.1f C:%.1f-%.1f Q=%.2f: ΔT=%.2f U=%.3f A=%.2f %.2e cu)",5:e.hot[1], e.hot[2],6:e.cold[1], e.cold[2],7:e.Q,8:e.ΔT, e.U, e.A, e.cost)9:end
where the @printf macro from the Printf package is used to have more control over the formatting of the output.
We can test the Exchanger type by evaluating instances for different combinations of hot and cold streams and with external utilities:
1:using NatureInspiredOptimization.HEN: Stream2:streams = [Stream("h1", :hot, 1.0, 400, 120, 2.0)3:Stream("h2", :hot, 2.0, 340, 120, 2.0)4:Stream("c1", :cold, 1.5, 160, 400, 2.0)5:Stream("c2", :cold, 1.3, 100, 250, 2.0)]6:using NatureInspiredOptimization.HEN: ExternalUtility7:utilities = [8:ExternalUtility("steam", :hot,9:500.0, 500.0, 1.0,10:Q -> 120.0*Q)11:ExternalUtility("water", :cold,12:20.0, 30.0, 1.0,13:Q -> 20.0*Q) ]14:# try some designs15:using NatureInspiredOptimization.HEN: Exchanger16:Exchanger(streams[1], # hot stream17:streams[3], # cold stream18:100.0, # duty19:# cost model, function of area20:A -> 6600.0 + 670.0 * A^0.83)21:Exchanger(utilities[1],22:streams[4],23:150.0,24:A -> 6600.0 + 670.0 * A^0.83)25:Exchanger(streams[2],26:streams[3],27:360.0,28:A -> 6600.0 + 670.0 * A^0.83)
with output
HEX(H:400.0-300.0 C:160.0-226.7 Q=100.00:ΔT=156.07 U=1.000 A=0.64 7.06e+03 cu)HEX(H:500.0-500.0 C:100.0-215.4 Q=150.00:ΔT=339.04 U=0.667 A=0.66 7.08e+03 cu)ERROR: NatureInspiredOptimization.HEN.Infeasibility(360.0)
The code defines the streams, lines 1-5, the utilities, lines 6-13, and then designs three exchangers. The first exchanger, lines 16-20, exchanges 100 units of energy (W or kW, with actual units implied by the cost model) between the first hot stream and the first cold stream. The second exchanger, lines 21-24, exchanges 150 units of heat from the hot utility to the second cold stream. Finally, the third exchanger (lines 25-28) is intended to exchange the maximum amount of heat possible (360 units) between the second hot stream and the first cold stream. However, this design will not be feasible as the target temperature for the cold stream is hotter than the inlet temperature of the hot stream.
On lines 10, 13, 20, 24, and 28, anonymous functions are defined for estimating the capital cost of each exchanger and for the operating costs of the external utilities. These have the form of var -> function where var can be a single variable or an n-tuple. In the example, on line 10, a function which takes an argument Q is defined which returns the value of 120 times Q. The other lines define other anonymous functions. These cost models could have been defined as explicit functions with names but often such anonymous functions are clearer as they are defined where they are used.
The output (with lines reflowed to display properly here) shows the actual designs for the first and second exchanger and then an error message because an Infeasibility exception has been thrown. Following the exception, the REPL would in this case give information about where this exception took place. This information has not been shown. Later, we shall see that the value stored in the Infeasibility exception can be used as a measure of infeasibility for the search methods. The value, in the example above, is the amount of duty not exchanged due to the infeasible match.
5.2. Representation of a network superstructure
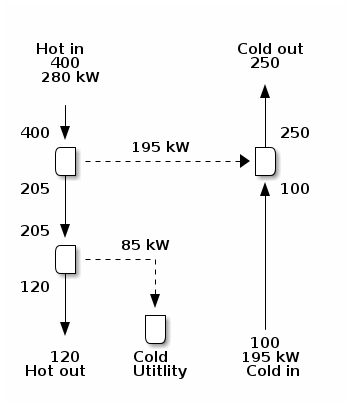
Figure 1: Example heat exchanger network graph showing one hot stream, one cold stream, one exchanger transferring 195 kW of heat from the hot stream to the cold streamd, and one utility exchanger used to remove the remaining desired heat, 85 kW, from the hot stream. Numbers without units are temperatures. There are two types of edges in this graph: solid lines for process streams, annotated with the temperature at each point, and dashed lines for heat transfer, both between process streams and with external utility. The nodes in the graph, indicated by boxes, represent half an exchanger and the dashed lines connect the two halves.
The solution to a heat exchanger network design problem is a directed graph that represents the flow of process streams and heat. An example network is shown in Figure 1. A graph which includes all possible exchanges between all the process streams and external utilities is known as a superstructure. The aim of the design method is to select, from this superstructure, the best actual network with exchangers designed to exchange heat as required. Defining a superstructure is challenging and so it is worth being able to represent such superstructures easily.
5.2.1. Grammar for superstructure representation
The aim is to define a simple representation of the graph, using text that can be typed in easily. This text representation will then be parsed and an appropriate data structure created which can subsequently be used for manipulation by the different optimization methods to generate network designs. A simple parser is presented below, similar to that used to interpret the genotype and phenotype representations used by a network design method inspired by techniques in the world of digital art [Fraga 2008].
The approach in defining the textual representation is best illustrated by an example. Consider the HEN problem defined in Table 1. An example string representation of the actions on one stream could be
c1 s < x h2 | x h1 > m u
which would be interpreted as split (s) the c1 stream with first branch having an exchange (x) with stream h2 and the second branch an exchange with stream h1; then mix (m) the results and meet any remaining heating requirements for this stream, c1, with an external utility (u).
For efficiency, both the explicit mix and utility directives can be removed. The split can be assumed to be followed by a mix operation when the definition of both branches is complete and every stream can be assumed to have a utility at the end to meet its un-met requirements. Therefore, this example would be:
c1 s < x h2 | x h1 >
This can be further simplified by assuming that any unrecognised token is an indication of an exchange, with the token being the descriptive name of the stream with which to exchange:
c1 s < h2 | h1 >
Now, if we number all the streams in the problem table in order, we can remove the labels on the exchange targets:
3 s < 2 | 1 >
where, in this case, c1 is the third entry in the table. The s is superfluous as it can be implied by the starting < of a split,
3 < 2 | 1 >
Finally, if we assume that all the streams will be given definitions, and these are in a list or vector structure, the stream identifier is not required:
< 2 | 1 >
It is this simplest representation that will be implemented.
This representation defines a superstructure because not all branches of a split need form part of a solution and each individual exchange noted in the representation will be optional. So, for instance, one network graph could consist of this third stream exchanging heat with the first stream alone.
The implementation will be based on a simple parser with the following BNF (Backus-Naur Form) representation of the language defined:
expr ::= <nil> | (action expr)action ::= ('<' expr '|' expr '>') | tokentoken ::= [0-9]+
where [0-9]+ means, in standard regular expression terminology, one or more digits.
5.2.2. Data structures for HEN representation
A heat exchanger network consists of a number of processing steps:
- heat exchangers, either integrated where heat is transferred from one process stream to another or for exchange of heat with external utilities;
- splitters which divert the flow of a stream into two flows, each of which may have different exchanges; and,
- mixers which bring together previously split streams.
These will be described by specific data structures and methods which work on these structures. They hold minimal data but will be used in the network representation to implement a state-task network [Kondili et al. 1993]. All the steps will be sub-types of the Step type defined here.
1:abstract type Step end2:3:# the start of a hot/cold stream4:struct Inlet <: Step5:inlet :: Stream6:end7:8:# the key step: exchange heat9:# between hot and col streams10:mutable struct Exchange <: Step11:hot :: Int12:cold :: Int13:match # should be a node14:Q :: Float6415:hex :: Union{Exchanger, Nothing}16:end17:18:# no-operation: an empty step19:struct Noop <: Step20:end21:22:# a set of steps, known as a segment,23:# is a step itself and will be used24:# for split & mix branches25:mutable struct Segment <: Step26:steps :: Vector{Step}27:end28:# some segments are a single step29:Segment(s :: Step) = Segment([s])30:31:# split the stream32:mutable struct Split <: Step33:η :: Union{Float64, Int}34:end35:36:# rejoin the split streams37:struct Mix <: Step38:end39:40:# meet demand with utility41:mutable struct Utility <: Step42:utility :: Union{ExternalUtility, Nothing}43:hex :: Union{Exchanger, Nothing}44:end
The data for each step include the design variable associated with the step, if any. For the Exchange type, \(Q \in [0,1]\) is heat to exchange between the hot and cold streams, as a fraction of how much is available in the hot stream, where match links up the hot and cold stream representations for evaluation, for instance the top dashed line in Figure 1. For Split, \(\eta \in [0,1]\) is the split fraction. How these design variables are used is described below when the optimization problem is defined.
5.2.3. Some utility functions
A Segment is a set of steps in the process with one inlet and one outlet. Some of the steps may be the individual branches that arise from a Split operation. Branches are represented by Segment steps, leading to the recursive use of segments: a segment may contain steps that are themselves segments.
The following two functions provide functionality for adding steps to a segment.
1:function append!(segment :: Segment, step :: Step)2:push!(segment.steps, step)3:end4:function append!(segment :: Segment, steps :: Vector{Step})5:for s ∈ steps6:if ! (s isa Noop)7:append!(segment, s)8:end9:end10:end
Some simple functions to override how the information in a network is presented:
1:function Base.show(io :: IO, segment :: Segment)2:print(io, " [")3:for s ∈ segment.steps4:print(io, s)5:end6:print(io, " ]")7:end8:Base.show(io :: IO, i :: Inlet) = print(io,"$(i.inlet)")9:function Base.show(io :: IO, x :: Exchange)10:print(io, " x:$(x.hot)→$(x.cold)")11:if nothing != x.hex12:print(io, " $(x.hex)")13:else14:print(io, " Q=$(x.Q)")15:end16:end17:Base.show(io :: IO, s :: Split) = print(io, " ⊣ η=$(s.η)")18:Base.show(io :: IO, m :: Mix) = print(io, " ⊢")19:function Base.show(io :: IO, u :: Utility)20:if nothing != u.hex21:print(io, " u:$(u.hex)")22:else23:print(io, " u")24:end25:end26:Base.show(io :: IO, n :: Noop) = print(io, "")
5.2.4. Implementation of parser
The parser takes textual representations, as presented in the previous section, and creates internal data structures which correspond to the network superstructure desired:
1:function parse(expression :: String, id :: Int)2:if nothing != (m = match(r"^ *(<|[0-9]+|\||>)",3:expression))4:s = m.captures[1]5:expression = replace(expression,6:r"^"*m.match => "")7:if s == "<"8:b1, expression = parse(expression, id)9:b2, expression = parse(expression, id)10:rest, expression = parse(expression, id)11:( [ Split(0.0) # split12:Segment(b1) # branch 113:Segment(b2) # branch 214:Mix() # come back together15:rest ], # remaining path16:expression )17:elseif s == "|"18:# end of first branch19:( Noop(), expression )20:elseif s == ">"21:# end of second branch22:( Noop(), expression )23:else24:# must be a stream id25:n = Meta.parse(s)26:# assume hot streams have lower index27:# than cold streams28:from, to = id < n ? (id, n) : (n, id)29:rest, expression = parse(expression, id)30:( vcat([Exchange(from, to, nothing,31:0.0, nothing)],32:rest),33:expression )34:end35:else36:( Utility(nothing, nothing), expression )37:end38:end
The key to the parser is using a regular expression to decode the representation into each of its components on line 2. A regular expressing in Julia is indicated by the letter r followed by a string. In this cases, the regular expression will match any amount of spaces at the start of the expression, ^ *, and then one of a number of alternatives: a split, <, a stream identifier consisting of one or more digits, [0-9]+, a branch separator, |, or the end of a split, i.e. a mix operation, >. The alternatives are enclosed in parentheses and separated by the vertical pipe character.
Following the regular expression, the match is now checked to see which of the alternatives was found. Each alternative will process the match and then return the set of steps generated along with what remains of the expression to parse.
For a split, the method recursively parses the remainder of the expression passed to this function, parsing the two branches and bracketing them with a Split and Mix pair of steps. If a stream identifier is found, an Exchange step is created which pairs up the current stream with the one identified in the representation.
I have also defined a parse method which can be applied to a set of stream representations, parsing each one in turn and adding the resulting sub-graphs to the overall network which consists of a vector of Segment instances:
1:function parse(expressions :: Vector{String})2:network = Segment[]3:for i ∈ 1:length(expressions)4:push!(network,5:Segment(parse(expressions[i], i)[1]))6:end7:network8:end
The following is a test of the parsing code. The assumption is that there are 4 streams with the first two being hot streams and the other two cold. The first stream can exchange with stream 3 and then stream 4. The second stream can exchange, in parallel, with streams 3 and 4. The third stream can exchange in parallel with streams 1 and 2 and, finally, the last stream can exchange with stream 1 first and then stream 2. Note that the parser does not ensure that the matches identified are either consistent (i.e if stream 1 wishes to match with stream 3, stream 3 should also indicate a match with stream 1) or feasible. This will be checked when the network is evaluated.
1:using NatureInspiredOptimization.HEN: parse2:begin3:expressions = ["3 4"4:"< 3 | 4 >"5:"< 1 | 2 >"6:"1 2"];7:network = parse(expressions)8:for s in 1:length(network)9:print(expressions[s])10:print(" -> ")11:println(network[s])12:end13:end
The output from this test is
3 4 -> [ x:1→3 Q=0.0 x:1→4 Q=0.0 u ] < 3 | 4 > -> [ ⊣ η=0.0 [ x:2→3 Q=0.0 ] [ x:2→4 Q=0.0 ] ⊢ u ] < 1 | 2 > -> [ ⊣ η=0.0 [ x:1→3 Q=0.0 ] [ x:2→3 Q=0.0 ] ⊢ u ] 1 2 -> [ x:1→4 Q=0.0 x:2→4 Q=0.0 u ]
5.3. Network model
Given the parsed information for each stream, we wish to represent the network in a data structure that allows us to traverse it easily and evaluate the network, given values for amounts to exchange and the split fractions (or binary choices).
The actual network is a directed graph, implementing the state-task network, with states represented by streams (as defined above) as the contents of edges and tasks represented by steps as the content of nodes [Emmerich et al. 2001].
- Edges
connect one node to another and carry process streams:
1:
mutable struct Edge2:from # node3:to # node4:stream # state5:id # unique id6:traversed # for evaluation7:end- Nodes
have any number of in and out edges:
1:
mutable struct Node2:in # edges3:out # edges4:step # task5:type # :hot or :cold6:id # unique id7:evaluated # for costing8:z # objective9:g # infeasibility10:end- Network
consists of sets of nodes and edges
1:
mutable struct Network2:inlets :: Vector{Node} # root nodes3:outlets :: Vector{Node} # leaf nodes4:edges :: Vector{Edge} # all edges in graph5:nodes :: Vector{Node} # all nodes in graph6:ne :: Int # next edge ID7:nn :: Int # next node ID8:# empty network constructor9:Network() = new(Node[], Node[],10:Edge[], Node[], 1, 1)11:endwhere some of the nodes have been identified as root or inlet nodes and leaves or outlet nodes.
Each of the above types has specific constructors and some ancillary functions:
1:function Edge(n :: Network)2:e = Edge(nothing, nothing, nothing, n.ne, false);3:add(n, e);4:e5:end6:function Edge(n :: Network, s :: Stream)7:e = Edge(nothing, nothing, s, n.ne, false);8:add(n, e);9:e10:end11:function Node(n :: Network, type)12:node = Node(nothing, nothing, nothing,13:type, n.nn,14:false,15:zeros(3),16:0.0);17:add(n, node);18:node19:end20:function Node(n :: Network, s :: Step, type)21:node = Node(nothing, nothing, s,22:type, n.nn,23:false,24:zeros(3),25:0.0);26:add(n, node);27:node28:end29:iscold(n :: Node) = n.type == :cold30:ishot(n :: Node) = n.type == :hot31:function add(network :: Network, edge :: Edge)32:push!(network.edges, edge)33:network.ne += 134:end35:function add(network :: Network, node :: Node)36:push!(network.nodes, node)37:network.nn += 138:end
Of special note is the initialization of nodes to have three values for the objective function (lines 15 and 24). For the HEN design problem, we will consider capital cost, operating cost, and exchange area potentially as separate criteria for optimization.
In Appendix 8, some functions for printing the structure of a HEN network are presented. I have moved these out of the way as they are long and messy and do not add much to the description of the design of such networks.
The next code block takes the parsed segment structures and creates the network graph:
1:function segment2graph(network :: Network,2:edge :: Edge,3:segment :: Segment,4:type)5:s = 1 # count through steps6:ns = length(segment.steps)7:first = true8:let root = nothing, leaf = nothing9:while s ≤ ns10:step = segment.steps[s]11:s += 112:# ignore Noop steps13:if ! (step isa Noop)14:node = Node(network, step, type)15:edge.to = node16:if first17:first = false18:root = node19:end20:node.in = [edge]21:if step isa Exchange22:edge = Edge(network)23:node.out = [edge]24:edge.from = node25:elseif step isa Split26:# first branch27:e1 = Edge(network)28:e1.from = node29:# next step should be a segment30:step = segment.steps[s]31:s += 132:# create a sub-graph from segment33:(root, leaf1) = segment2graph(network, e1, step, type)34:e1.to = root35:# second branch36:e2 = Edge(network)37:e2.from = node38:# connect branches to split node39:node.out = [e1, e2]40:step = segment.steps[s]41:s += 142:# create a sub-graph from segment43:(root, leaf2) = segment2graph(network, e2, step, type)44:e2.to = root45:# now join branches up: Mix46:step = segment.steps[s]47:s += 148:@assert step isa Mix "Expected a Mix after segments but got $step"49:node = Node(network, step, type)50:# out edges of each branch leaf51:# node are in-edges of the Mix52:# node53:node.in = vcat(leaf1.out,54:leaf2.out)55:leaf1.out[1].to = node56:leaf2.out[1].to = node57:# prepare to connect to what58:# follows59:oldedge = edge60:edge = Edge(network)61:node.out = [edge]62:edge.from = node63:elseif step isa Utility64:edge = Edge(network)65:node.out = [edge]66:edge.from = node67:else68:error("We should not get here")69:end70:# the last node will be a leaf of71:# the directed graph72:leaf = node73:else74:end75:end76:# return root and leaf of segment77:return (root, leaf)78:end79:end
The actual heat exchanger network superstructure, as a directed graph, can now be created using the network structures defined above along with the generation of segments from the representation of the network:
1:function createnetwork(streams, segments)2:@assert length(streams) == length(segments) "Need a segment for each stream and vice versa."3:network = Network()4:for i ∈ 1:length(streams)5:# create root (inlet) node for stream6:node = Node(network,7:Inlet(streams[i]),8:streams[i].type)9:push!(network.inlets, node)10:# first edge from root node is the stream11:edge = Edge(network, streams[i])12:edge.from = node13:node.out = [edge]14:# and this edge is connected to the graph15:# corresponding to the segment for this16:# stream17:(root, leaf) = segment2graph(network, edge, segments[i], streams[i].type)18:# the leaf is also remembered to allow for19:# backward traversal20:push!(network.outlets, leaf)21:end22:# link up all process stream exchanges23:matchexchanges(network)24:end
The network structure created by the function above is not fully connected. Missing are the actual exchange links between the hot and cold streams. Each end of the links is present in the hot and cold streams but they are not matched up yet. This is done on line 23, invoking the function defined below.
In this function, the sub-graph associated with each hot stream is traversed from root to leaf. If an exchange node is encountered, the cold streams are traversed in reverse order to find the appropriate matching exchange node. The cold streams are traversed in reverse order because we assume counter-current operation. The links we wish to create correspond to the exchanges illustrated by the top dashed line between the hot and cold streams in Figure 1.
1:function matchexchanges(network)2:for node ∈ network.nodes3:if ishot(node) && node.step isa Exchange4:# for each hot exchange node, look for5:# corresponding cold node, in reverse6:# traversal of cold stream7:for i ∈ length(network.nodes):-1:18:n = network.nodes[i]9:if iscold(n) && n.step isa Exchange10:# for cold side, link up the two11:# nodes if this cold node is not12:# already linked13:if n.step.hot == node.step.hot && n.step.cold == node.step.cold && nothing == n.step.match14:# link up15:n.step.match = node16:node.step.match = n17:break18:end19:end20:end21:@assert node.step.match != nothing "Did not find a match"22:end23:end24:network25:end
5.4. Problem definition
A heat exchanger network design problem is defined by the hot and cold streams, as illustrated in Table 1, the utilities available for meeting any unmet demands through external heating and cooling, the superstructure to consider for possible designs (section 5.2), and the cost model described in section 5.1 and implemented by the code in section 5.1.2.4.
To encapsulate the problem, we define an appropriate structure:
1:mutable struct HENS2:streams :: Vector{Stream}3:representation :: Vector{String}4:network :: Network5:hexmodel # f(A)6:tolerance :: Real7:utilities :: Vector{ExternalUtility}8:function HENS(s, r, h, t, u)9:network = createnetwork(s,parse(r))10:new(s, r, network, h, t, u)11:end12:end
5.4.1. Testing problem representation
Creating an instance of the HENS type creates the internal representation of the network by parsing the string representation. The following example consists of 2 hot streams and 2 cold streams. The representation specifies that the first hot stream will exchange first with the first cold stream and then with the second; the second hot stream will split and one branch will exchange with the first cold stream and the other with the second cold stream. The first cold stream splits and exchanges with each hot stream and the second cold stream receives heat from the first hot stream and then the second.
1:using NatureInspiredOptimization.HEN: HENS, Stream, ExternalUtility, evaluate, getVariables, printNetwork2:let problem = HENS(3:# streams: type Q Tin Tout h4:[Stream("h1", :hot, 1.0, 400, 120, 2.0)5:Stream("h2", :hot, 2.0, 340, 120, 2.0)6:Stream("c1", :cold, 1.5, 160, 400, 2.0)7:Stream("c2", :cold, 1.3, 100, 250, 2.0)],8:# structure representation9:["3 4", "< 3 | 4 >", "< 1 | 2 >", "1 2"],10:A -> 6600.0 + 670.0 * A^0.83, # hex cost11:# tolerance for negligible duty amounts12:1.0,13:[ExternalUtility("steam", :hot, 500.0, 500.0,14:1.0, Q -> 120.0*Q)15:ExternalUtility("water", :cold, 20.0, 30.0,16:1.0, Q -> 20.0*Q)]17:)18:printNetwork(problem.network)19:end

Figure 1: Adjacency network representation of the heat exchanger network superstructure. A greater than sign (>) in the diagonal indicates the start of a process stream to cool or heat. The numbers indicate edges connecting nodes (from the node for the row to the node for the column). The # symbol indicates the end of a stream and represents the final potential utility exchanger. A plus sign (+) indicates a continuation of the stream: another edge connecting two nodes. Each node has a cost and a measure of constraint violation and these are all zero as the network has not yet been evaluated.
The results of the above example is the network, printed out as an adjacency matrix (using code in Appendix 8). Instead of showing the actual output directly here, given the amount of text displayed by the printNetwork function, a screenshot is presented in Figure 1.
The evaluation of the network is implemented next.
5.5. Network evaluation
The evaluation of a network is a function of the design variables. These include the actual amounts to exchange between process streams, and implicitly with external utilities for any unmet demands, and the split fractions for branches in the network.
The actual amount to exchange between two streams will be defined by a fraction, \(q\), of the heat available in a hot stream for exchange to the cold stream, subject to the cold stream having sufficient need for this amount of heat. Therefore, for some values of \(q\), an instance of the network defined by the values of the design variables may be infeasible. Note that the cold streams will not have \(q\) design variables associated with them; only the hot streams will have these.
The split fraction, \(\eta\), will is the other design variable and every split operation will have one associated with it.
The following helper functions retrieve design variables, for those nodes that have such, and enable setting the values of those design variables.
1:getVariable(step :: Exchange) = step.Q2:getVariable(step :: Split) = step.η3:getVariables(problem :: HENS) = getVariables(problem.network)4:function getVariables(network :: Network)5:[getVariable(n.step)6:for n ∈ network.nodes7:if ((ishot(n) && n.step isa Exchange)8:|| n.step isa Split)]9:end10:11:setVariable(step :: Exchange, Q) = step.Q = Q12:setVariable(step :: Split, η) = step.η = η13:setVariables(problem :: HENS, vars) = setVariables(problem.network, vars)14:function setVariables(network :: Network, vars)15:map((n,v) -> setVariable(n.step,v),16:[n for n ∈ network.nodes17:if ((ishot(n) && n.step isa Exchange)18:|| n.step isa Split)],19:vars)20:end
Note the use of filtering for the getVariables function and both filtering and mapping for setVariables. Both are functional programming features of the Julia language. Functional programming makes it easy to traverse and work with iterable collections of data, such as the vector of nodes in the network. Filtering is used to extract specific elements from a collection. In lines 5 through 8, the values of the design variables from those nodes in the network that have design variables are extracted. Mapping applies a function to elements from one or more collections. On lines 15 through 19, the map function is used to assign each variable in vars to nodes in the network which are of the right type. These nodes are identified using filtering.
The filtering relies on introspection where the code can interrogate the runtime system as to the types of entities, such as nodes in the network. Also note that use of multiple dispatch for the setting and getting design variable values for the different steps, making the network setting and getting functions more straightforward, not requiring any check of the type of the step in each node.
Once design variables can be set, the evaluation is a matter of traversing the network and evaluating the individual nodes. The hot streams are traversed first as these will define the specified amount of head to exchange between hot and cold streams. Then the cold streams are traversed and the actual exchangers designed. If the amount of heat to exchange is more than the cold streams require, the design will be considered to be infeasible with the excess amount a measure of the infeasibility.
Three different measures of the performance of the network are defined: the total annualised cost, the total area for exchangers, both integrated and utility, and the total amount of heat removed or added using external utilities. This provides the capability to design to minimise any of these quantities or to consider the problem in a multi-objective sense.
Note that the evaluation code updates data in place for the network (the edges in particular) which means that this evaluation cannot be used with multi-processing. This can be addressed by making a deep copy of the network for the evaluation. I have not done so for simplicity.
1:function evaluate(vars, problem)2:network = problem.network3:setVariables(network, vars)4:# reset network: flags, costs, designs5:map(e -> (e.traversed = false), network.edges)6:for n in network.nodes7:n.evaluated = false8:n.z = [0.0, 0.0, 0.0]9:n.g = 0.010:if n.step isa Exchange || n.step isa Utility11:n.step.hex = nothing12:end13:end14:# evaluate whole network with breadth first15:# traversal: hot streams first16:while reduce(|,17:[(ishot(n) && !n.evaluated)18:for n ∈ network.nodes])19:for n ∈ network.inlets20:if ishot(n) && !n.evaluated21:evaluate(n, problem) # recursive22:end23:end24:end25:# now cold streams26:while reduce(|,27:[(!ishot(n) && !n.evaluated)28:for n ∈ network.nodes])29:for n ∈ network.inlets30:if !ishot(n) && !n.evaluated31:evaluate(n, problem) # recursive32:end33:end34:end35:# collect and add up objective function and36:# feasibility values37:(reduce(+, [n.z for n ∈ network.nodes]),38:reduce(+, [n.g for n ∈ network.nodes]))39:end
The network evaluation code also makes use of functional programming aspects of Julia. Specifically, in lines 5, 16-18, 26-28, and 37-38 the map and reduce operations are used. The map operation in line 5 shows the use of an anonymous function to initialise the traversal status of all the edges in the network. The other lines listed use reduction. Reduction applies the given operator, such as | for logical or and + for addition, to the elements of the collection given as second argument. In lines 16-18, the result of the reduce function is true if any element of the filtered network is true. Likewise in lines 26-28. Line 37 uses reduction to sum up the individual values of the objectives; line 38, similarly, adds up the constraint violations.
The evaluation of the network requires evaluation of all nodes (lines 21 and 31). Evaluation of nodes involved designing heat exchangers. A node can only be evaluated if all incoming edges have been traversed (breadth first traversal). This means that the stream associated with each incoming edge is up to date with the information required (temperatures, heat duty available or required). Once the node is evaluated, the procedure continues recursively to evaluate all nodes for the particular stream. The evaluation of a hot side of an exchange simply updates the temperatures and the actual heat duty to be exchanged with the cold stream. The evaluation of a cold stream exchange node designs the actual exchanger for the duty, as specified by the hot stream side.
1:function evaluate(node :: Node, problem :: HENS)2:# check if node is ready for evaluation3:if node.in == nothing ||4:reduce(&, [edge.traversed5:for edge ∈ node.in])6:# node can be evaluated which means designing7:# the processing step associated with it.8:design(node.step, node, problem)9:for i ∈ 1:length(node.out)10:node.out[i].traversed = true11:# recursively traverse graph12:if nothing != node.out[i].to13:evaluate(node.out[i].to, problem)14:end15:end16:node.evaluated = true17:end18:end
All nodes are traversed. Traversing a node determines the state of the outputs given the inputs by designing the process step associated with that node.
Using multiple dispatch, the appropriate design method is invoked by the type of processing step (line 8). The Inlet step copies the stream definition to the first Edge for the stream:
1:function design(step :: Inlet, node, problem)2:# copy stream to the first (& only) edge3:node.out[1].stream = Stream(step.inlet)4:end
Nodes associated with two specific steps, however, require an actual design: Exchange and Utility steps. For an integrated heat exchange, involving two process streams, the hot stream side of the match specifies the amount of heat to exchange. The cold stream side takes care of designing the actual exchanger, assuming that the match is feasible.
1:function design(step :: Exchange, node, problem)2:@assert length(node.in) == 1 "Exchange $type node expects one inlet"3:in = node.in[1].stream # inlet stream4:5:# actual exchange duty: if hot, it is defined by6:# the design variable (step.Q) as a fraction of7:# the available duty (in.Q); if a cold stream,8:# the value should have been set already when9:# the hot side was processed.10:if ishot(node)11:Q = step.Q * in.Q12:# tell cold side the amount to (potentially)13:# exchange14:step.match.step.Q = Q15:else16:Q = step.Q17:end18:# define the stream for the edge leaving this19:# node as being the same as the stream coming20:# in. This stream will be modified by the21:# exchange if an exchange actually takes place.22:# Very small values of a desired exchange are23:# ignored.24:node.out[1].stream = Stream(in)25:26:# only do any work if we have an actual amount27:# to exchange; note that a negative value28:# indicates that the hot stream wished to give29:# away more heat than the cold stream can30:# accept. This will be caught in the design of31:# the exchanger.32:if abs(Q) > problem.tolerance33:if Q ≤ in.Q34:T = in.Tin + (Q/in.Q)*(in.Tout-in.Tin)35:# duty for stream is adjusted36:node.out[1].stream.Q = in.Q-Q37:# as is the inlet temperature38:node.out[1].stream.Tin = T39:# if cold stream, design actual exchanger40:if ! ishot(node)41:try42:node.step.hex = Exchanger(43:step.match.in[1].stream,44:in,45:Q,46:problem.hexmodel)47:# three criteria48:node.z = [node.step.hex.cost,49:node.step.hex.A,50:0.0]51:catch e52:# the design may fail (Q<0, ΔT<0)53:if e isa Infeasibility54:node.g = e.g55:else56:# something else went wrong57:# so propagate error upwards58:throw(e)59:end60:end61:end62:else63:# infeasible exchange: violation is64:# difference between heat required and65:# heat available66:node.g = abs(Q-in.Q)67:end68:end69:end
Lines 41 through to 60 handle exceptions. The code to execute comes after the try statement up to but not including the catch statement. If during the execution of this code, an exception is thrown, control will be passed to the catch clause. In this clause, the type of exception is checked (line 53). If the exception is Infeasibility, it indicates that the exchanger could not be designed due to the temperatures not being suitable or that a negative amount of heat to exchange has been requested. If the exception thrown is of any other type, the exception is propagated back to the caller of this function (line 20).
The second processing step that requires a design is for heat exchange with an external Utility:
1:function design(step :: Utility, node, problem)2:@assert length(node.in) == 1 "Exchange $type node expects one inlet"3:# inlet stream only4:in = node.in[1].stream5:# design an actual exchange if the amount to6:# heat/cool is significant. This caters for7:# rounding errors in the processing of the heat8:# duties in getting to this node.9:if in.Q > problem.tolerance10:try11:# find appropriate utility; assume12:# utilities specified in order of13:# increasing cost so first suitable one14:# will do15:found = false16:for u ∈ problem.utilities17:if ishot(node) && !ishot(u) &&18:in.Tout > u.Tout19:found = true20:node.step.hex = Exchanger(21:in, u, in.Q,22:problem.hexmodel)23:utilitycost = u.model(in.Q)24:# three criteria25:node.z = [26:node.step.hex.cost + utilitycost,27:node.step.hex.A,28:in.Q ]29:# leave loop as utility found30:break31:elseif !ishot(node) && ishot(u) &&32:in.Tout < u.Tout33:found = true34:node.step.hex = Exchanger(35:u, in, in.Q,36:problem.hexmodel)37:utilitycost = u.model(in.Q)38:# three criteria39:node.z = [40:node.step.hex.cost + utilitycost,41:node.step.hex.A,42:in.Q ]43:# leave loop as utility found44:break45:end46:end47:if !found48:# no suitable external utility has49:# been found so we throw an50:# exception51:throw(Infeasibility(in.Q))52:end53:catch e54:if e isa Infeasibility55:node.g = e.g56:else57:# something else went wrong58:# so propagate error upwards59:throw(e)60:end61:end62:elseif in.Q < -problem.tolerance63:node.g = abs(in.Q)64:end65:end
Of note in this function is that it not only handles exceptions thrown by the Exchanger design, it may throw its own exception (line 51) if there is no suitable utility.
The Split and Mix steps do not involve any actual design but do require creating the streams that leave the step. Splitting simply creates two identical streams except that the amount heat to remove or add is split according to the η design variable.
1:function design(step :: Split, node, problem)2:in = node.in[1].stream3:mcp = [step.η, (1-step.η)] * in.mcp4:for i ∈ 1:25:s = Stream(in)6:s.mcp = mcp[i]7:s.Q = abs(s.mcp*(s.Tout-s.Tin))8:node.out[i].stream = s9:end10:end
The mixing step defines an outlet stream whose inlet temperature is a weighted average of the two inlet streams.
1:function design(step :: Mix, node, problem)2:in = [node.in[1].stream, node.in[2].stream]3:node.out[1].stream = Stream(in[1])4:mcp = in[1].mcp + in[2].mcp5:Q = in[1].Q + in[2].Q6:if Q > eps()7:if ishot(node)8:Tin = in[1].Tout + Q/mcp9:else10:Tin = in[1].Tout - Q/mcp11:end12:node.out[1].stream.mcp = mcp13:node.out[1].stream.Q = Q14:node.out[1].stream.Tin = Tin15:else16:node.out[1].stream.Tin = in[1].Tout17:end18:end
The inlet for a stream has no step associated with it.4 The outlet stream should have already been defined in the creation of the node so the design of the step for this node requires no work.
1:function design(s :: Nothing, node, problem)2:end
Finally, the Noop step simply copies the inlet stream to the outlet:
1:function design(step :: Noop, node, problem)2:node.out[1].stream = Stream(node.in[1].stream)3:end
5.5.1. Evaluation tests
To test out the HENS evaluation codes, we consider a number of small examples. All are based on two process streams with both steam and cooling water available as utilities and using the same area cost function for the exchangers:
1:using NatureInspiredOptimization.HEN: Stream, ExternalUtility2:streams = [3:# streams: type Q Tin Tout h4:Stream("h1", :hot, 1.0, 400, 120, 2.0)5:Stream("c1", :cold, 1.3, 100, 250, 2.0)6:]7:utilities = [8:# external utilities: type Tin Tout h9:ExternalUtility("steam", :hot, 500.0, 500.0, 1.0,10:Q -> 120.0*Q) # cost function11:ExternalUtility("water", :cold, 20.0, 30.0, 1.0,12:Q -> 20.0*Q)13:]14:# cost of exchanger, function of area A15:cost(A) = 6600.0 + 670.0 * A^0.83
The first case is a superstructure that has no exchanges between process streams, expecting to meet all demands from external utilities:
1: representation = ["", ""]
With these definitions, the actual heat exchanger network design problem can be created:
1:using NatureInspiredOptimization.HEN: HENS2:problem = HENS(streams, # streams3:representation, # superstructure4:cost, # cost function5:# ignore any duties less than this6:# amount7:1.0, # threshold8:utilities) # utilities
Once the problem has been defined, we can query the problem to determine the design variables and we can evaluate the problem with the variables as given:
1:using NatureInspiredOptimization.HEN: evaluate, getVariables2:using Printf3:v = getVariables(problem)4:z, g = evaluate(v, problem)5:@printf("Network criteria: (%.2e, %.2e, %.2e)\n",6:z[1], z[2], z[3])7:@printf("with constraint: %.1f\n", g)
which results in this output:
Network criteria: (4.40e+04, 2.96e+00, 4.75e+02) with constraint: 0.0
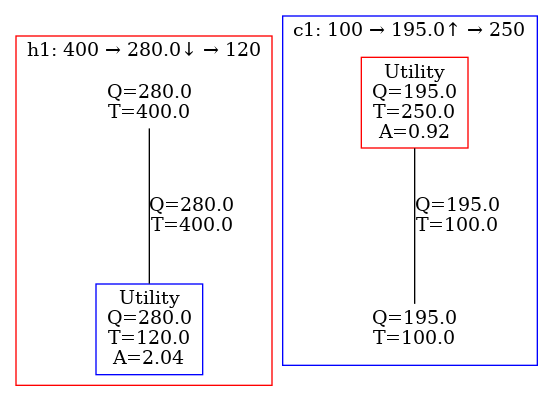
Figure 1: The network obtained evaluating the first heat exchanger network test problem.
This output presents the cost, the total exchanger area, and the amount of utility used, as well as indicating that this evaluation was feasible as the constraint violation is 0. The result of the draw function (see Appendix 8) is shown in Figure 1.
Using the same streams, we can specify a representation which includes an exchange between the hot and cold streams:
1: representation = ["2", "1"]
The hot stream has more heat available than the cold stream requires so an exchange specification on the hot stream will be infeasible if it results in more than the cold stream needs. Therefore, valid values for \(Q\), as the single design variable, will be \(Q \in [0.0, 195.0/280.0]\), the upper bound being the ratio of the amount of heat the cold stream can accept and the amount of heat the hot stream wishes to give away.
The test considers 4 different designs, one with no exchange (which should match the above test), one with half of the amount the hot stream has, one with the exact amount that the cold stream needs, and finally one with the full amount the hot stream has available:
1:using NatureInspiredOptimization.HEN: evaluate, getVariables2:using Printf3:v = getVariables(problem)4:@printf "| q | cost | area | utility | constraint |\n"5:@printf "| ∈ [0,1] | | m^2 | | |\n|-\n"6:for q ∈ [0.0, 0.5, 195.0/280.0, 1.0]7:v = [q] # one design variable8:(z, g) = evaluate(v, problem)9:@printf("| %.3f | %.0f | %.2f | %.0f | %.0f |\n",10:q, z[1], z[2], z[3], g)11:end
| q | cost | area | utility | constraint |
|---|---|---|---|---|
| ∈ [0,1] | m2 | |||
| 0.000 | 44035 | 2.96 | 475 | 0 |
| 0.500 | 30863 | 2.45 | 195 | 0 |
| 0.696 | 16505 | 2.50 | 85 | 0 |
| 1.000 | 30623 | 0.92 | 195 | 85 |
Table 1 shows the output from the code. As expected, the cost reduces as the amount of heat exchanged increases. However, if the amount of heat to be exchanged exceeds that required by the cold stream, the constraint is violated. In that case, g indicates a measure of the violation, 85 kW in this case (the difference between 280 and 195). When an infeasible design is identified, the values of the other criteria should be ignored as a complete design has not been achieved.
5.6. Optimization
With the evaluate method defined, we can now use the solvers to find solutions to more complex network structures. The evaluation provides up to three criteria that may be used for the optimization procedures. The following define three different objective functions based:
- annualised cost
including the capital cost of all exchangers and the cost of the external utilities:
1:
function cost(v, problem)2:z, g = evaluate(v, problem)3:(z[1], g)4:end- total heat exchanger area
of both integrated exchangers and those with external utilities:
1:
function area(v, problem)2:z, g = evaluate(v, problem)3:(z[2], g)4:end- total amount of heat
provided or taken away by external utilities:
1:
function utility(v, problem)2:z, g = evaluate(v, problem)3:(z[3], g)4:end
These criteria can be used singly or in combination. The latter case defines multi-objective optimization design problems.
5.6.1. Case study: One hot stream, two cold streams
The first design problem considered is based on the problem posed by Biegler et al. [Table 16.6 Biegler et al. 1997:552]. The streams and external utilities are defined here:
1:using NatureInspiredOptimization.HEN: Stream, ExternalUtility2:# streams: type Q Tin Tout h3:streams = [4:Stream("h1", :hot, 22.0, 440, 350, 2.00)5:Stream("c1", :cold, 20.0, 349, 430, 2.00)6:Stream("c2", :cold, 7.5, 320, 368, 0.67) ]7:utilities = [8:ExternalUtility("steam", :hot, 500.0, 500.0,9:1.0, Q -> 120.0*Q)10:ExternalUtility("water", :cold, 300.0, 320.0,11:1.0, Q -> 20.0*Q) ]12:areacost(A) = 6600.0 + 670.0 * A^0.83
The superstructure for possible network designs allows for the hot stream to match with both cold streams in any order and also allows for splitting of the hot stream to consider parallel exchanges. Detail can be found in the citation above. The closest representation in the system I have implemented consists of two splits and two heat exchangers:
1:representation = ["< 2 | 3 > < 2 | 3 >", # h12:"1 1", # c13:"1 1"] # c2
The solution obtain by [Biegler et al. 1997] has an objective function value of 77,972 USD y-1. Interestingly, one of the heat exchangers makes the hot stream colder than desired but the resulting mix reaches the target temperature exactly.5 The evaluation implemented above will not allow for this as exchanges can not lead to outlet temperatures outside the temperature intervals defined by the streams. The evaluation process could be modified to cater for this should it be desirable.
As the superstructure defined for the problem in [Biegler et al. 1997] cannot be exactly represented in our implementation, we do not necessary expect to obtain the same results. On the other hand, the problem, as formulated in this book, is tackled as a single optimization problem instead of a sequence of embedded optimization problems. In the problem formulation provided by Biegler et al., the outer optimization minimises area cost subject to the minimization of the number of units, itself subject to a minimum utility cost. Our problem formulation is to minimise the total annualised cost, including both heat exchangers (cost as a function of area) and utility costs. A problem formulation taking all aspects into account simultaneously has the potential to find better solutions, should they exist.
The heat exchanger network design problem can now be specified, bringing together the above details:
1:using NatureInspiredOptimization.HEN: HENS, evaluate, getVariables2:problem = HENS(streams,3:representation,4:areacost,5:1.0,6:utilities)7:v = getVariables(problem)8:# base case: no exchanges9:evaluate(v, problem)
For consistency, the initial population will be created in the same way and with the same number of points for all the methods. However, each time the problem is attempted, a different initial population will be used.6
1:using NatureInspiredOptimization: Point, randompoint2:using NatureInspiredOptimization.HEN: cost3:n = length(v) # number of design variables4:np = 10*n # population size5:# lower and upper bounds: all variables ∈ [0,1]6:lower = zeros(n)7:upper = ones(n)8:# create initial population including bounds9:# and random points10:p0 = [ Point(lower, cost, problem)11:Point(upper, cost, problem)]12:while length(p0) < np13:push!(p0, Point(randompoint(lower, upper),14:cost, problem))15:end
The application of each method is now presented:
- Genetic Algorithm
use the
costobjective function and the full population size specified above:1:
using NatureInspiredOptimization.GA: ga2:best, p, ϕ = ga(3:p0, # population4:cost, # objective function5:parameters = problem, # HEN superstructure6:lower = lower, # lower bounds7:nfmax = 5e6, # function evaluations8:np = np, # population size9:upper = upper # upper bounds10:)- Particle swarm optimization
as with the genetic algorithm, full population size and the same objective function:
1:
using NatureInspiredOptimization.PSO: pso2:best, p = pso(3:p0, # population4:cost, # objective function5:parameters = problem, # HEN definition6:lower = lower, # lower bounds7:nfmax = 5e6, # function evaluations8:np = np, # population size9:upper = upper # upper bounds10:)- Plant Propagation Algorithm
this method has a smaller population, so only two times the number of design variables instead of ten, and the same objective function:
1:
using NatureInspiredOptimization.PPA: ppa2:best, p, ϕ = ppa(3:p0, # population4:cost, # objective function5:parameters = problem, # HEN definition6:lower = lower, # lower bounds7:nfmax = 5e6, # function evaluations8:np = 2*n, # population size9:upper = upper # upper bounds10:)
The output after each nature inspired optimization method has been considered includes the best solution in the final population:
1:using NatureInspiredOptimization: printvector2:using NatureInspiredOptimization.HEN: evaluate, setVariables3:printvector("| best: |", best.x, "| ")4:println("with objective function value $(best.z).")5:setVariables(problem, best.x)6:z, g = evaluate(best.x, problem)7:println("\nfinal: $z $g")
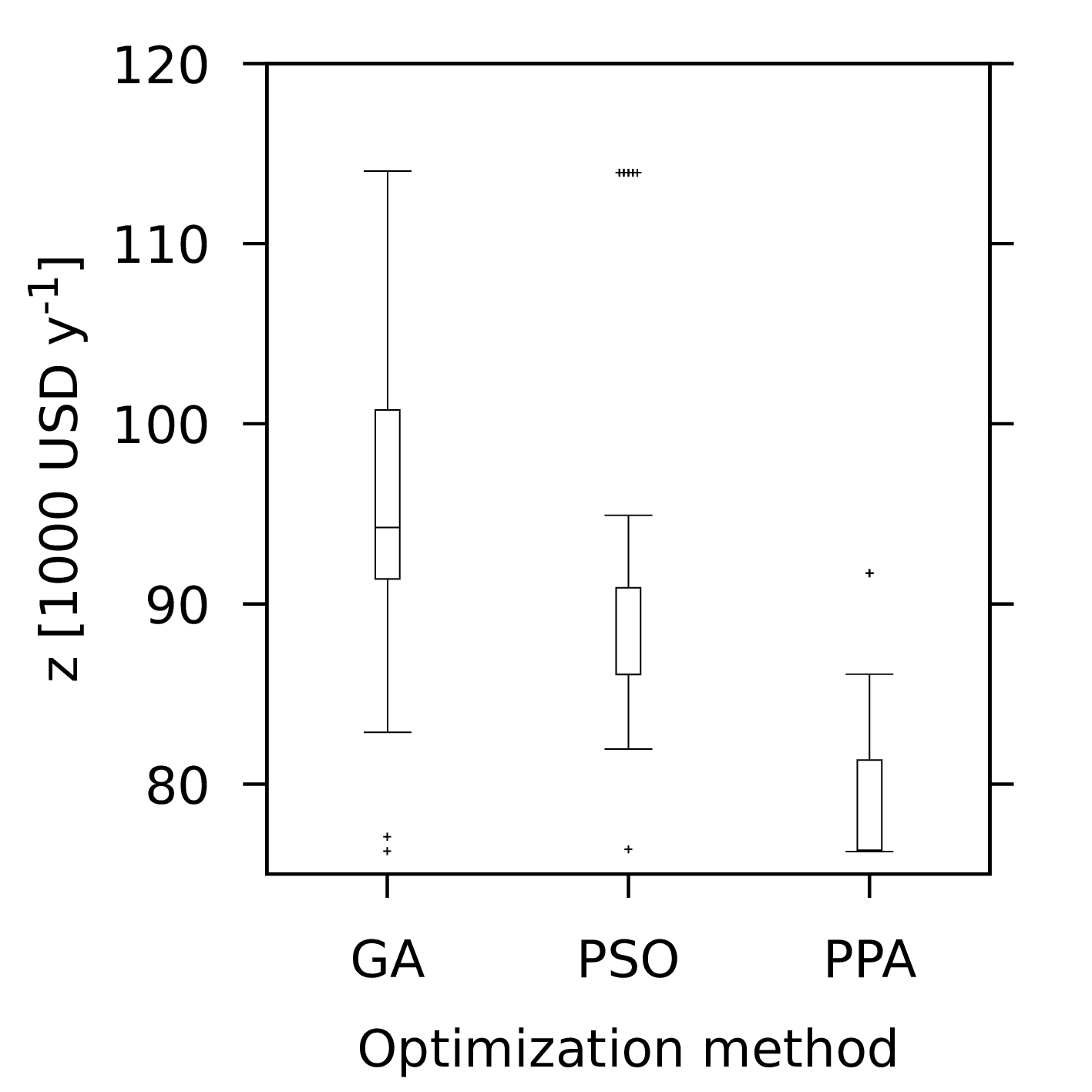
Figure 1: Box plot of results obtained from 10 runs for each of the three nature inpired optimization methods: the genetic algorithm, the particle swarm optimization method, and the plant propagation algorithm. The tolerance was set to 1.0.
Figure 1 shows the results obtained with the three methods, using the parameter values for each method that has been seen to be appropriate in the previous case studies. The results show that the PPA method most consistently returns good designs, with some cases having values of the objective function close to that presented in [Biegler et al. 1997]. The GA and PSO methods, however, show less favourable behaviour. Figure 1 shows the best result obtained with the PPA.
It should be noted that the cost of the design based on no integration at all, i.e. meeting all heating and cooling requirements from utility alone, is 322.4 kUSD y-1. All methods, therefore, improve significantly on this cost.
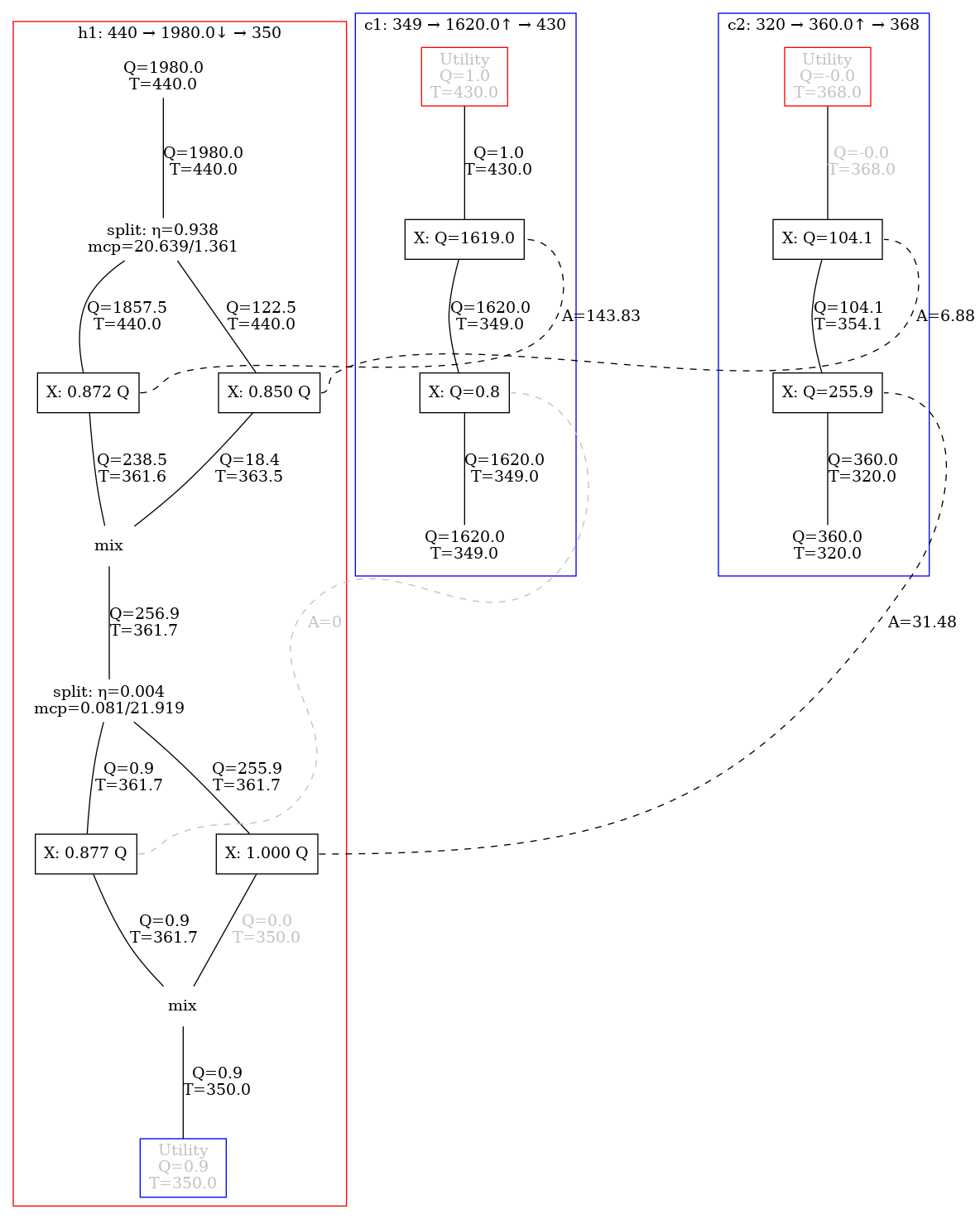
Figure 1: The network diagram for the best solution obtained using the PPA. This involves three exchangers and all demands are met by integrated exchanges, not requiring any external utility.
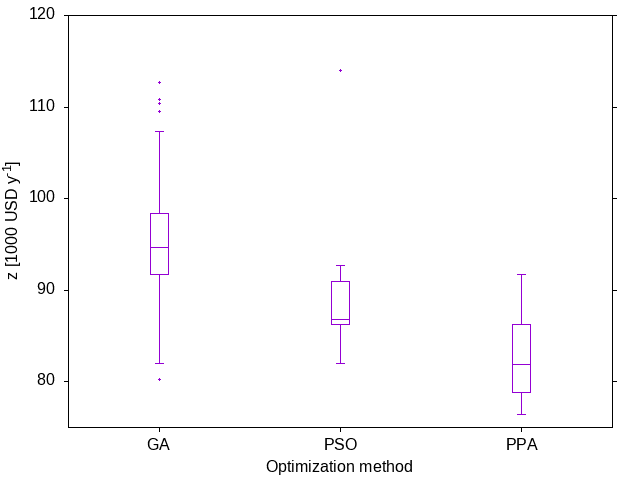
Figure 1: Box plot of the results obtained from 100 runs for each of the three nature inspired optimization methods, with a tolerance value of 0.1.
Figure 1 shows the results obtained with a much more stringent tolerance value. Recall, the tolerance value indicates values of duty that can be ignored, both for integrated exchanges and for external utility. The results are similar, when compared with Figure 1, which used a tolerance of 1.0. The main differences are the broadening of the range of results obtained with the PPA and the loss of the best solutions for the GA and PSO methods. Otherwise, the relative performance remains the same.
The main reason for the variation in outcomes for not only the PPA but for all three methods is that the boundaries of the domain on the design variables, values of 0 or 1, have significant qualitative meaning. The majority of the solutions obtained have values close to either 0 or 1 for the two split fractions. The methods would probably benefit from boundary mutation operators, operators that would have a tendency to push variables to their boundaries. This has previously been seen in the use of hybrid methods, and methods which involved the human designer as well [Fraga 2006].
5.6.2. Case study: two hot & two cold streams
The second case study, presented at the start of the heat exchanger network design problem, Table 1, is the design of a heat exchanger network for a process with two hot streams and two cold streams, with two external utilities available to meet excess requirements, and where the operating and capital costs are the same as for the first case:
1:using NatureInspiredOptimization.HEN: Stream2:streams = [ Stream("h1", :hot, 1.0, 400, 120, 2.0)3:Stream("h2", :hot, 2.0, 340, 120, 2.0)4:Stream("c1", :cold, 1.5, 160, 400, 2.0)5:Stream("c2", :cold, 1.3, 100, 250, 2.0) ]6:using NatureInspiredOptimization.HEN: ExternalUtility7:utilities = [8:ExternalUtility("steam", :hot, 500.0, 500.0,9:1.0, Q -> 120.0*Q)10:ExternalUtility("water", :cold, 20.0, 30.0,11:1.0, Q -> 20.0*Q)12:]13:areacost(A) = 6600.0 + 670.0 * A^0.83
The superstructure in this case allows each hot stream to match with each cold stream twice and vice versa:
1:representation = [2:"< 3 | 4 > < 3 | 4 >", # h13:"< 3 | 4 > < 3 | 4 >", # h24:"< 1 | 2 > <1 | 2>", # c15:"< 1 | 2 > <1 | 2>" # c26:]
This superstructure defines sixteen design variables: eight for the split fractions and eight for the possible exchangers.
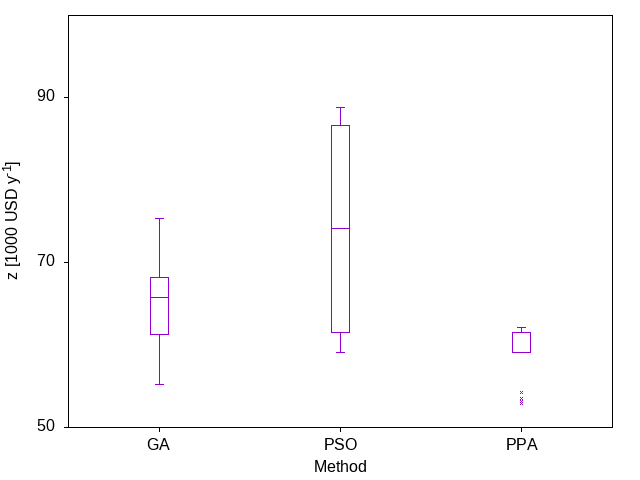
Figure 1: Box plots of the outcome from solving the second heat exchanger network design case study 100 times with each method.
The problem is defined the same was as as for case 1, using the variables defined in these code blocks above, as is the initialization of the population. The nature inspired optimization methods are also invoked in the same way (using exactly the same code). Figure 1 shows the outcome from 100 runs for each method. For this case study, the genetic algorithm performs better than the particle swarm method. The plant propagation algorithm continues to perform best of all, showing more consistency in outcome and, in this case, having a few outliers that are significantly better.
The plant propagation algorithm finds the network shown in Figure 1, as an example. The average result obtained by the plant propagation algorithm is the same structure but with a utility requirement for the first hot stream. When this result is obtained, the person involved would typically be able to see that small tweaks to the design variables would remove the need for the extra exchanger and the small amounts of external utility. The optimization methods fail to find this solution in most cases because it requires very precise tuning of the design variables. This highlights the deficiency in this modelling approach although good the methods do identify good starting points for further refinement [Fraga 2006].
Figure 1: The best network found, using the Plant Propagation Algorithm, with an objective function value of 53 kUSD. Heat exchanges are indicated by dashed lines and boxes indicate one half of an exchanger with the dashed lines connecting corresponding halves. The first hot stream exchanges 85 kW with the first cold stream and then 195 kW with the second cold stream. The second hot stream exchanges 222.4 kW with the first cold stream. Both the first hot stream and the second cold stream have all their demands met by integrated exchanges, requiring no external utilities.
5.7. Summary
The heat exchanger network design problem is significantly more complex than the other problems I have presented in this book. The model, for mathematical programming approaches, is challenging to develop. To quote from [Burre et al. 2022]:
To overcome the considerable manual effort and benefit from a flexible application of different reformulation approaches given specific problem characteristics, the automated generation of problem formulations […] would be beneficial.
For this reason, the approach I have taken is to enable the superstructure required for finding heat exchanger network designs to be represented using a simple grammar. The representation is converted into a directed graph which can subsequently be traversed to evaluate alternative designs.
The results in this chapter show that this approach works in at least identifying promising structures. The challenges that remain are firstly to be able refine the solutions obtained to remove unnecessary exchanges and, from a user perspective, to define more complex superstructure representations when the number of streams increases. Optimization can play a part in addressing both of these challenges. The latter could be addressed by converting the problem of specifying a representation for the superstructure into an optimization task iteself well [Fraga 2008]. Implementing this task is left as an exercise to the reader. The former issue, of fine-tuning solutions obtained, could be addressed by considering hybrid procedures [Fraga 2006], combining meta-heuristic methods with, for instance, gradient based methods, and often by involving the designer directly to suggest directions for improvements.
6. Conclusions
This book has presented three nature inspired optimization methods. These methods have been used to solve three problems illustrating different challenges in process systems engineering and the suitability of the methods. Although the codes presented have been written for the intent of demonstrating how to use Julia, the case studies have shown that the codes are fully functional and robust. As such, they are usable in general.
Nevertheless, there are many aspects that could be extended or improved in all three methods. The following is a list of some aspects that could be considered in further developing these codes:
- diversity control
- All three methods are population based. There is no control over the diversity in the populations so it is possible, and often likely, that the population may end up representing a small part of the search domain without having found globally good solutions [Raquel and Naval 2005].
- parallel implementations
- Although I have illustrated the use of the multi-processing in the implementation of the plant propagation algorithm, all three methods can benefit from using this capability.
- convergence properties
- Along with diversity, there may be a need to adapt the evolutionary aspects of each method to avoid premature convergence to local optima.
- hybrid methods
- The last case study shows that these nature inspired optimization methods, as I have implemented in this book, may not be able to fine-tune the design variables to the degree required to find the best solutions. One possible approach that could improve these methods is the use of deterministic local solvers in combination with the meta-heuristic methods.
- selection methods
- The genetic algorithm and the plant propagation algorithm both use the size 2 tournament selection method. Many other methods are possible for selecting solutions.
- population updates
- The genetic algorithm and the plant propagation algorithm create a new population at each iteration. Different methods for evolving the population could be implemented, including for instance a continuously evolving approach where new solutions are inserted in a single population and made available immediately for selection.
- fitness methods
- The rank based fitness method appears to work well, especially in the context of multiple objectives. However, other fitness measures could be implemented. For multi-objective optimization, the non-dominated sorting approach is popular.
One of the key aims of this book is to illustrate how Julia can be used to implement not just the optimization methods but also the models for process systems engineering. Many aspects of Julia have been mentioned or highlighted but it is the case that many other aspects have not been mentioned. These include the following:
- macros
- Some macros have been used, most notably the
Threads.@threadsmacro. Writing your own macros can be useful for modelling and the creation of domain specific languages. - debugging
When working with complex models, it may be necessary to debug the code created. There is support for debugging in Julia through, for instance, the Debugger.jl package.
- profiling
- Complex problems in process systems engineering are often computationally demanding. Profiling code to identify the particular parts that require the most computation can be useful for improving the performance. Julia has the Profile module.
- functional programming
- There are many constructs in the Julia language the support a functional programming approach. I have illustrated a few of these in the book but there many others, including, for instance, data flow with pipes and function composition.
In summary, this book has presented three nature inspired optimization methods. Their performance has been considered, mostly in terms of outcome obtained. All three methods are similar in terms of computational impact. The particle swarm method seems to be quicker at finding good solutions but converges prematurely without a full search of the domain. The genetic algorithm performs better in terms of overall outcome but it is the plant propagation algorithm that most consistently finds the best solutions.
7. Appendix. The Nature Inspired Optimization module
The code in this book can be found in my github repository. The code is implemented as a Julia package which consists of a main module, defined in this appendix below. This module includes the code presented in the book, both the individual nature inspired optimization methods and the case studies.
1:module NatureInspiredOptimization2:3:# external packages required4:using Printf # for the @printf macro5:6:# utility functions and common structures for the7:# nature inspired optimization methods8:include("definitions.jl")9:10:# chlorobenzene process optimization11:module Chlorobenzene12:include("chlorobenzene.jl")13:end14:15:# penicillin fermentation process operation16:module PFR17:include("PFR.jl")18:end19:20:# heat exchanger network design21:module HEN22:include("HEN.jl")23:end24:25:# the genetic algorithm26:module GA27:include("GA.jl")28:end29:30:# the particle swarm optimization method31:module PSO32:include("PSO.jl")33:end34:35:# the plant propagation algorithm36:module PPA37:include("PPA.jl")38:end39:40:end # module
8. Appendix. Supplementary HEN functions
This appendix includes code for displaying heat exchanger networks, both textually and using a graph visualization tool.
8.1. Textual output
The follow code is mostly for debugging and prints out the full contents of the graph structure representing the network superstructure:
1:Base.show(io :: IO, e :: Edge) = e.stream == nothing ? print(io, "e$(e.id)<ϕ>") : print(io, "e$(e.id)<$(e.stream)>")2:Base.show(io :: IO, n :: Node) = n.step == nothing ?3:print(io, "n$(n.id)<ϕ>") :4:(@printf(io, "n%d[(%.2e,%.2e,%.2e),%.1f]",5:n.id,6:n.z[1], n.z[2], n.z[3],7:n.g),8:print(io, " <$(n.step)>"))9:function dump(desc :: String, edge :: Edge)10:println("$edge: $desc")11:println(": from = $(edge.from)")12:println(": to = $(edge.to)")13:end14:function dump(desc :: String, node :: Node)15:println("$node: $desc")16:println(": in = $(node.in)")17:println(": out = $(node.out)")18:println(": step = $(node.step)")19:end20:function traverse(io :: IO, node :: Node)21:if node isa Node22:print(io, node)23:if node.out == nothing24:print(io, "□")25:else26:for edge ∈ node.out27:print(io, edge)28:if edge.to == nothing29:print(io, "?")30:else31:traverse(io, edge.to)32:end33:end34:end35:else36:print(io, "□")37:end38:end39:function Base.show(io :: IO, network :: Network)40:for node ∈ network.inlets41:traverse(io, node)42:println(io)43:end44:end
8.2. Adjacency matrix presentation of network
The network superstructure, a directed graph, can be represented using an adjacency matrix. This code prints out the network using such a matrix:
1:using Printf2:function printNetwork(network :: Network)3:n = length(network.nodes)4:c = Matrix{String}(undef, n, n)5:for i ∈ 1:n # for each node6:for j ∈ 1:n7:c[i,j] = " "8:end9:node = network.nodes[i]10:if nothing != node.in && length(node.in) > 011:if nothing != node.out && length(node.out) > 0 && any(e.to != nothing for e in node.out)12:c[i,i] = " +-"13:else14:c[i,i] = " # "15:end16:else17:c[i,i] = " >-"18:end19:for e ∈ node.out20:if nothing != e.to21:out = e.to22:c[i,out.id] = @sprintf "%2d" e.id23:for j ∈ i+1:out.id-124:c[i,j] = "---"25:c[j,out.id] = "|"26:end27:end28:end29:end30:# top line of matrix31:@printf " +-"32:for i ∈ 1:n33:@printf "%3d" i34:end35:@printf "-+\n"36:for i ∈ 1:n37:@printf "%3d. | " i38:for j ∈ 1:n39:@printf "%-3s" c[i,j]40:end41:@printf " | %s\n" network.nodes[i]42:end43:# bottom line of matrix44:@printf " +-"45:for i ∈ 1:n46:@printf "%3d" i47:end48:@printf "-+\n"49:# now detail on the nodes and edges50:println("Nodes:")51:for node ∈ network.nodes52:@printf "%3d. %s\n" node.id node53:end54:println("Edges:")55:for edge ∈ network.edges56:@printf "%3d. %s\n" edge.id edge57:end58:end
8.3. Graphical network representation
A graphical representation is useful to help understand the results of evaluating a network. Generating pleasing diagrams automatically is a challenging task and is out of the scope of this book. I have previously implemented automated tools for HEN layout and graphical presentation [Fraga et al. 2001a; Fraga 2009]. Here, I present code which delegates the responsibility for the generation of the graphical representation to an existing generic graph drawing and layout software, specifically the Graphviz package. Although this software is not specific to heat exchanger networks, the resulting graphical representation should be sufficient for understanding the results of evaluation and optimization.
Each stream in the network is traversed. The traversal of hot streams starts the root nodes for those streams. The traversal of cold streams starts from the leaf nodes so that the nodes in the stream are drawn in decreasing temperature order. This is consistent with a counter-current operation of the individual exchangers.
1:function traverse(n :: Node)2:print(" n$(n.id) ")3:if n.step isa Exchange4:if ishot(n)5:@printf " [label=\"X: %.3f Q\" shape=box]\n" n.step.Q6:else7:if n.step.Q > eps()8:@printf " [label=\"X: Q=%.1f\" shape=box]\n" n.step.Q9:else10:@printf " [label=\"X: Q=%.1f\" shape=box fontcolor=grey]\n" n.step.Q11:end12:end13:elseif n.step isa Utility14:if n.step.hex != nothing15:@printf(" [label=\"Utility\\nQ=%.1f\\nT=%.1f\\nA=%.2f\" shape=box color=%s]\n",16:n.in[1].stream.Q,17:n.in[1].stream.Tout,18:n.step.hex.A,19:(ishot(n) ? "blue" : "red"))20:else21:@printf(" [label=\"Utility\\nQ=%.1f\\nT=%.1f\" shape=box color=%s fontcolor=grey]\n",22:n.in[1].stream.Q,23:n.in[1].stream.Tout,24:(ishot(n) ? "blue" : "red"))25:end26:elseif n.step isa Inlet27:@printf " [label=\"Q=%.1f\\nT=%.1f\" shape=plaintext]\n" n.step.inlet.Q n.step.inlet.Tin28:elseif n.step isa Mix29:@printf " [label=\"mix\" shape=plaintext]\n"30:elseif n.step isa Split31:@printf(" [label=\"split: η=%.3f\\nmcp=%.3f/%.3f\" shape=plaintext]\n",32:n.step.η,33:n.step.η*n.in[1].stream.mcp,34:(1-n.step.η)*n.in[1].stream.mcp)35:else36:@printf " [label=\"\" shape=plaintext]\n"37:end38:# traverse this graph depth first39:if ishot(n)40:if n.out != nothing41:for e in n.out42:if e.to != nothing43:traverse(e.to)44:end45:end46:end47:else48:if n.in != nothing49:for e in n.in50:if e.from != nothing51:traverse(e.from)52:end53:end54:end55:end56:end57:function draw(problem :: HENS)58:network = problem.network59:# start of graphviz60:println("#+begin_src dot :file network.png :results file :eval no-export")61:println("graph network {62:overlap=scale63:nodesep=164:ranksep=1 ")65:# reset edges: flags, costs, designs66:map(e -> (e.traversed = false), network.edges)67:s = 1 # counter for streams68:# hot streams69:for n in network.inlets70:if ishot(n)71:println(" subgraph cluster$s { color=red; label=\"$(problem.streams[s])\"")72:s += 173:traverse(n)74:println(" }")75:end76:end77:# cold streams now78:for n in network.outlets79:if ! ishot(n)80:println(" subgraph cluster$s { color=blue; label=\"$(problem.streams[s])\"")81:s += 182:traverse(n)83:println(" }")84:end85:end86:# now connect the nodes, including exchanges87:for e in network.edges88:if e.from != nothing && e.to != nothing89:if ishot(e.from)90:print(" n$(e.from.id) -- n$(e.to.id)")91:else92:print(" n$(e.to.id) -- n$(e.from.id)")93:end94:if e.stream != nothing95:if e.stream.Q > eps()96:@printf(" [label=\"Q=%.1f\\nT=%.1f\"]\n",97:e.stream.Q, e.stream.Tin)98:else99:@printf(" [label=\"Q=%.1f\\nT=%.1f\" fontcolor=grey]\n",100:e.stream.Q, e.stream.Tin)101:end102:else103:println()104:end105:end106:end107:108:# finally, the exchanges between hot and cold109:for n in network.nodes110:if ishot(n)111:if n.step isa Exchange112:cold = n.step.match113:hex = cold.step.hex114:if hex != nothing115:@printf(" n%d:e -- n%d:e116:[label=\"A=%.2f\",117:style=dashed,118:constraint=false,119:weight=0]\n",120:n.id,121:n.step.match.id,122:hex.A)123:else124:@printf(" n%d:e -- n%d:e125:[label=\"A=0\",126:style=dashed,127:constraint=false,128:weight=0,129:color=grey,130:fontcolor=grey]\n",131:n.id,132:n.step.match.id)133:end134:end135:end136:end137:println("}")138:println("#+end_src")139:end
9. Acknowledgements
I would like to start by thanking those colleagues that enabled me to take a sabbatical leave to write this book, in alphabetical order: Solomon Bawa, Vivek Dua, Luca Mazzei, Alex Norori-McCormac, and Eva Sorensen.
I am indebted to Abdellah Salhi and Mr Daan van der Berg, as well as their researchers and students, for the many intense, productive, and very enjoyable discussions over the past years, usually involving a beer or two in very pleasant locations.
I would like to thank Steve Hurley who gave me permission to use his interp cubic interpolation code written in Julia. Although the actual case study that would have required this code was not included in the book in the end, the potential access to this code is gratefully acknowledged.
10. Bibliography
Footnotes:
An alternative possibly more efficient approach would be to use the Dictionaries.jl package.
Methods exist for analysing the size and shape of the feasible domain [Bates et al. 2007; Zilinskas et al. 2006].
I usually use the gnuplot tool for generating plots, as in the rest of the book, as gnuplot is, in my opinion, more customizable and powerful. For instance, the placement of the key, to avoid hiding some of the graphs, is easy to manipulate in gnuplot. Nevertheless, it is useful to illustrate a full Julia solution.
This was a conscious choice in the internal representation of the network. A different choice would have been to define an Inlet step explicitly.
This could be an issue in some cases. For instance, the temperature going below a particular value may result in a phase change in the stream, changing its behaviour. There could also be safety considerations as a result.
A fixed seed for the random number generator could be used to provide a more rigorous comparison but the aim of this book is not a rigorous assessment but an illustration of the codes and how they can be used.