OLD! - For current see BIOSCIENCES COURSE SITE
BIOL2007 - EVOLUTION OF GENETIC DIVERSITY
SO FAR WE HAVE:
a) Argued that the best definition of
evolution is change in gene frequencies.
b) Shown how selection can lead to fixation,
or replacement of an old allele by a new allele.
IN THE NEXT LECTURE:
Kevin will discuss how mutation
provides new raw material for evolution, in the form of new alleles.
HOWEVER:
Do genes always evolve until they become
fixed
(invariant in a population), or become immediately lost because they are
disfavoured? If so, most of the time, populations would be invariant and
no change would occur. However, in nature things are very different
...
IN FACT, THERE
IS PLENTY OF GENETIC VARIATION IN NATURAL POPULATIONS!
e.g. snail shell colour/banding, human
eye/hair colour, protein variation in just about everything, DNA variation
in absolutely everything
Understanding the evolution of this genetic
diversity Is a major goal of evolutionary genetics.
Possible explanations:
1) Selection
on its own may directly explain diversity of alleles. Here there
is direct selection for polymorphism and diversity.
a) heterozygous
advantage - selection for heterozygotes
b) diversifying
frequency-dependent selection - selection for rare forms when
their frequencies are low; ............OR:
2) Different forces may result in an equilibrium
(i.e. a balance between forces leading to a zero rate of evolution):
a) Mutation/selection
balance - disadvantageous mutations are not eliminated immediately,
especially if recessive. Mutation adds variants, and selection takes them
away. A balance between input and output results.
b) Drift/mutation
balance - some mutants will have little selection and might
drift about neutrally; drift tends to fix mutants, mutation to bring them
in. This is the neutral theory of evolution.
Here, the input of neutral mutations is balanced by genetic drift, which
tends to remove mutations, or more rarely such mutations may increase to
fix in the population. Because drift can be slow in large populations
relative to mutation, polymorphisms may frequently result (see later
in the course).
c) Migration/selection
balance - disadvantageous genes can often be maintained in a
population by migration from populations where the gene is favoured. Spatially
varying selection is common, for instance in the peppered moth (see later
in course).
HERE WE WILL DEAL
ONLY WITH:
(1a) heterozygote
advantage
[also (2a) mutation-selection
balance If we get around to it!!]
HETEROZYGOUS
ADVANTAGE
It is easy to see that heterozygous advantage
at a single locus with two alleles will lead to polymorphism:
AA
Aa aa
-------> !!FITTER!! <-------
Why? If you start with a pure population
of AA, and add a few Aa heterozygotes so that pA
is a little less than 1, Aa will do better than AA and a
will therefore increase. The population that is fixed for A is at
what is called an unstable equilibrium.
Similarly, if you start with aa common, rare
Aa heterozygotes
will do better, so A will this time increase. A population
with pA=0 is also at an unstable equilibrium.
Somewhere in the middle between the unstable equilibria p=0 and
p=1,
there will be a stable equilibrium.
BUT we can go further than this simple
verbal argument, and I am sure you will enjoy the maths, with me!
[In fact, almost the most interesting
parts of evolution are still mathematically intractable.
For instance, it is only possible to obtain solutions for evolution of
2-3 genes, compared to 1000s present in most genomes. So don't worry, the
maths doesn't get to hard! However, even if we can't get "analytical"
solutions
(for instance, equations for equilibria), we can still usually make approximations
(see Quantitative Characters), or obtain "numerical"solutions
(via computer simulations)].
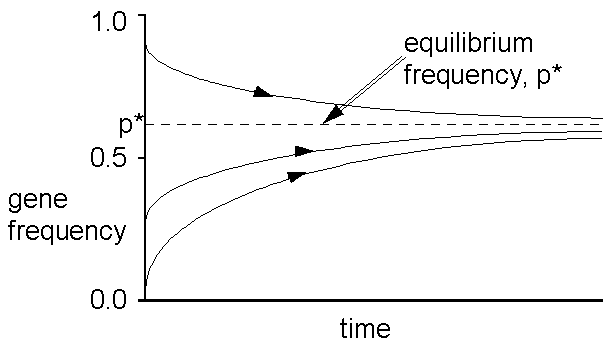
The above shows the time course of gene
frequency change under heterozygous advantage for different starting conditions.
Notice the stable equilibrium p*? (the gene frequency at which no
change results.) You can play with this on your own using the simulation
programs I have supplied. We can calculate this equlibrium (i.e.
when there is no further evolutionary change); using the symbols as before:
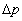 = 0 when pí - p = 0
= 0 when pí - p = 0
i.e. (change in gene freq.) = 0 when
(new gene freq.) - (old
gene freq.) = 0
Genotype AA Aa aa
Frequency p2 2pq q2
Fitnesses 1-s 1 1-t
In the next generation, once again we count
up the A and a alleles to get the frequency after selection,
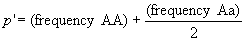 ,
as before
,
as before
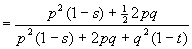 [ bottom line = the "mean fitness", as before]
[ bottom line = the "mean fitness", as before]
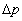 =
0 when
=
0 when 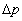 =
=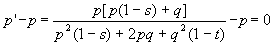 at equilibrium
at equilibrium
After a little manipulation,
this nasty looking piece of work can be shown to be equivalent to a much
simpler form:
pq(-sp + tq) = 0
Those of you who can remember back to your
GCSE algebra (all of you, I hope! If not, why not?), will immediately
realize that the above expression is true if one of three conditions are
met:
either p
= 0
or
q = 0
or
tq - sp = 0
The first two are fairly simple to understand.
The equation just says that if there are no a,
q = 0 and
the gene frequency remains fixed for A; if there are no A,
p
= 0, and the population remains fixed for a. This isn't really very
surprising, since with no variation, there can be no evolution. These
fixations are therefore called the trivial equilibria,
and as we have seen, they are unstable. Alternatively, the thing in brackets,
(-sp+tq) = 0, which is the same as saying tq = sp.
This third equation therefore gives the internal
or non-trivial equilibrium,
p*,
in which we are more interested because both A and a
are present; the population would be
polymorphic
(frequency > 0) in the population. Rearranging ...
tq* = sp*,
so t(1-p*) = sp*
therefore: t =
sp* + tp*, so (s+t)p*
= t
thus: .....
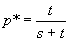 :
this is the polymorphic, or non-trivial equilibrium, which is stable
:
this is the polymorphic, or non-trivial equilibrium, which is stable
So, now if we know the selection pressures
s,t,
we can estimate the equilibrium frequency for heterozygous advantage; or
we can work the equation the other way round.
You could try out simulating heterozygous
advantage now in: natural
selection simulations. The programmes show whether the fitnesses
you enter produce directional selection or heterozygous advantage, and,
if the latter, they plot the value of the equilibrium p*
given above as a dotted line, so that you can see whether the gene frequencies
converge towards it.
Now what do you think happens when the
selection pressures s, and tare
negative?
In other words, if the homozygote fitnesses are
greater than the
heterozygote fitness (this is called heterozygote
disadvantage).
AA
Aa aa
<------ !!LESS FIT!! ------>
Here when we introduce a few Aa heterozygotes
to a pure population of AA, the AA do better, so the a
alleles are lost. A population fixed for A is at a stable equilibrium;
similarly, a population fixed for a is also stable.
Is there an internal equilibrium? Yes,
our formula for
p* shows it is again in the range 0 to 1; but this
time, the equilibrium only remains if the population starts at exactly
that frequency. Any slight perturbation, and it will diverge away from
the equilibrium, and eventually go to fixation at p=0 or p=1.
The equilibrium is here unstable,
in which case the only stable equlibria
are p=0 and p=1. This is quite an important case; because
it also represents
hybrid inviability;
this is common when we cross different species, and is possibly an important
cause of speciation.
You could try making s negative,
and t positive or vice-versa. The same p* is still an equilibrium,
but it isnít a case of heterozygous advantage or disadvantage, it is a
case like one we have dealt with already. Where is the "non-trivial" equilibrium
now? Calculate the relative fitnesses wAA,
wAa,
waa:
what kind of selection is this? Is the "internal" equilibrium sensible?
You could try out simulating these different fitnesses, heterozygous disadvantage,
heterozygous advantage, using real values in
natural
selection simulations, if you wanted.
Now letís try a real example, in humans:
malaria resistance.
ESTIMATING SELECTION
The data is electrophoretic forms of haemoglobin:
observations of beta-haemoglobin S (sickle-cell) and A (normal)
genotypes in a malaria-infested region of West Africa (simplified from
Cavalli Sforza & Bodmer 1971; available in Science
Lbrary: View 2007 Teaching Collection by going to eUCLid;
use Keyword, Basic Search, All Fields: 2007). We have seen
that one of the assumptions of Hardy-Weinberg equilibrium is that there
is no selection. If genotypic ratios deviate from Hardy-Weinberg,
we may suspect selection provided we can rule out inbreeding, migration
or other factors. Here we use a 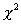 test to find whether there is evidence for deviation from Hardy-Weinberg:
test to find whether there is evidence for deviation from Hardy-Weinberg:
Testing whether
data conforms to Hardy-Weinberg ratios:
Table of genotype
frequency calculations:
Genotype AA AS SS TOTAL
O(bserved number) 25,374 5,482 67 30,923
Expected fraction 0.8266 0.1651 0.0082 0.999*
E(xpected number) (25,561.98) (5,106.03) (254.98) 30,922.99*
Calculations
of gene frequency and 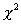 test:
test:
Gene frequency 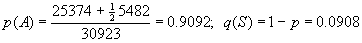
Assuming Hardy-Weinberg, the expected
genotype frequencies and expected numbers can now be calculated - see table
above. (*Calculator
notes)
Chi-square test: 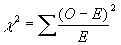 .
.
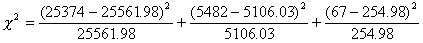
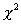 =
1.4 + 27.7 + 138.6 = 167.7
=
1.4 + 27.7 + 138.6 = 167.7
Although there are 3 classes of genotypes,
we lose degrees of freedom for any estimates we make from the data.
We lose 1 because we obtain the total from the data, and 1
because we estimate the gene frequency from the data, leaving 3-2=1
degree of freedom in this case.
Look for this value of 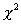 in your
in your 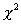 tables,
under
1 degree of freedom. You find that
tables,
under
1 degree of freedom. You find that 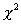 =167.7
greatly exceeds the value for P=0.001, which is
=167.7
greatly exceeds the value for P=0.001, which is 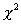 =10.83.
Therefore we can say that the probability of getting
a
=10.83.
Therefore we can say that the probability of getting
a 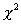 this big
in a large number of trials if the "null hypothesis" (i.e. Hardy-Weinberg
ratios) were true is much less than one in a thousand. In other
words, there is very strong evidence for a deviation from Hardy-Weinberg
-- we reject the null hypothesis.
this big
in a large number of trials if the "null hypothesis" (i.e. Hardy-Weinberg
ratios) were true is much less than one in a thousand. In other
words, there is very strong evidence for a deviation from Hardy-Weinberg
-- we reject the null hypothesis.
We usually say all this more briefly: "there
is a significant deviation from Hardy-Weinberg, P<0.001".
Estimating
selection coefficients:
If we know that the population is not inbreeding,
and we suspect selection against homozygotes; we can estimate the selection
based on the data we have just analysed:
Genotype AA AS SS
Work out fitnesses, O/E
0.99 1.07
0.26
now divide these through by by 1.07 to obtain
..
Relative fitnesses WAA WAS WSS
Values of fitnesses rel. to AS 0.92 1.00 0.24
Our selection model 1 - s 1 1 - t
Therefore the values of the selection coefficients
are estimated as: s = 0.08,
t = 0.76. (Check
the answer?)
TAKE HOME POINTS
-
There is much genetic
variation in nature
-
Polymorphisms within
populations be explained in a variety of ways:
-
Natural selection directly
favours polymorphism
-
heterozygote advantage
(done today)
-
frequency-dependent
selection
-
A balance of evolutionary
forces results in polymorphic equlibrium
-
a balance between mutation
and selection
-
a balance between mutation
and genetic drift (neutral evolution)
-
a balance between spatially
varying selection and migration
-
If we have information
about fitnesses for heterozygote advantage at a single locus with two alleles,
we can predict the polymorphic equilibrium frequency p*
-
In cases (such as in
sickle-cell haemoglobin alleles) where heterozygote advantage is suspected,
we can use deviations from Hardy-Weinberg in populations to estimate selection
pressures
FURTHER READING
FUTUYMA, DJ 1998.
Evolutionary Biology. Chapter 9 (pp. 231-247); Chapter 13 (pp. 376,
381-390).
Science Lbrary:
View 2007 Teaching Collection by going to eUCLid;
use Keyword, Basic Search, All Fields: 2007
Back to BIOL
2007 TIMETABLE
