| Research |
| Teaching |
| Publications |
| DensEl |
| ParaDens |
| Conquest |
| Links |
| Home |
Electrical conduction in nanoscale systems is a problem of increasing importance to understand, as the size of structures which can be fabricated decreases rapidly to the atomic scale. In collaboration with Andrew Horsfield (research fellow with the IRC in Nanotechnology), I have developed a formalism which allows us calculate the time evolution for the density matrix of a system, and from this find the current (both transient and steady-state). This work is being written up for Phys. Rev. Lett., and a preprint will be available soon.
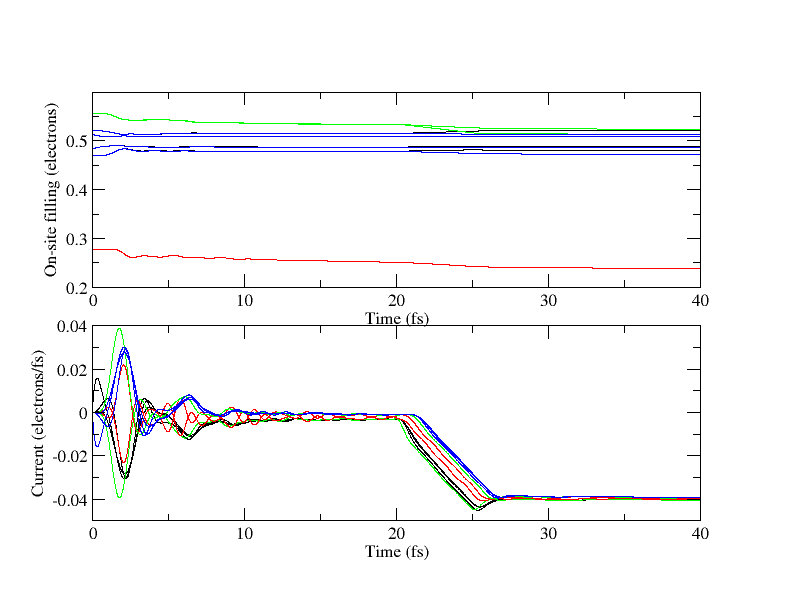
The graphs above show the current and on-site density matrix elements for a simple monatomic chain, with a barrier to conduction in the middle. There is no bias across the device for the first twenty femtoseconds, over which period the current converges towards zero. Between 20 and 25 fs, the bias is increased from 0 to -0.1V, and then held constant at that value. The current converges to a value which is in excellent agreement with steady-state Landauer formalism results.
In the top graph, red shows the atom forming the barrier, while green shows other atoms in the device, and black and blue show atoms in the left and right leads respectively. In the bottom graph, red shows the currents into and out of the barrier, green the currents into and out of the device, and black and blue currents in the left and right leads.
For examples of systems which might form, or support, wires whose conductance we'd want to calculate, see these other web pages of mine:
- Dangling bond wires on Si(001)
- Bi nanolines on Si(001)
- Many other systems, including conjugated polymers