


Next: Conclusions
Up: Classical Analysis
Previous: Vibrations of a solid
The hydrodynamic oscillations of a liquid drop, where the restoring force is
the surface tension of the liquid, have been treated by Chandrasekhar (1961).
For a drop with surface tension 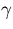 , density
, density 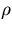 and radius a , the
period of oscillation is given by
and radius a , the
period of oscillation is given by
|
T = 2 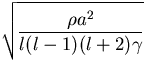 , ,
| (11)
|
where l is an integer greater than unity. We may gain some estimate of the
surface tension from March and
Tosi (1984), who show that for molten alkali halides a typical
value is of order
0.1 J m - 2. Thus for a sphere of radius
10 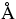 ,
the lowest-order oscillation has a period of approximately 17 ps . This
may be compared with the periods of the oscillations of the liquid drop in
the simulations, shown in region B of
figure 1, which are between 5 and 10 ps.
,
the lowest-order oscillation has a period of approximately 17 ps . This
may be compared with the periods of the oscillations of the liquid drop in
the simulations, shown in region B of
figure 1, which are between 5 and 10 ps.
The shape assumed by the surface of the sphere is given by
|
r(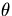 , ,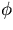 ) = a + BYl,m( ) = a + BYl,m(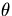 , ,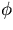 )exp(i )exp(i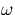 t) t)
| (12)
|
where B is the amplitude of the surface tension oscillation and Yl,m
is a spherical harmonic. The radial
and tangential velocities in this oscillation are
vr = i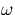 B B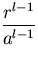 Yl,m( Yl,m(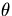 , ,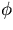 )exp(i )exp(i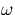 t) t)
|
|
| (13) |
vt = - i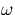 B B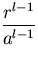 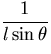 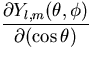 exp(i exp(i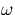 t) t)
|
|
| (14) |
from which we may evaluate the kinetic energy. In the fundamental (l = 2) mode this is
|
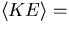 2B 2 2B 2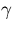 . .
| (15)
|
If we equate this energy to
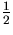 kT for
T = 2000 K , we find the amplitude to
be about
3
kT for
T = 2000 K , we find the amplitude to
be about
3 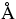 , and independent of the radius of the drop.
For a drop of radius
10
, and independent of the radius of the drop.
For a drop of radius
10 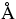 this amplitude is about one third of the drop radius.
This, of course, invalidates the perturbative approach by which the surface
tension oscillations were described, but it is consistent with the large
distortions of shape seen in the simulations of the molten LaF3 drops,
as shown in Figure 1.
this amplitude is about one third of the drop radius.
This, of course, invalidates the perturbative approach by which the surface
tension oscillations were described, but it is consistent with the large
distortions of shape seen in the simulations of the molten LaF3 drops,
as shown in Figure 1.



Next: Conclusions
Up: Classical Analysis
Previous: Vibrations of a solid
Tony Harker
4/23/1998
![]() , density
, density ![]() and radius a , the
period of oscillation is given by
and radius a , the
period of oscillation is given by
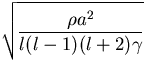 ,
,
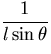
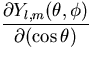 exp(i
exp(i