MATH0043 §2: Calculus of Variations

Many problems involve finding a function that maximizes or minimizes an integral expression.
One example is finding the curve giving the shortest distance between two points — a straight line, of course, in Cartesian geometry (but can you prove it?) but less obvious if the two points lie on a curved surface (the problem of finding geodesics.)
The mathematical techniques developed to solve this type of problem are collectively known as the calculus of variations.

Functionals and Extrema

Typical Problem: Consider a definite integral that depends on an unknown function $y(x)$, as well as its derivative $y'(x)=\frac{{\rm d} y}{{\rm d} x}$, \[%\renewcommand{\dx}{{\rm d}x} I(y) =\int_a^b~F(x,y,y')~{\rm d}x.\] A typical problem in the calculus of variations involve finding a particular function $y(x)$ to maximize or minimize the integral $I(y)$ subject to boundary conditions $y(a)=A$ and $y(b)=B$.

The integral $I(y)$ is an example of a functional, which (more generally) is a mapping from a set of allowable functions to the reals.

We say that $I(y)$ has an extremum when $I(y)$ takes its maximum or minimum value.

The Statement of an Example Problem

Consider the problem of finding the curve $y(x)$ of shortest length that connects the two points $(0,0)$ and $(1,1)$ in the plane. Letting ${\rm d}s$ be an element of arc length, the arc length of a curve $y(x)$ from $x=0$ to $x=1$ is $\int_0 ^1\; {\rm d}s$. We can use Pythagoras’ theorem to relate ${\rm d}s$ to ${\rm d}x$ and ${\rm d}y$: drawing a triangle with sides of length ${\rm d}x$ and ${\rm d}y$ at right angles to one another, the hypotenuse is $\approx {\rm d}s$ and so ${\rm d}s^2 = {\rm d}x^2 + {\rm d}y^2$ and $\mathrm{s} = \sqrt{\mathrm{d}x^2 + \mathrm{d}y^2} = \sqrt{1+ \left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2} \mathrm{d}x$. This means the arc length equals $\int_0^1 \sqrt{1+y'^2} {\rm d}x$.

The curve $y(x)$ we are looking for minimizes the functional\[I(y)= \int_0^1~ds = \int_0^1~(1+(y')^2)^{1/2} \; {\rm d}x~~~~\mbox{subject to boundary conditions}~~y(0)=0,~~y(1)=1\] which means that $I(y)$ has an extremum at $y(x)$. It seems obvious that the solution is $y(x)=x$, the straight line joining $(0,0)$ and $(1,1)$, but how do we prove this?

The Euler-Lagrange Equation, or Euler’s Equation

Let ${\rm C}^k[a,b]$ denote the set of continuous functions defined on the interval $a \le x \le b$ which have their first $k$-derivatives also continuous on $a \le x \le b$.

The proof to follow requires the integrand $F(x,y,y')$ to be twice differentiable with respect to each argument. What’s more, the methods that we use in this module to solve problems in the calculus of variations will only find those solutions which are in $C^2[a,b]$. More advanced techniques (i.e. beyond MATH0043) are designed to overcome this last restriction. This isn’t just a technicality: discontinuous extremal functions are very important in optimal control problems, which arise in engineering applications.

If $I(Y)$ is an extremum of the functional \[I(y)=\int_a^b~F(x,y,y')~{\rm d}x\] defined on all functions $y \in C^2[a,b]$ such that $y(a)=A, y(b)=B$, then $Y(x)$ satisfies the second order ordinary differential equation \[\label{ele} \frac{{\rm d}}{{\rm d} x}\left( \frac{\partial F}{\partial y'} \right)- \frac{\partial F}{\partial y} = 0.\]

Equation ([ele]) is the Euler-Lagrange equation, or sometimes just Euler’s equation.

You might be wondering what $\frac{\partial F}{\partial y'}$ is suppose to mean: how can we differentiate with respect to a derivative? Think of it like this: $F$ is given to you as a function of three variables, say $F(u,v,w)$, and when we evaluate the functional $I$ we plug in $x, y(x), y'(x)$ for $u,v,w$ and then integrate. The derivative $\frac{\partial F}{\partial y'}$ is just the partial derivative of $F$ with respect to its second variable $v$. In other words, to find $\frac{\partial F}{\partial y'}$, just pretend $y'$ is a variable.

Equally, there’s an important difference between $\frac{{\rm d} F}{{\rm d} x}$ and $\frac{\partial F}{\partial x}$. The former is the derivative of $F$ with respect to $x$, taking into account the fact that $y= y(x)$ and $y'= y'(x)$ are functions of $x$ too. The latter is the partial derivative of $F$ with respect to its first variable, so it’s found by differentiating $F$ with respect to $x$ and pretending that $y$ and $y'$ are just variables and do not depend on $x$. Hopefully the next example makes this clear:

Let $F(x,y,y') = 2x + xyy' + y'^2 + y$. Then \[\begin{aligned} \frac{\partial F}{\partial y'} &= xy + 2y' \\ \frac{{\rm d}}{{\rm d} x}\left( \frac{\partial F}{\partial y'}\right) &= y + xy' + 2{y'}' \\ \frac{\partial F}{\partial y} &= xy' + 1\\ \frac{\partial F}{\partial x} &= 2+yy'\\ \frac{{\rm d} F}{{\rm d} x} &= 2 + y y' + xy\prime ^2 + xyy\prime \prime + 2y\prime\prime y\prime + {y\prime}\end{aligned}\] and the Euler–Lagrange equation is \[y+xy'+2{y'} ' = xy'+1 \qedhere\]

$Y$ satisfying the Euler–Lagrange equation is a necessary, but not sufficient, condition for $I(Y)$ to be an extremum. In other words, a function $Y(x)$ may satisfy the Euler–Lagrange equation even when $I(Y)$ is not an extremum.

Consider functions $Y_\epsilon(x)$ of the form \[Y_\epsilon(x) = Y(x) + \epsilon \eta(x)\] where $\eta(x)\in C^2[a,b]$ satisfies $\eta(a)=\eta(b)=0$, so that $Y_\epsilon(a)=A$ and $Y_\epsilon(b)=B$, i.e. $Y_\epsilon$ still satisfies the boundary conditions. Informally, $Y_\epsilon$ is a function which satisfies our boundary conditions and which is ‘near to’ $Y$ when $\epsilon$ is small.¹ $I(Y_\epsilon)$ depends on the value of $\epsilon$, and we write $I[\epsilon]$ for the value of $I(Y_\epsilon)$: \[I[\epsilon]= \int^b_a ~F(x,Y_\epsilon, Y_\epsilon')~{\rm d}x.\] When $\epsilon = 0$, the function $I[\epsilon]$ has an extremum and so \[\frac{{\rm d}I}{{\rm d}\epsilon} = 0~~~~\mbox{when}~~~~\epsilon=0.\] We can compute the derivative $\frac{{\rm d}I}{{\rm d}\epsilon}$ by differentiating under the integral sign: \[\frac{{\rm d}I}{{\rm d}\epsilon}= \frac{{\rm d}}{{\rm d}\epsilon}\int^b_a F(x,Y_\epsilon, Y_\epsilon')~{\rm d}x = \int^b_a \frac{{\rm d}F}{{\rm d} \epsilon}(x,Y_\epsilon, Y_\epsilon')~{\rm d}x\] We now use the multivariable chain rule to differentiate $F$ with respect to $\epsilon$. For a general three-variable function $F(u(\epsilon), v(\epsilon),w(\epsilon))$ whose three arguments depend on $\epsilon$, the chain rule tells us that \[\frac{{\rm d} F}{{\rm d} \epsilon}= \frac{\partial F}{\partial u}\frac{{\rm d} u}{{\rm d} \epsilon} + \frac{\partial F}{\partial v}\frac{{\rm d} v}{{\rm d} \epsilon} + \frac{\partial F}{\partial w}\frac{{\rm d} w}{{\rm d} \epsilon}.\] In our case, the first argument $x$ is independent of $\epsilon$, so $\frac{{\rm d} x}{{\rm d} \epsilon}= 0$, and since $Y_\epsilon = Y+\epsilon \eta$ we have $\frac{{\rm d} Y_\epsilon}{{\rm d} \epsilon} = \eta$ and $\frac{{\rm d} Y_\epsilon'}{{\rm d} \epsilon} = \eta'$. Therefore \[\frac{{\rm d} F}{{\rm d} \epsilon} (x,Y_\epsilon,Y_\epsilon') = \frac{\partial F}{\partial y} \, \eta(x) + \frac{\partial F}{\partial y'} \, \eta'(x).\] Recall that $\frac{{\rm d} I}{{\rm d} \epsilon}=0$ when $\epsilon = 0$. Since $Y_0 = Y$ and $Y_0' = Y'$, \[\label{eat} 0 = \int_a ^b \frac{\partial F}{\partial y}(x,Y,Y') \eta(x) + \frac{\partial F}{\partial y'}(x,Y,Y')\eta'(x) ~ {\rm d} x.\] Integrating the second term in ([eat]) by parts \[\int_a^b \frac{\partial F}{\partial y'}\eta'(x)~ {\rm d}x = \left[ \frac{\partial F}{\partial y'}\eta(x) \right]^b_a - \int_a^b \frac{{\rm d}}{{\rm d} x}\left( \frac{\partial F}{\partial y'} \right) \eta(x)~ {\rm d}x.\] The first term on the right hand side vanishes because $\eta(a)=\eta(b)=0$. Substituting the second term into ([eat]), \[\int^b_a \, \left( \frac{\partial F}{\partial y} - \frac{{\rm d}}{{\rm d} x} \frac{\partial F}{\partial y'}\right) \eta(x)~ {\rm d}x = 0.\] The equation above holds for any $\eta(x)\in C^2[a,b]$ satisfying $\eta(a)=\eta(b)=0$, so the fundamental lemma of calculus of variations (explained on the next page) tells us that $Y(x)$ satisfies \[\frac{{\rm d}}{{\rm d} x}\left( \frac{\partial F}{\partial y'}\right)-\frac{\partial F}{\partial y} =0.\qedhere\]

A solution of the Euler-Lagrange equation is called an extremal of the functional.²

Find an extremal $y(x)$ of the functional \[I(y)= \int_0^1 (y'-y)^2 ~{\rm d}x, ~~~~~~y(0)=0,~y(1)=2,~~~~\left[ \mbox{Answer:} ~~ y(x)=2 \frac{\sinh{x}}{\sinh{1}} \right]. \qedhere\]

By considering $y+g$, where $y$ is the solution from exercise 1 and $g(x)$ is a variation in $y(x)$ satisfying $g(0)=g(1)=0$, and then considering $I(y+g)$, show explicitly that $y(x)$ minimizes $I(y)$ in Exercise 1 above. (Hint: use integration by parts, and the Euler–Lagrange equation satisfied by $y(x)$ to simplify the expression for $I(y+g)$).

Prove that the straight line $y=x$ is the curve giving the shortest distance between the points $(0,0)$ and $(1,1)$.

Find an extremal function of \[I[y]= \int_1^2 x^2(y')^2+y ~{\rm d}x, ~~~~~~y(1)=1,~y(2)=1,~~~~\left[ \mbox{Answer:}~~ y(x)=\frac{1}{2}\ln{x}+\frac{\ln{2}}{x}+1-\ln{2} \right].\]

MATH0043 Handout: Fundamental lemma of the calculus of variations

In the proof of the Euler-Lagrange equation, the final step invokes a lemma known as the fundamental lemma of the calculus of variations (FLCV).

[flcv] (FLCV). Let $y(x)$ be continuous on $[a,b]$, and suppose that for all $\eta(x) \in C^2[a,b]$ such that $\eta(a)=\eta(b)=0$ we have \[\int_a^b ~y(x)\eta(x)~{\rm d}x =0.\] Then $y(x)=0$ for all $a \le x \le b$.

Here is a sketch of the proof. Suppose, for a contradiction, that for some $a < \alpha < b$ we have $y(\alpha)>0$ (the case when $\alpha=a$ or $\alpha = b$ can be done similarly, but let’s keep it simple). Because $y$ is continuous, $y(x)>0$ for all $x$ in some interval $(\alpha_0, \alpha_1)$ containing $\alpha$.

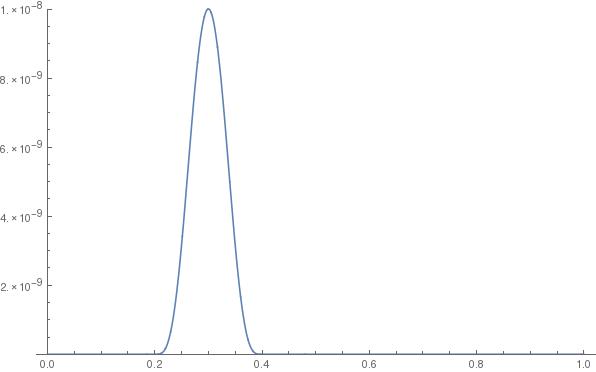
Consider the function $\eta : [a,b] \to \mathbb{R}$ defined by \[\eta(x) = \begin{cases} (x-\alpha_0)^4 (x-\alpha_1)^4 & \alpha_0 < x < \alpha_1 \\ 0 & \text{otherwise.} \end{cases}\] $\eta$ is in $C^2[a,b]$ — it’s difficult to give a formal proof without using a formal definition of continuity and differentiability, but hopefully the following plot shows what is going on:

By hypothesis, $\int_0^1 y(x)\eta(x)\;{\rm d}x= 0$. But $y(x)\eta(x)$ is continuous, zero outside $(\alpha_0, \alpha_1)$, and strictly positive for all $x \in (\alpha_0, \alpha_1)$. A strictly positive continuous function on an interval like this has a strictly positive integral, so this is a contradiction. Similarly we can show $y(x)$ never takes values $<0$, so it is zero everywhere on $[a,b]$.

The Brachistochrone

A classic example of the calculus of variations is to find the brachistochrone, defined as that smooth curve joining two points A and B (not underneath one another) along which a particle will slide from A to B under gravity in the fastest possible time.

Using the coordinate system illustrated, we can use conservation of energy to obtain the velocity $v$ of the particle as it makes its descent \[\frac{1}{2} m v^2 = mgx\] so that \[v = \sqrt{2gx}.\] Noting also that distance $s$ along the curve $s$ satisfies $ds^2=dx^2+dy^2$, we can express the time $T(y)$ taken for the particle to descend along the curve $y=y(x)$ as a functional: \[T(y)=\int^B_A \, dt = \int^B_A \, \frac{ds}{ds/dt} = \int^B_A \, \frac{ds}{v} = \int^h_0 \, \frac{\sqrt{1+(y')^2}}{\sqrt{2gx}}\, {\rm d}x, ~~~\mbox{subject to}~~~y(0)=0,~y(h)=a.\] The brachistochrone is an extremal of this functional, and so it satisfies the Euler-Lagrange equation \[\frac{d}{dx} \left( \frac{y'}{\sqrt{2gx(1+(y')^2)}} \right)=0,~~~y(0)=0,~y(h)=a.\] Integrating this, we get \[\frac{y'}{\sqrt{2gx(1+(y')^2)}}=c\] where $c$ is a constant, and rearranging \[y'=\frac{dy}{dx}=\frac{\sqrt{x}}{\sqrt{\alpha-x}}, ~~~~\mbox{with}~~\alpha=\frac{1}{2gc^2}.\] We can integrate this equation using the substitution $x=\alpha \sin^2{\theta}$ to obtain \[y= \int \, \frac{\sqrt{x}}{\sqrt{\alpha-x}} \, {\rm d}x= \int \, \frac{\sin{\theta}}{\cos{\theta}} \; 2 \alpha \sin{\theta} \cos{\theta}\, d\theta = \int \, \alpha (1-\cos{2\theta}) \, d\theta = \frac{\alpha}{2} (2\theta-\sin{2\theta})+k.\] Substituting back for $x$, and using $y(0)=0$ to set $k=0$, we obtain \[y(x)= \alpha \sin^{-1}{\left(\sqrt{\frac{x}{\alpha}}\right)}-\sqrt{x}\sqrt{\alpha-x}.\]

The constant $\alpha$ is determined implicitly by the remaining boundary condition $y(h)=a$. The equation of the cycloid is often given in the following parametric form (which can be obtained from the substitution in the integral) \[\begin{aligned} x(\theta) & = & \frac{\alpha}{2}(1-\cos{2\theta}) \\ y(\theta) & = & \frac{\alpha}{2}(2\theta-\sin{2\theta}) \end{aligned}\] and can be constructed by following the locus of the initial point of contact when a circle of radius $\alpha/2$ is rolled (an angle $2\theta$) along a straight line.

Functionals leading to special cases

When the integrand $F$ of the functional in our typical calculus of variations problem does not depend explicitly on $x$, for example if \[I(y) = \int_0 ^1 (y' - y)^2 {\rm d}x,\] extremals satisfy an equation called the Beltrami identity which can be easier to solve than the Euler–Lagrange equation.

If $I(Y)$ is an extremum of the functional \[I=\int_a^b~F(y,y')~{\rm d}x\] defined on all functions $y \in C^2[a,b]$ such that $y(a)=A,y(b)=B$ then $Y(x)$ satisfies \[\label{belt} F - y' \frac{\partial F}{\partial y'} = C\] for some constant $C$.

Consider \[\label{dif} \frac{{\rm d}}{{\rm d} x}\left( F- y'\frac{\partial F}{\partial y'} \right) = \frac{{\rm d} F}{{\rm d} x}-{y'}' \frac{\partial F}{\partial y'} -y' \frac{{\rm d}}{{\rm d} x} \left( \frac{\partial F}{\partial y'} \right).\] Using the chain rule to find the $x$-derivative of $F(y(x),y'(x))$ gives \[\frac{{\rm d} F}{{\rm d} x}= y' \frac{\partial F}{\partial y} + {y'}' \frac{\partial F}{\partial y'}\] so that ([dif]) is equal to \[y' \frac{\partial F}{\partial y} + y\prime\prime \frac{\partial F}{\partial y'} - y^{\prime \prime} \frac{\partial F}{\partial y'} - y' \frac{{\rm d}}{{\rm d} x}\frac{\partial F}{\partial y'} = y' \left( \frac{\partial F}{\partial y} - \frac{{\rm d}}{{\rm d} x}\frac{\partial F}{\partial y'} \right)\] Since $Y$ is an extremal, it is a solution of the Euler–Lagrange equation and so this is zero for $y=Y$. If something has zero derivative it is a constant, so $Y$ is a solution of \[F - y' \frac{\partial F}{\partial y'}= C\] for some constant $C$.

(Exercise 1 revisited): Use the Beltrami identity to find an extremal of \[I(y)= \int_0^1 (y'-y)^2 ~{\rm d}x, ~~~~~~y(0)=0,~y(1)=2,\] Answer: \[y=f(x)=2 \frac{\sinh{x}}{\sinh{1}}\] (again).

Isoperimetric Problems

So far we have dealt with boundary conditions of the form $y(a)=A,y(b)=B$ or $y(a)=A, y'(b)=B$. For some problems the natural boundary conditions are expressed using an integral. The standard example is Dido’s problem³: if you have a piece of rope with a fixed length, what shape should you make with it in order to enclose the largest possible area? Here we are trying to choose a function $y$ to maximise an integral $I(y)$ giving the area enclosed by $y$, but the fixed length constraint is also expressed in terms of an integral involving $y$. This kind of problem, where we seek an extremal of some function subject to ‘ordinary’ boundary conditions and also an integral constraint, is called an isoperimetric problem.

A typical isoperimetric problem is to find an extremum of \[I(y)=\int_a^b~F(x,y,y')~{\rm d}x,~~~\mbox{subject to}~y(a)=A,~y(b)=B, J(y)=\int_a^b~G(x,y,y')~{\rm d}x=L.\] The condition $J(y)=L$ is called the integral constraint.

In the notation above, if $I(Y)$ is an extremum of $I$ subject to $J(y)=L$, then $Y$ is an extremal of \[K(y)= \int_a^b~F(x,y,y')+ \lambda G(x,y,y') \;{\rm d}x\] for some constant $\lambda$.

You will need to know about Lagrange multipliers to understand this proof: see the handout on moodle (the constant $\lambda$ will turn out to be a Lagrange multiplier).

Suppose $I(Y)$ is a maximum or minimum subject to $J(y)=L$, and consider the two-parameter family of functions given by \[Y(x) + \epsilon \eta(x) + \delta \zeta(x)\] where $\epsilon$ and $\delta$ are constants and $\eta(x)$ and $\zeta(x)$ are twice differentiable functions such that $\eta(a)=\zeta(a)=\eta(b)=\zeta(b)=0$, with $\zeta$ chosen so that $Y+\epsilon \eta + \delta \zeta$ obeys the integral constraint.

Consider the functions of two variables \[I[\epsilon, \delta] = \int_a^b F(x,Y+\epsilon \eta + \delta \zeta,Y'+\epsilon \eta' +\delta \zeta') \,{\rm d}x, ~~ J[\epsilon, \delta] = \int_a^b G(x,Y+\epsilon \eta + \delta \zeta,Y'+\epsilon \eta' +\delta \zeta') \, {\rm d}x.\] Because $I$ has a maximum or minimum at $Y(x)$ subject to $J=L$, at the point $(\epsilon,\delta)$=$(0,0)$ our function $I[\epsilon, \delta]$ takes an extreme value subject to $J[\epsilon, \delta]=L$.

It follows from the theory of Lagrange multipliers that a necessary condition for a function $I[\epsilon, \delta]$ of two variables subject to a constraint $J[\epsilon, \delta]=L$ to take an extreme value at $(0,0)$ is that there is a constant $\lambda$ (called the Lagrange multiplier) such that \[\begin{aligned} \frac{\partial I}{\partial \epsilon} + \lambda \frac{\partial J}{\partial \epsilon} &= 0 \\ \frac{\partial I}{\partial \delta} + \lambda \frac{\partial J}{\partial \delta} &= 0 \end{aligned}\] at the point $\epsilon = \delta = 0$. Calculating the $\epsilon$ derivative, \[\begin{aligned} \frac{\partial I}{\partial \epsilon} [\epsilon,\delta] + \lambda \frac{\partial J}{\partial \epsilon}[\epsilon, \delta] & = & \int_a^b \frac{\partial}{\partial \epsilon} \left( F(x,Y+\epsilon \eta + \delta \zeta,Y'+\epsilon \eta' +\delta \zeta') +\lambda G(x,Y+\epsilon \eta + \delta \zeta,Y'+\epsilon \eta' +\delta \zeta') \right) \,{\rm d}x \\ & = & \int_a^b \eta \frac{\partial}{\partial y}\left( F+\lambda G \right) + \eta' \frac{\partial}{\partial y'} \left( F+\lambda G \right)\,{\rm d}x ~~~~~~~~~~~~~~~\mbox{(chain rule)} \\ & = & \int_a^b \eta \left( \frac{\partial}{\partial y}\left( F+\lambda G \right) - \frac{{\rm d}}{{\rm d} x}\left( \frac{\partial}{\partial y'} \left( F+\lambda G \right) \right) \right) \,{\rm d}x ~~~~\mbox{(integration by parts)} \\ & & \\ & = & 0~~~~~{\mbox{when $\epsilon=\delta=0$, no matter what $\eta$ is.}} \end{aligned}\] Since this holds for any $\eta$, by the FLCV (Lemma [flcv]) we get \[(F_y + \lambda G_y) ( x,Y,Y') + \frac{{\rm d}}{{\rm d} x}(F_{y'} + \lambda G_{y'}) (x,Y,Y') = 0\] which says that $Y$ is a solution of the Euler–Lagrange equation for $K$, as required.

Note that to complete the solution of the problem, the initially unknown multiplier $\lambda$ must be determined at the end using the constraint $J(y)=L$.

Find an extremal of the functional \[I(y) = \int_0^1 (y')^2~{\rm d}x, ~~~~~y(0)=y(1)=1,\] subject to the constraint that \[~~~~~J(y)=\int_0^1 y~{\rm d}x=2. ~~~~\left[ \mbox{Answer:}~~y=f(x)=-6\left(x-\frac{1}{2}\right)^2+\frac{5}{2}. \right]\]

(Sheep pen design problem): A fence of length $l$ must be attached to a straight wall at points A and B (a distance $a$ apart, where $a<l$) to form an enclosure. Show that the shape of the fence that maximizes the area enclosed is the arc of a circle, and write down (but do not try to solve) the equations that determine the circle’s radius and the location of its centre in terms of $a$ and $l$.