MATH0043 §2: Calculus of Variations
Contents
What is the Calculus of Variations?
Many problems involve finding a function that maximizes or minimizes an
integral expression.
One example is finding the curve giving the
shortest distance between two
points — a straight line, of course, in Cartesian geometry (but can you prove
it?) but less obvious if the two points lie on a curved
surface (the problem of finding geodesics.)
The mathematical techniques developed to solve this type of problem
are collectively known as the calculus of variations.
1 Functionals and Extrema
Typical Problem: Consider a definite integral that depends on an unknown function , as well as its derivative ,
A typical problem in the calculus of variations involve finding a particular function to maximize or minimize the integral subject to boundary conditions and .
Definition 1.
The integral is an example of a functional, which (more generally) is a mapping from a set of allowable functions to the reals.
We say that has an extremum when takes its maximum or minimum value.
2 The Statement of an Example Problem
Consider the problem of finding the curve of shortest length that connects the two points and in the plane. Letting be an element of arc length, the arc length of a curve from to is . We can use Pythagoras’ theorem to relate to and : drawing a triangle with sides of length and at right angles to one another, the hypotenuse is and so and . This means the arc length equals .
The curve we are looking for minimizes the functional
which means that has an extremum at . It seems obvious that the solution is , the straight line joining and , but how do we prove this?
3 The Euler-Lagrange Equation, or Euler’s Equation
Definition 2.
Let denote the set of continuous functions defined on the interval which have their first -derivatives also continuous on .
The proof to follow requires the integrand to be twice differentiable with respect to each argument. What’s more, the methods that we use in this module to solve problems in the calculus of variations will only find those solutions which are in . More advanced techniques (i.e. beyond MATH0043) are designed to overcome this last restriction. This isn’t just a technicality: discontinuous extremal functions are very important in optimal control problems, which arise in engineering applications.
Theorem 1.
If is an extremum of the functional
defined on all functions such that , then satisfies the second order ordinary differential equation
| (1) |
Definition 3.
Equation (1) is the Euler-Lagrange equation, or sometimes just Euler’s equation.
Warning 1.
You might be wondering what is suppose to mean: how can we differentiate with respect to a derivative? ††margin: \dbend Think of it like this: is given to you as a function of three variables, say , and when we evaluate the functional we plug in for and then integrate. The derivative is just the partial derivative of with respect to its second variable . In other words, to find , just pretend is a variable.
Equally, there’s an important difference between and . The former is the derivative of with respect to , taking into account the fact that and are functions of too. The latter is the partial derivative of with respect to its first variable, so it’s found by differentiating with respect to and pretending that and are just variables and do not depend on . Hopefully the next example makes this clear:
Example 1.
Let . Then
and the Euler–Lagrange equation is
Warning 2.
satisfying the Euler–Lagrange equation is a necessary, but not sufficient, condition for to be an extremum. ††margin: \dbendIn other words, a function may satisfy the Euler–Lagrange equation even when is not an extremum.
Proof.
Consider functions of the form
where satisfies , so that and , i.e. still satisfies the boundary conditions. Informally, is a function which satisfies our boundary conditions and which is ‘near to’ when is small.11 1 The function is known as the variation in . depends on the value of , and we write for the value of :
When , the function has an extremum and so
We can compute the derivative by differentiating under the integral sign:
We now use the multivariable chain rule to differentiate with respect to . For a general three-variable function whose three arguments depend on , the chain rule tells us that
In our case, the first argument is independent of , so , and since we have and . Therefore
Recall that when . Since and ,
| (2) |
Integrating the second term in (2) by parts
The first term on the right hand side vanishes because . Substituting the second term into (2),
The equation above holds for any satisfying , so the fundamental lemma of calculus of variations (explained on the next page) tells us that satisfies
Definition 4.
A solution of the Euler-Lagrange equation is called an extremal of the functional.22 2 Don’t confuse this with ‘extremum’. The terminology is standard, e.g. Gelfand and Fomin p.15, but can be confusing.
Exercise 1.
Find an extremal of the functional
Exercise 2.
By considering , where is the solution from exercise 1 and is a variation in satisfying , and then considering , show explicitly that minimizes in Exercise 1 above. (Hint: use integration by parts, and the Euler–Lagrange equation satisfied by to simplify the expression for ).
Exercise 3.
Prove that the straight line is the curve giving the shortest distance between the points and .
Exercise 4.
Find an extremal function of
MATH0043 Handout: Fundamental lemma of the calculus of variations
In the proof of the Euler-Lagrange equation, the final step invokes a lemma known as the fundamental lemma of the calculus of variations (FLCV).
Lemma 1.
(FLCV). Let be continuous on , and suppose that for all such that we have
Then for all .
Here is a sketch of the proof. Suppose, for a contradiction, that for some we have (the case when or can be done similarly, but let’s keep it simple). Because is continuous, for all in some interval containing .
Consider the function defined by
is in — it’s difficult to give a formal proof without using a formal definition of continuity and differentiability, but hopefully the following plot shows what is going on:
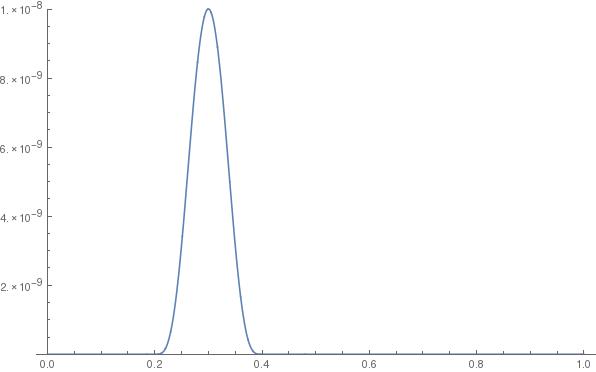
By hypothesis, . But is continuous, zero outside , and strictly positive for all . A strictly positive continuous function on an interval like this has a strictly positive integral, so this is a contradiction. Similarly we can show never takes values , so it is zero everywhere on .
4 The Brachistochrone
A classic example of the calculus of variations is to find the brachistochrone, defined as that smooth curve joining two points A and B (not underneath one another) along which a particle will slide from A to B under gravity in the fastest possible time.
Using the coordinate system illustrated, we can use conservation of energy to obtain the velocity of the particle as it makes its descent
so that
Noting also that distance along the curve satisfies , we can express the time taken for the particle to descend along the curve as a functional:
The brachistochrone is an extremal of this functional, and so it satisfies the Euler-Lagrange equation
Integrating this, we get
where is a constant, and rearranging
We can integrate this equation using the substitution to obtain
Substituting back for , and using to set , we obtain
Definition 5.
This curve is called a cycloid.
The constant is determined implicitly by the remaining boundary condition . The equation of the cycloid is often given in the following parametric form (which can be obtained from the substitution in the integral)
and can be constructed by following the locus of the initial point of contact when a circle of radius is rolled (an angle ) along a straight line.
5 Functionals leading to special cases
When the integrand of the functional in our typical calculus of variations problem does not depend explicitly on , for example if
extremals satisfy an equation called the Beltrami identity which can be easier to solve than the Euler–Lagrange equation.
Theorem 2.
If is an extremum of the functional
defined on all functions such that then satisfies
| (3) |
for some constant .
Definition 6.
(3) is called the Beltrami identity or Beltrami equation.
Proof.
Consider
| (4) |
Using the chain rule to find the -derivative of gives
so that (4) is equal to
Since is an extremal, it is a solution of the Euler–Lagrange equation and so this is zero for . If something has zero derivative it is a constant, so is a solution of
for some constant . ∎
Exercise 5.
(Exercise 1 revisited): Use the Beltrami identity to find an extremal of
Answer:
(again).
6 Isoperimetric Problems
So far we have dealt with boundary conditions of the form or . For some problems the natural boundary conditions are expressed using an integral. The standard example is Dido’s problem33 3 See Blåsjö - The Isoperimetric Problem for the history.: if you have a piece of rope with a fixed length, what shape should you make with it in order to enclose the largest possible area? Here we are trying to choose a function to maximise an integral giving the area enclosed by , but the fixed length constraint is also expressed in terms of an integral involving . This kind of problem, where we seek an extremal of some function subject to ‘ordinary’ boundary conditions and also an integral constraint, is called an isoperimetric problem.
A typical isoperimetric problem is to find an extremum of
The condition is called the integral constraint.
Theorem 3.
In the notation above, if is an extremum of subject to , then is an extremal of
for some constant .
You will need to know about Lagrange multipliers to understand this proof: see the handout on moodle (the constant will turn out to be a Lagrange multiplier).
Proof.
Suppose is a maximum or minimum subject to , and consider the two-parameter family of functions given by
where and are constants and and are twice differentiable functions such that , with chosen so that obeys the integral constraint.
Consider the functions of two variables
Because has a maximum or minimum at subject to , at the point = our function takes an extreme value subject to .
It follows from the theory of Lagrange multipliers that a necessary condition for a function of two variables subject to a constraint to take an extreme value at is that there is a constant (called the Lagrange multiplier) such that
at the point . Calculating the derivative,
Since this holds for any , by the FLCV (Lemma 1) we get
which says that is a solution of the Euler–Lagrange equation for , as required. ∎
Note that to complete the solution of the problem, the initially unknown multiplier must be determined at the end using the constraint .
Exercise 6.
Find an extremal of the functional
subject to the constraint that
Exercise 7.
(Sheep pen design problem): A fence of length must be attached to a straight wall at points A and B (a distance apart, where ) to form an enclosure. Show that the shape of the fence that maximizes the area enclosed is the arc of a circle, and write down (but do not try to solve) the equations that determine the circle’s radius and the location of its centre in terms of and .
Suggested reading
There are many introductory textbooks on the calculus of variations, but most of them go into far more mathematical detail that is required for MATH0043. If you’d like to know more of the theory, Gelfand and Fomin’s Calculus of Variations is available in the library. A less technical source is chapter 9 of Boas Mathematical Methods in the Physical Sciences. There are many short introductions to calculus of variations on the web, e.g.
- •
- •
- •
although all go into far more detail than we need in MATH0043. Lastly, as well as the moodle handout you may find
- •
useful as a refresher on Lagrange multipliers.