2 Sets and functions 2.3 Set algebra 2.5 Cartesian products

2.4 De Morgan’s laws

Take a look at this Venn diagram:

Figure 2.6: Venn diagram for the complement of the union of

A

and

B

You can see that the shaded area is exactly the area not in $A\cup B$ , so this is the Venn diagram for $(A\cup B)^{c}$ . Now consider the Venn diagrams for $A^{c}$ and $B^{c}$ :

Figure 2.7: Venn diagram for the complement of

A

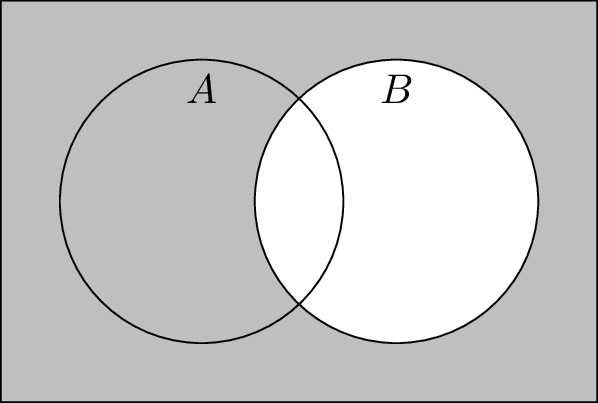
Refer to caption — Figure 2.8: Venn diagram for the complement of $B$

You can see from the diagrams that $A^{c}\cap B^{c}=(A\cup B)^{c}$ . This is a general and useful fact, one of De Morgan’s laws.

Theorem 2.4.1.

(De Morgan’s laws for sets). Let $A,B\subseteq\Omega$ and let $A^{c}$ and $B^{c}$ denote the complement with respect to $\Omega$ . Then

1.

$(A\cup B)^{c}=A^{c}\cap B^{c}$ , and
2.

$(A\cap B)^{c}=A^{c}\cup B^{c}$ .

Proof.

These follow from De Morgan’s laws in logic. The left hand side of the first of these is the set of all $x\in\Omega$ such that

\neg(x\in A\vee x\in B)

and the right hand side is the set of all $x\in\Omega$ such that

\neg(x\in A)\wedge\neg(x\in B).

Since $\neg(p\vee q)$ is logically equivalent to $(\neg p\wedge\neg q)$ (Theorem 1.6.3), the two sets have the same elements and so are equal. The second equality follows from the other logical De Morgan law. ∎

De Morgan’s laws also work for unions and intersections of more than two sets.

Theorem 2.4.2.

For any sets $A_{1},A_{2},\ldots$

1.

$(A_{1}\cup A_{2}\cup\cdots)^{c}=A_{1}^{c}\cap A_{2}^{c}\cap\cdots$ , and
2.

$(A_{1}\cap A_{2}\cap\cdots)^{c}=A_{1}^{c}\cup A_{2}^{c}\cup\cdots$