Popular Articles
- Uncertainty and nonlocality: a description of my paper with Stephanie Wehner, Science 2010.
- Quantum information can be negative: an accessible description of my paper with Horodecki and Winter in Nature.
- Sending quantum information down channels which cannot convey quantum information: A perspective in Science. A copy is available here.
- Quantum computing as free falling: A Science perspective on quantum computation as geometry. A copy is available here.
The second laws of quantum thermodynamics
Joint work with Fernando Brandao, Michal Horodecki, Nellie Ng & Stephanie Wehner
A copy of the paper, which appears this week in Proceedings of the National Academy of Sciences (PNAS)
will be available here (see also the arxiv version).
I've written a lay description of the research below. If you're already familiar with
thermodynamics and just want the more technical punchline, just jump to it after the steam engine
You're probably familiar with the second law of thermodynamics in one of its many forms:
Anything that can possibly go wrong, does.
"Happy families are all alike; every unhappy family is unhappy in its own way."
Shit happens
Because every day we feel the consequences of the second law. Even Homer Simpson has been known to admonish
his children: “In this house, we obey the laws of thermodamynics!" Not that Bart or Lisa would have much choice.
The second law of thermodynamics governs much of the world around us – it tells us that a hot cup of
tea in a cold room will not spontaneously heat up; it tells us that unless we are vigilant, our homes
will become untidy rather than tidy; it tells us how efficient the best engines can be and even helps us
distinguish the direction of time – we see vases shatter, but unless we watch movies backwards, never
see the time-reverse – a shattered vase reforming with just a nudge. The second law tells us that
order tends towards disorder, something we are all very familiar with -- trying to achieve a very
specific state of affairs can be very difficult, because there are many different ways things can go
wrong. Murphy's Law (anything that can go wrong, will go wrong), is a reasonable statement of the second
law of thermodynamics. As is its less precise version "Shit happens". More concretely, the second law
tells us that for isolated systems, the entropy, a measure of disorder, can only increase. I like to
think of the second law as constraining what can happen to a system -- left on its own, things don't get
more ordered.
But the laws of thermodynamics only apply to large classical objects, when many particles are involved.
What do the laws of thermodynamics look like for microscopic systems composed of just a few atoms?
That laws of thermodynamics might exist at the level of individual atoms was once thought to be an
oxymoron, since the laws were derived on the assumption that systems are composed of many atoms. Are there
even laws of thermodynamics at such a small scale? The question is becoming increasingly important, as
we probe the laws of physics at smaller and smaller scales.
Statistical laws apply when we consider large numbers. For example, imagine we toss a coin thousands of
times. In this case, we expect to see roughly equal numbers of heads as tails, while the chance that we
find all the coins landing heads is vanishingly small. If we imagine tossing a larger and larger number
of coins, the chance of having an anomalous coin tossing such as all tails goes to zero and our
confidence that we'll have roughly half heads, half tails, increases until we are virtually certain of
it. However, this is not true when tossing the coin just a few times. There's a reasonable chance we
will find all the coins landing tails. So, can we say anything reasonable in such a case? Similar
phenomena occur when considering systems made out of very few particles, instead of very many particles.
Can we make reasonable thermodynamical predictions, about systems which are only made up of a few
particles.
Surprisingly, the answer is yes, and the mathematical tools from a field known as quantum information
theory help us to understand the case when we don't have a large number of particles. What we find, is that not
only does the second law of thermodynamics hold for quantum systems, and those at the nano-scale, but
there are even additional second laws of thermodynamics. In fact, there is an entire family of second
laws. So, while Murphy's law is still true at the quantum scale -- things will still go wrong; the ways in
which things go wrong is further constrained by additional second laws.
Because remember, the second law is a constraint, telling us that a system can't get more ordered. These
additional second laws, can be thought of as saying that there are many different kinds of disorder at
small scales, and they all tend to increase as time goes on. What we find is a family of other measures
of disorder, all different to the standard entropy, and they must all increase.
This means that fundamentally, there are many second laws, all of which tell us that things become more
disordered, but each one constrains the way in which things become more disordered.
Why then does there
only appear to be one second law for large classical systems? That's because all the second laws,
although different at microscope scales, become similar at larger scales. At the scale of the ordinary
objects we are used to, all the quantum second laws are equal to the one we know and love.
What's more, it can sometimes happen that the traditional second law can appear to get violated –
quantum system can spontaneously become more ordered, while interacting with another system which barely
seems to change. That means some rooms in the quantum house may
spontaneously become much tidier, while others only become imperceptibly messier.
What do these additional second laws look like? Well, first let's get a bit more technically dirty.
If you already know your thermodynamics fairly well, this is a good point to join us. For those who've had enough,
here is a picture of Watt's steam engine. It's big enough that none of these additional second laws matter.
The first thing we want to do, is formulate the ordinary second law slightly differently.
Because actually,
the formulation -- that entropy increases for isolated systems, is not always the most useful one.
This is because there are many different definitions of entropy, and this formulation is not so interesting for some
types of entropy and sometimes violated for others.
For example, for isolated systems evolving under known dynamics, the Von Neumann or Shannon entropy
doesn't change at all, and so this formulation is boring, while for
the Boltzmann or coarse grained entropy, this version is sometimes violated.
The formulation which tends to be a bit more useful is that for an isolated system or one which is allowed to interact
with
a heat bath at temperature T, the free energy F=E-TS
can only go down. Here E is the total energy of the system, and S is its entropy. The free energy can be thought of as
the energy which is available to perform work (since some of the energy will be dissipated as heat). Now imagine we have a
system, and consider two possible states of that system (for example if our system is a vase, we could consider
two states of the vase, one in which it is unbroken, and the other when it's shattered). If we want to know whether
one state can evolve into another, we just need to check whether the free energy of the first state is higher than the
free energy of the second. If so, the initial state (the unbroken vase) can evolve into the target state (the shattered vase).
In fact, for macroscopic systems with short interactions, an initial state can evolve into a target state, if and only if
the free energy goes down in the process.
So what are the additional second laws for small systems? They just correspond to additional free energies.
For those that want to know there exact form, they're given by
If you find any of this interesting, then you might want to give the paper itself a try -- we've tried to write it in a way
which is reasonably accessible. In it, we also discuss how to reformulate the laws of thermodynamics in what is called
a resource theoretic framework. We also
prove something
which we call the zeroth law of quantum thermodynamics, which help defines the notion of temperature. We focus our discussion
on second laws for cyclic processes, which is how Clausius originally formulated the second law.
Of course no physical process is perfectly cyclic, so we need to consider approximately cyclic processes.
However, it turns out that there are different families of second laws depending on how
cyclic our processes are. But what do we
mean by approximately cyclic? You might thing that it's safe to demand that the process is close to perfectly cyclic, to
within some amount ε. But no matter how small you make ε, strange things can happen, and one can violate
the ordinary second law. It's a bit like being able to embezzle. Except instead of embezzling money from a bank,
we embezzle work from a single heat bath (something forbidden by the second law). The field of quantum thermodynamics seems to
contain some strange phenomena, and trying to understand them better is becoming an exciting ride.
--
-- Leo Tolstoy in Anna Karenina, almost 20 years before Boltzmann's Kinetic Theory of
Gases
-- ancient proverb

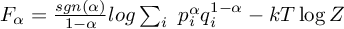 where Z is the partition function, k is Boltzmann's constant, p is the probability distribution of the state of interest, and q
is the distribution of the thermal state of the system. α runs from 0 to ∞. For α=1, this quantity is just equal
to the ordinary free energy, so one of these second laws correspond to the ordinary one. For α=0, the quantity is just
equal to the amount of work which can be distilled from the system, while for α→∞ we get the work required
to create the system from the thermal state. And as we increase the size of the system, it turns out that all these free
energies become approximately equal to the standard one F. Thus for larger, more complicated systems, the many second laws of
thermodynamics becomes just one. Things are so much simpler when they're much more complicated!
where Z is the partition function, k is Boltzmann's constant, p is the probability distribution of the state of interest, and q
is the distribution of the thermal state of the system. α runs from 0 to ∞. For α=1, this quantity is just equal
to the ordinary free energy, so one of these second laws correspond to the ordinary one. For α=0, the quantity is just
equal to the amount of work which can be distilled from the system, while for α→∞ we get the work required
to create the system from the thermal state. And as we increase the size of the system, it turns out that all these free
energies become approximately equal to the standard one F. Thus for larger, more complicated systems, the many second laws of
thermodynamics becomes just one. Things are so much simpler when they're much more complicated!