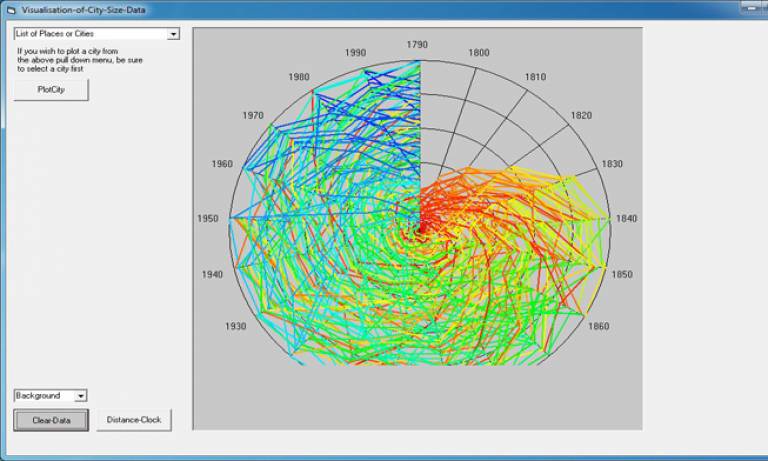
A rank clock is a device for visualising the changes over time in the ranked order of any set of objects where the ordering is usually from large to small.
The size of cities, of firms, the distribution of incomes, and such-like social and economic phenomena display highly ordered distributions. If you rank order these phenomena by size from largest to smallest, the objects follow a power law over much of their size range, or at least follow a log normal distribution which is a power law in the upper tail.
In fact for cities and other phenomena such as the distribution of word frequencies, George Kingsley Zipf as long ago as the 1930s characterised such distributions as characterising pure power laws in which the size of an object seemed to approximate the largest object in the set divided by the rank of the object in question. Such strict power laws in fact seem to be the exception rather than the rule but many such rank size distributions seem to follow such laws in their upper tail, and hence these are taken as signs of system stability, self-organisation and universality.
However despite the fact that such distributions are so regular even through time, when one examines how objects within these distributions change over time, it is quite clear that somehow these systems remain stable at the aggregate level but with objects which composes them shifting quite dramatically from time period to time period. The Rank Clock is a device that shows how such distributions change over time and it is a natural complement to the rank size distribution which is called a Zipf Plot.
We have developed a computer program for plotting these clocks and this can be downloaded in stripped down form with data for the top 100 cities in the US urban system for the decades from 1790 to 2000. We have also examined the UK urban system from 1901 to 2001, the World System from 430BCE to 2000, and the Ancient World System from 3700BCE to 1000BCE. All these examples show quite regular stability in rank size at the aggregate Zipf Plot level but much greater volatility in terms of the Rank Clocks and this in an of itself throws grave doubt on the issue of universality and regularity in such systems. Moreover it opens up once again the paradox of why systems show such regularity at the macro level when everything is changing at the micro level.
 Close
Close

