CASA Working Paper 204

Line Structure Interpretation of Networks: Relationships, Matrices and Properties

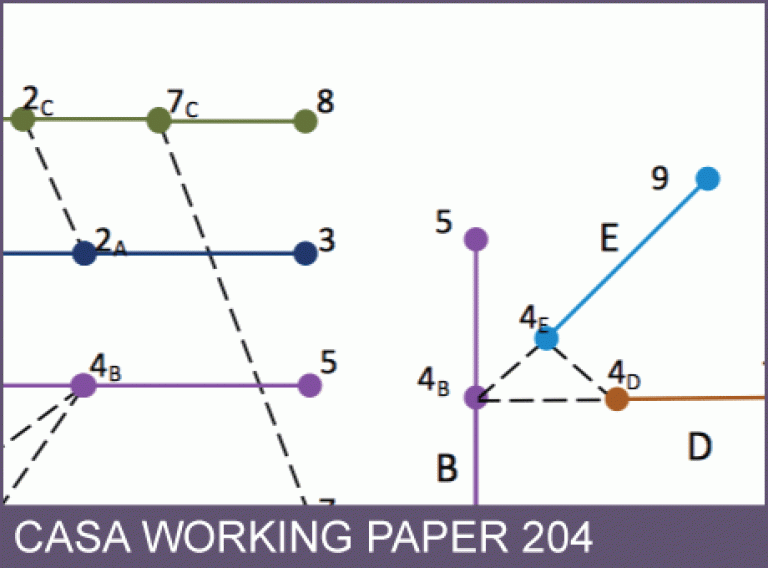
This working paper sets out an interpretation of the line structure as a device for representing network structure. First, the line structure S# is briefly introduced with reference to Euclidean and Cartesian geometry. Then its relation to the primal graph (G') and dual graph (G") are set out, demonstrated using an intermediate form, the hypergraph H#. A series of point matrices X and line matrices X for specifying the line structure are set out, from which line structural properties such as continuity and connectivity are derived.

Author: Stephen Marshall

Publication date: 19 August 2015
 

Download working paper 204 (file size 12.7Mb, PDF format)