CASA Working Paper 80

Distance in Space Syntax

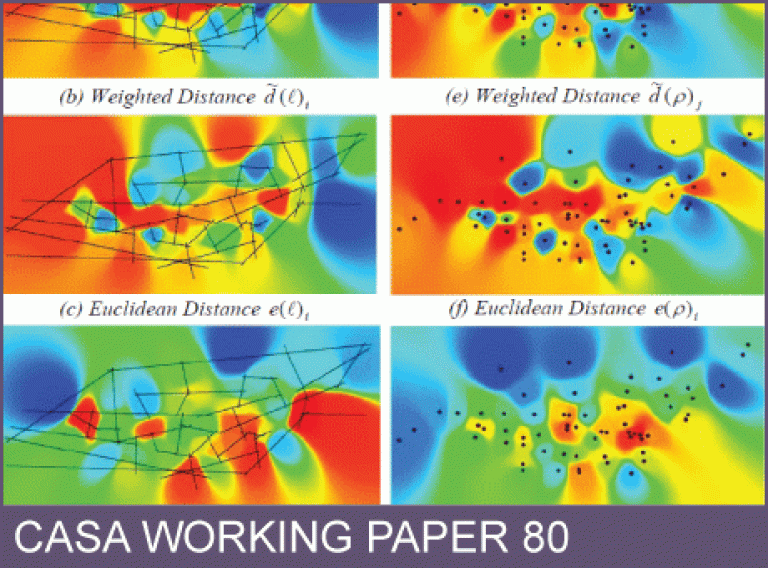
We explore ways of introducing Euclidean distances associated with street systems represented by axial lines into the two connectivity graphs based on points (or street junctions), and on lines (or streets), the so-called dual and primal representations of the space syntax problem. As the axial line is embedded in the connectivity graph between the points, for the dual problem the specification of Euclidean distance between points is relatively trivial but for the original syntax problem, this is problematic in that it requires us to find a unique point representation for each line.

The key is to find the centroids of the lines (of sight or unobstructed movement) between the points on each axial line, and then to use these to form a weighted centroid of centroids. The distances between axial lines which form paths through the connectivity graph between streets, are then computed using these centroids as starting points for each line and routing distance through the street junctions. There are many issues involving interpretation of these measures. It might be thought that the longer an axial line, the more important it is. But by giving an axial line distance, this suggests that this is a deterrence to interaction, as in spatial interaction theory, with longer axial lines being individually less important, notwithstanding the probability that they are better connected within the overall street system.

Clearly in many finer-scale morphologies, this assumption might not be tenable but the measures developed here can be easily adapted to various circumstances. What this focus on distance enables us to do is to treat a 'mixed syntax' problem where we are able to embed truly planar graphs into the axial map. This extends the technique to deal with systems not only comprising streets down which we can see, but also fixed rail lines, subway systems, footpaths and so on which currently are hard to handle in the traditional theory. We illustrate the extended theory for a pure syntax problem, the French village of Gassin, and a mixed syntax problem based on the grid of streets and underground railways in central Melbourne. In conclusion, we introduce the notion that proximity or adjacency at different orders might form more appropriate measures of syntax distance, the proximity of nodes to nodes and lines to lines in the dual and the primal being illustrated for both Gassin and central Melbourne.

This working paper is available as a PDF. The file size is 3.26MB.

Authors: Michael Batty

Publication Date: 1/4/2004

Download working paper No. 80.