Welcome to my website
My name is Belgin Seymenoğlu. I gained both my masters and PhD at UCL. More recently, I have been lecturing at the University of West London. Welcome to my academic webpage!
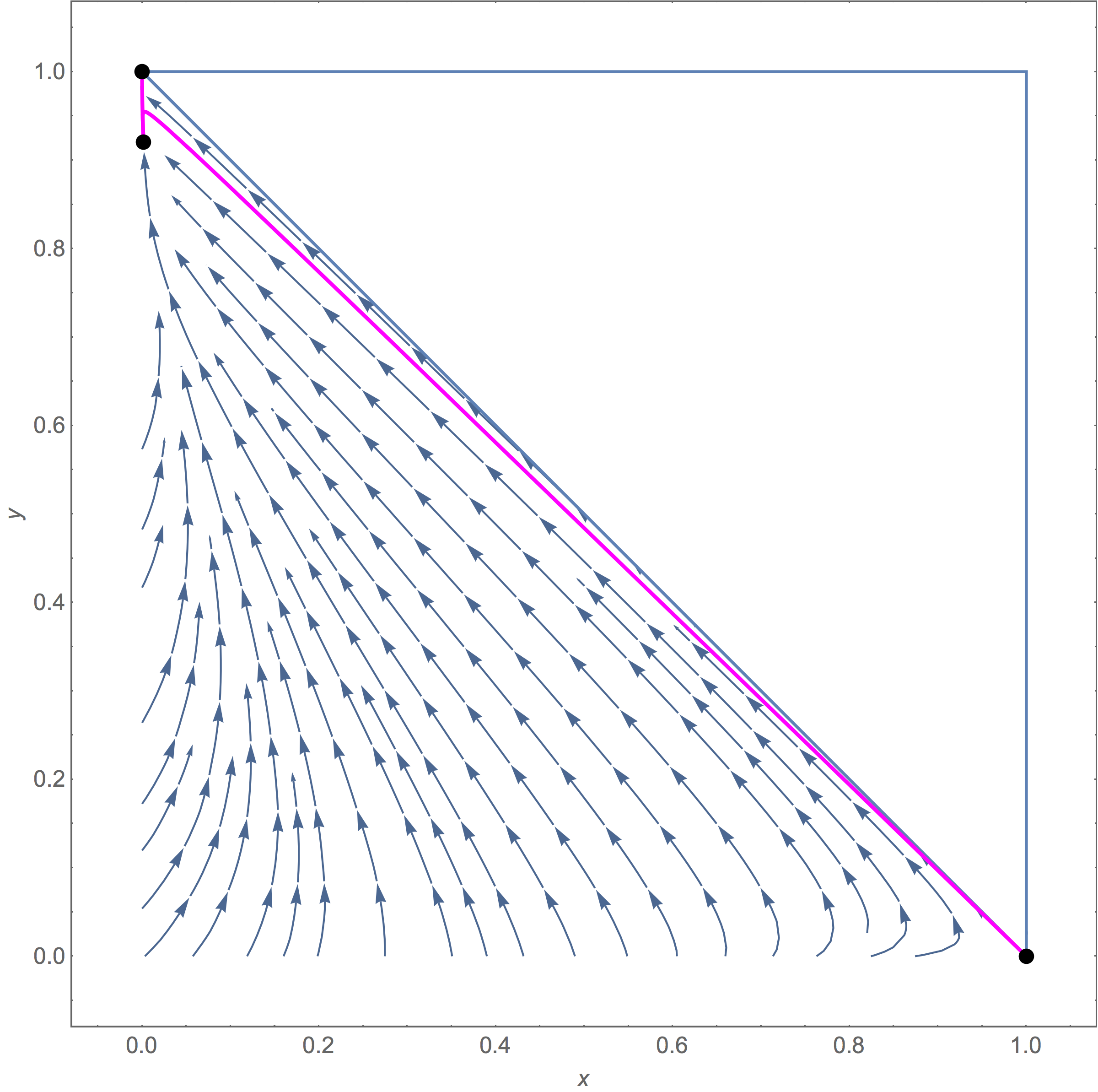
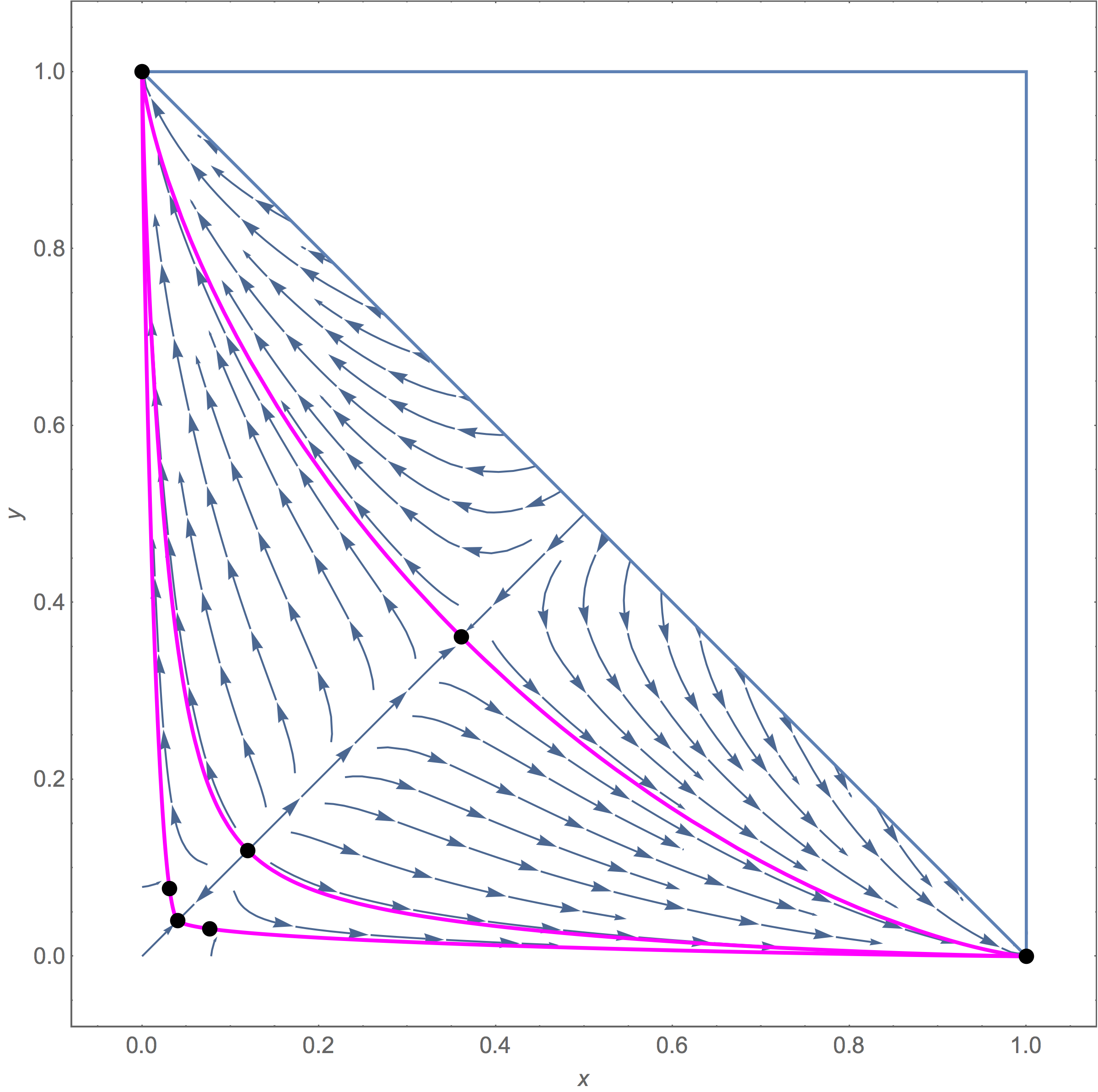
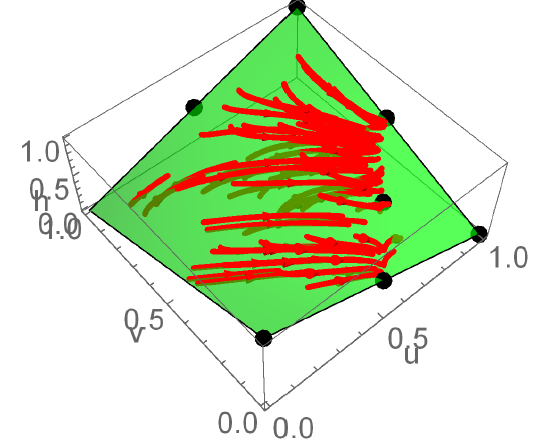
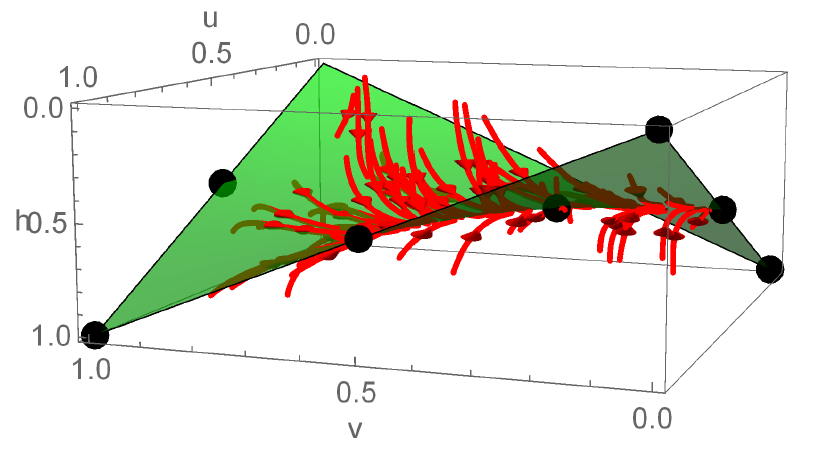
Many models in population genetics feature some form of convergence of the genetic state of the population, typically onto a so-called invariant manifold. This allows one to effectively reduce the the dynamical system to a problem with fewer dimensions, making it easier to investigate the stability of the fixed points in the model, as well as to predict the long-term evolution of the population.
In some models, an invariant manifold is known to exist, but with some very restrictive assumptions such as weak selection or additive fitnesses. My aim was to prove the existence of an invariant manifold for a handful of models in population genetics without relying on such assumptions, hence my results will be much more widely applicable.
I submitted my thesis in September 2018, and had my (five-hour!) viva two months later. My examiners were Rod Halburd and Josef Hofbauer. I am also turning parts of my thesis into papers.
Also, I gave a talk about my research in the Applied Mathematics Seminar at UCL last autumn! You can find the slides for the seminar here.
I investigated Cosserat models of elasticity for my MSci project. Unlike classical elastic models, which neglect the local structure of points in an elastic body, Cosserat models take into account both the change in position of points and the so-called microstructure, in which said points are allowed to undergo rigid rotations. In my project I analysed coupled elastic and rotational waves in the Cosserat model of Continuum mechanics and found some interacting soliton solutions. Moreover, I created the colourful animation below using Mathematica to visualise these waves. I have since written a paper about my project (see my list of publications).
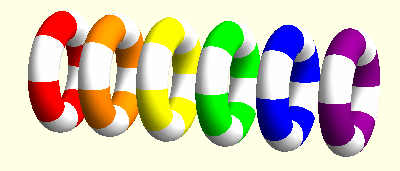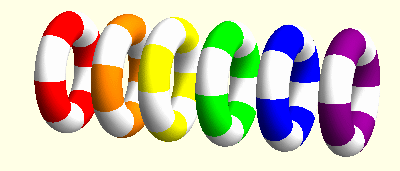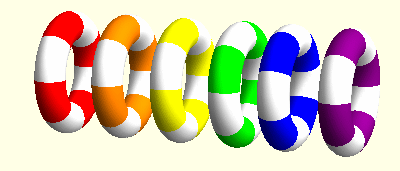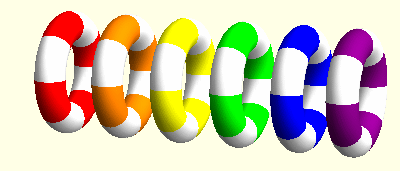
Since then, I have started comparing my Cosserat model with Skyrme's model from particle physics. The first step will be to put together a translation from Skyrme to Cosserat!
2018
- S. A. Baigent and B. Seymenoğlu, Competitive Selection-Recombination dynamics: A new approach to studying the Quasilinkage equilibrium manifold, submitted to Nonlinear Analysis: Real World Applications
- B. Seymenoğlu and S. A. Baigent, Nonmonotone invariant manifolds in the Nagylaki-Crow model, Nonlinear Analysis: Real World Applications, 41, 570-587, doi: 10.1016/j.nonrwa.2017.11.011
2016
University of West London
Over the past year, I taught four courses in Mathematics and Statistics at the University of West London:
I am presently teaching the second-year level course Real and Complex Analysis for the year at the University of West London. Lecture material will be posted here very soon!
I supervised six Foundation-level projects in Mathematics and Statistics in spring 2019. Teaching material will be posted here soon!
I am presently teaching the second-year level course Real and Complex Analysis for the year at the University of West London. Lecture material will be posted here soon!
I am presently teaching the Foundation level course Introduction to Statistics at the University of West London. Lecture material will be posted here soon!
UCL
My PhD office was Room M201 of the Kathleen Lonsdale Building. Instructions for finding this room are given here.
In the years 2015-2017 I taught the undergraduate course Mathematics for Engineers 1. All the lecture material for the course can be found here:
Admin
Lecture notes
Here is the complete set of lecture notes for the course.
Problem Sheets
- Sheet 1 (due October 14th)
- Sheet 2 (due October 21st)
- Sheet 3 (due October 28th)
- Sheet 4 (due November 4th)
- Sheet 5 (due November 18th)
- Sheet 6 (due November 25th)
- Sheet 7 (due December 2nd)
- Sheet 8 (due December 9th)
- Sheet 9 (not assessed)
Solutions to Problem Sheets
Handouts and links
I taught the following first-year tutor groups:
2016-2017
- MATH1301 others
2015-2016
- Mathematics with Economics
- Mathematics and Statistics
2014-2015
- Mathematics
- Mathematics and Statistics
I am a member of the team behind Chalkdust, a UK maths magazine for the mathematically curious.
This April the KLB had a re-opening ceremony, during which we demonstrated a pile of matchboxes that can learn how to play Noughts and Crosses to David Attenborough and others. We even got him to take away three issues of our magazine!