by Ted Honderich
-- The Determinism and Freedom Philosophy Website --
Causality is the relation between cause and effect, and causation either the causing of something or the relation between cause and effect. What follows here is an account of the fundamental relation or connection between an effect, say the windshield wipers starting to work in this car, and what precedes it. What precedes it, fundamentally, is a causal circumstance or causally sufficient condition. This includes a number of conditions, one of them usually called the cause of the effect, say flipping the switch.
The account below of the fundamental lawlike or 'whatever-else' connection between a causal circumstance and its effect is the third section of a book chapter, the first two sections having been about what causes and conditions are -- individual properties is the answer -- and about four unfundamental connections between the effect and the cause as well as other conditions. One of these four connections is the familiar one that if the cause hadn't happened, the effect wouldn't have happened either -- the cause was required for the effect.
The account of causality below rejects Hume's temptingly simple idea of the fifth and fundamental connection, between causal circumstance and effect -- that it is just that all things like the first are followed by things like the second. The account here, in line with Hume, does look directly at the subject-matter rather than approaching it by way of some enthusiasm or specialism, say probability-theory or the theory of possible worlds, as some philosophers do. The account isn't motivated, either, by a desire to have a story of causation that goes with free will and responsibility or anything else. It's not light reading -- much philosophy isn't. You need to concentrate a little to get the message, but there is no mystery in it.
The sections are as follows.
1.3 'IF A, EVEN IF X, THEN STILL B'
1.4 THE ANALYSIS OF CONDITIONAL STATEMENTS
1.5 CAUSAL VERSUS OTHER NOMIC CONNECTIONS
1.6 THE VIEW DEFENDED
1.6.1 Causation and Science
1.6.2 Specifying Causal Circumstances
1.6.3 Condition-Sets and Backgrounds
1.6.4 Causes as Merely Required for Effects
1.6.5 Non-Standard Causes
1.6.6 Probabilism
1.7 SUMMARY
For the details of the cited books and articles, go to References.
1.3 'IF A, EVEN IF X, THEN STILL B'
The fifth connection is different. To approach it informally, suppose that we spend time and arrive at a thorough understanding of the ordinary operation of this Citroen's windscreen wipers. We come to believe that whenever ten specified types of conditions obtain, including a flipping of the switch, there is the effect of the wipers' starting to work. What do we believe if on a certain occasion we have taken it that there exist conditions of exactly the ten types, including a flipping, but the wipers do not start? We may suppose that we are mistaken on this occasion in taking it that all the ten types of conditions do obtain. We may suppose, differently, that our prior thorough understanding of the ordinary operation of the wipers was not thorough enough. That is, there is an additional type of condition which obtains when the wipers start—not ten in all but eleven. More likely, we may suppose that we have not arrived at an exact specification of one or more of the ten. What is needed is not exactly a particular type of condition specified before the present occasion, but a slightly different one, which did indeed obtain previously when the wipers started.
What is common to these and related responses is that if we take the starting of the wipers to be an effect we believe at least that there is some type of circumstance which is uniformly connected with the wipers' starting. Whenever a circumstance of this kind exists, there also occurs a starting-to-work of the wipers. Certainly we do take any standard effect to be an instance of such a uniform connection. However, is this all that there is in the world, along these lines, to the connections between an effect and its causal circumstance?
Hume gave one of philosophy's most famous answers, an answer whose strength is owed to its great clarity and simplicity, when he said yes. (1888 (1739), pp. 73 ff.) To give the answer is to refuse to go far beyond what we already have, or have as implied, in connection (4). If the answer leads very naturally to the truth, it is nevertheless mistaken, as is shown by the philosophically familiar but evergreen fact that certain items constitute an instance of such a uniform connection or constant conjunction, but the second is not the effect of the first. Although each causal circumstance and effect, likewise, is an ' instance of such a uniform connection, that is not its unique nature.
Consider a particular day and the night that follows. The example is of course that of Hume's early critic Thomas Reid (1969 (1788) ), and has many counterparts, some of them being members of runs of total coincidences. Let us have in mind, only slightly less imprecisely, a period of light in London and thereabouts, that one I now call yesterday, and a following period of darkness, last night. We could of course give precise spatio-temporal specifications. It seems that if any two things whatever satisfy the Humean requirement, yesterday and last night do—all days are followed by nights. But yesterday and last night, however they are related, are not related as causal circumstance and effect. Yesterday did not cause last night. More must be true of any different pair of things which in fact are causal circumstance and effect.
There have been many attempts to save the Humean account, or some development of it. (Ayer, 1940, pp. 179 f.; Hempel and Oppenheim, 1953, pp.337ff.; Nagel, 1979, pp. 64 f.; Berofsky, 1971, pp. 203 f.; cf. Barman, 1986, Ch. 5; Honderich, 1991?) They cannot but strike one as unsuccessful, partly because ad hoc. The Humean view has persisted, among all those disinclined to mystery in connection with causation, not because of these defences, but for want of a ' satisfactory alternative. The alternatives have for the most part consisted in elusive doctrines of 'natural necessity', causal 'power', 'agency' or some kind of 'logical connection' and in inexplicit declarations of the reality of causal necessitation. Now there are superior alternatives, not at all of the unsatisfactory kinds. One of them, to my mind, gives an unfanciful, clear, and true view of the relation between causal circumstance and effect. This alternative view, a member of a small family of related although differing views, follows on naturally enough from a consideration of Hume's.
Why do we not take yesterday as the causal circumstance for last night? What do we take to be the difference between yesterday and last night, on the one hand, and, on the other, another instance of constant conjunction, the one comprising the true causal circumstance and last night? It is that we might, in other than merely a logical sense, have got yesterday but not last night. Certain other events or conditions might have occurred such that we got yesterday but not last night. One would have been the creation of a new light source, about as great as the sun. It is thus false that if certain other things had happened, although we got yesterday, we would still have got last night.
Compare what we take to be the true causal circumstance for last night, which we may label the solar conditions. They included, roughly speaking, the earth's London face being away from the sun for a time, the absence of any light source like that of the sun, in the right place at the right time, and conditions having to do with the behaviour of light. It is not true that certain other events or conditions might have occurred such that we got the solar conditions but not last night. If or since we had the solar conditions, even if certain other things had happened, we would still have got last night. This is indeed what distinguishes causal circumstances and effects (and nomic correlates) from other instances of constant conjunction. This, if it needs to be made more precise, is what we need to concentrate on, as some others have before, although without coming to the conclusion we shall reach. (Mill, 1961 (1843), Bk. 3, Ch. 5, s. 6; Ayer, 1963, 1963a, pp. 231-4; Goodman, 1954; Hospers, 1956; Downing, 1958-9, 1959, 1970; Honderich, 198 lb, pp. 421 f., 1982a, pp. 302-3)
Let us take the variable x to cover or range over certain conceivable events or conditions or whatever—in fact individual properties or sets . of them—which in fact did not occur. They are, we can as well say, certain conceivable changes in the universe, ways in which the universe might have been different. Let us contemplate, first, that they include all such changes save for the absence of cc or of e. They include all such changes save for logical excluders of cc or e. We can now contemplate that the relevant cc-e connection, when we suppose that cc caused e, can be stated in this way: If cc occurred, then even if x had occurred, e would still have occurred. That is on the right lines, of course, since certainly we do not suppose that e would have occurred even if either cc or e itself did not. However, it will not do. We regularly take it that a causal circumstance is linked by way of a causal chain or sequence to its effect. Without attempting a characterization of such sequences, let us suppose that a link k occurred in a causal sequence connecting cc with e. Clearly we do not believe that since cc occurred, e would still have as it did, even if k had been missing. We need to restrict x a bit more in order to express what we want.
What we come to is this. If cc was a causal circumstance for e, then
(5) If cc occurred, then even if there also occurred any change x logically consistent with cc and e, it was never the less the case that e occurred -- or, cc began and e ended a sequence of things such that it was true of each one and its immediate successor that if the first occurred, even if there also occurred any change x logically consistent with both, then the second also occurred. To speak differently, if e had not occurred, then even if there had also occurred any change x logically consistent with the absences of e and of cc, and consistent with the absences of links between cc and e, it would also have been the case that cc did not occur.
This fifth causal relation, like several to come, is stated by what we can call independent nomic conditional statements, or simply inde-pendent conditionals. Their truth, in brief, is independent of what else is true. Expressed one way, as we generally shall, they are of the form if a occurred, then even if any events or conditions logically consistent with a and b had also occurred, in place of those which did, b would still have occurred. Or, as we can as well say, Even if any events or conditions logically consistent with a and b had occurred, rather than those which did, if a occurred then b did. Or again, independent nomic conditionals come to this: Given the rest of the world as it was, or given that it was different in any way we can conceive it as being, without logically excluding a and b, then if a happened so did b.
Independent conditional statements are thus different in kind from those dependent nomic conditional statements or simply dependent conditionals, which state the first four of our causal relations. Dependent nomic conditionals are certain of the statements of the form If a occurred, then b occurred. Their truth, in brief, is dependent on what else is true.
By way of abbreviation of what is stated by the independent conditionals in (5), cc can be said to have necessitated e, and e can be said to have been necessary to cc. We can also, in abbreviation, speak of an event as necessitated without identifying or indeed knowing its causal circumstance. Here a necessitated event is of course to be understood as an event which does stand in the given relation to some or other antecedent. Like remarks might have been made elsewhere— with respect to a required event, for example. What we have in (5) might be improved in a number of ways so as to deal with questions and indeed objections, and thereby complicated and indeed greatly complicated. In particular the contrapositive formulation might be considered further. What we have, further, might be expressed in several different logical notations. We might consider problems (e.g. Wiggins, 1973) and proposed solutions (e.g. Thorp, 1980, pp. 16-26) which arise in connection with notations. What we have will suffice as it stands. It does indeed distinguish yesterday and last night from the other instance of constant conjunction, the solar conditions and last night. The solar conditions but not yesterday count as causal ^ circumstance for last night. There is no peculiarity, incidentally, about this particular very grand causal circumstance and effect. Reflection on smaller examples of causal circumstance and effect, such as those with which we began, is quite as capable of illustrating this fifth causal connection.
The given connection between causal circumstance and effect is in fact the principal instance of what can be called fundamental nomic connection or fundamental necessary connection. Such connection is what is stated by independent nomic conditionals and, of course, holds between any two things when it is true that if or since the first occurred, then even if any change logically consistent with either had also occurred, the second would still have occurred. Fundamental nomic connection, as will be made clearer, is just that—fundamental. It is the stuff of or the basis of all the relations specified so far or still to be specified between cause and effect, causal circumstance and effect, and nomic correlates.
There are two more causal connections to be noted. As we saw earlier, (2) an ordinary causal circumstance is required for its effect. If, say, the ten conditions including the flipping of the switch had not occurred or existed, the wipers would not have started. This is a truth dependent on the situation as it was—there was no ad hoc electrical -circuit and so on. There are related connections, however, which have the independence of (5) the connection just noted. One is bound up with the fact that we do indeed suppose that there is some set of types of circumstances, each type related in the same way to startings-to-work of the wipers. We believe that if the wipers did start, even if certain changes had taken place in the situation, there would have occurred an instance of one or another member of this set of types of circumstances. Either the switch was flipped and other conditions existed, or an ad hoc electrical circuit was completed and other conditions existed, or. ... More generally, suppose again that cc was a causal circumstance for e. Suppose also that any one of cc' or cc" or. . ., if it existed, would also have been a causal circumstance for e, and, we might add, would not have been part of a causal sequence including cc. Then
(6) If none of cc or cc' or cc" or ... existed, even if there occurred any change x consistent with that and with e's absence, e would still not have happened. If e happened, at least one of cc or cc' or cc" or ... existed, even if there also occurred any change x consistent with both.
By way of abbreviation, one or another of a set of possible circumstances was necessary to e, and e necessitated the occurrence of one or another of the set.
Our last relation follows on from this. In terms of the example it has to do with the fact that if in the situation there existed only the one circumstance for the starting of the wipers, then, even if certain other events or conditions had occurred or existed, the wipers would not have started. More generally, if cc was a causal circumstance for e, and ! with the other terms defined as with (5), we have this:
(7) If none of cc' or cc" or. . . existed, then if cc had not existed, even if any change x had occurred logically consistent with that and with e's absence, e would not have happened. If none of cc' or cc" or. . . existed, then if e happened, cc would still have existed even if any change x had occurred consistent with e and cc.
By way of abbreviation, for what it is worth, we can say that cc was dependency necessary to e, that e was such as to dependently necessitate cc.
Our principal conclusion about causation is now at least in distant view. Causation and other nomicity consists in no less than, and not greatly more than, a web of connections between things or events, at bottom individual properties. What are these connections? They are those asserted by the two kinds of conditional statements. Causation is not, as some suppose, anything less than these connections—which conclusion will be defended in what follows. Nor is it greatly more. There is thus a clear and plain answer, if one which requires complication, to the question of what causation and other nomicity comes to.
The web may be open to other styles of description. Any of these must give it as having a certain structure. Each of the connections stated by independent nomic conditionals gives rise to others. For example, suppose cc necessitated e, e thus being necessary to cc, and that cc consisted in c and c'. It follows that if e had not occurred, and c' had occurred, then c did not occur. We shall not pursue these matters i further here, but they will be noticed again in connection with the nature of conditional statements and the subject of causation and science. (1.4, 1.6)
It is worth emphasizing what has already been said or implied, that all seven of the connections at which we have looked, and the further subordinate ones at which we shall not look, are indeed objective connections, connections in reality. They are entirely independent of minds, theory, conceptual schemes, the statements which state them, and so on. There are philosophers, some of them inclined to Kant's doctrine that we impose the category of causation on reality, some of them freer spirits, who think or at any rate say differently of causation „ and of nomic connection generally—in a phrase, that it is part of the mental order. One of these philosophers presses on forward, with agreeable audacity, to characterize the view I have expounded as Idealist or even Scholastic. (Putnam, 1983) That is, the view expoun-ded is seen as one which 'mentalizes' the natural world by intruding the mental order—nomic or necessary connection—into it. The view, on the contrary, is precisely one of Causal Realism rather than Causal Idealism. (Kim, 1981) It is exactly unlike any theory which does somehow locate nomic connection in the mental order, whether or not it then relocates it elsewhere, and thus is properly labelled Idealist.
The point stands in connection with another. Those familiar with philosophical writing on causation, or touching on causation, will have noticed that our analysis so far of it has taken the terms 'necessary connection', 'nomic connection', and 'lawlike connection' as synonymous, but has made little reference to laws. The analysis may appear to be unlike those which, to speak quickly and only of one central matter, describe something like a causal circumstance and an effect as two items which fall under a law, and then proceed to attempt to give an account of what a law is—a true proposition of a certain character. (Hempel and Oppenheim, 1953; Hempel, 1965) These different analyses may appear to describe a connection in reality by -way of what can be called our linguistic response to it, or the character of our belief about it. In fact, our analysis and these seemingly different analyses are basically alike. Both characterize connections in reality and both give an account of the character of our beliefs about them. It could not be otherwise.
Our analysis, in a way more direct, specifies necessary connections, but in so doing does provide an account of the nature of laws. It does so by actually giving their form or structure. The most fundamental kind of them are independent nomic conditional statements, general rather than particular. Laws of the fundamental kind thus are general propositions to the effect that if something is the case, then no matter an alteration in certain logically consistent concomitants, something else is also the case.
The alternative procedure, although its focus is different, is indeed basically alike, as it must be. Here, one starts with a connection in the world, and appears to describe it by way of our characterization of it, the character of our belief about it. To do the latter thing, however, if the procedure can have any hope of success, is to describe the connection in the world. If it were not to do this, it would be no more than the futility of changing or avoiding the subject.
1.4 THE ANALYSIS OF CONDITIONAL STATEMENTS
What we mainly have in answer so far, about causes and causal circumstances, is that they stand in seven connections—the last three of which are also fundamental to what will be said of nomic correlates. All are connections stated by either dependent nomic conditionals or independent nomic conditionals. What we need now, to have a better grasp of these connections, is a better grasp of the two kinds of statements. To understand them more fully is to see more clearly what we believe about the real connections, connections in extra-linguistic reality. The subject of dependent nomic conditionals has for long been a disputed one, and part of larger disputed subjects, those of larger categories of 'if' statements and of 'if' statements generally.
Dependent conditionals can initially be identified, as they have been >. here, as typified by the 'if statements we accept in connection with our standard causal beliefs—'If the switch hadn't been flipped, the wipers wouldn't have started', 'Since the switch was flipped, the wipers started', and the like. The idea, of course is not to elucidate dependent conditionals by relating them to causal statements and the like, but to do just the opposite. It will be convenient, by the way, to abbreviate the conditional 'If the switch was flipped, the wipers started' not merely to 'If / occurred, then s occurred', as we have already, but to 'If F then S'. So too with all other conditionals: letters in lower case for events, conditions, and the like, the same letters in upper case for the statements that the event occurred or the condition existed. The custom will in fact be followed generally hereafter, with subjects other than that of conditionals.
Dependent nomic conditionals are readily distinguished from a number of other sorts of 'if statements. First, they are not logically or conceptually necessary, as is 'If she has children, she is somebody's mother.' That they are not such statements is in accord with the fact, rightly insisted upon by Hume, as already noted, that causes cannot be said to be in a certain logical connection with their effects: the fact that it is not contradictory, however mistaken it may be, to assert that a causal circumstance for an event existed but that the event did not occur.
Dependent conditionals, secondly, are not to be identified with the 'material conditionals' of truth-functional logic, which rarely if ever turn up in ordinary language. The 'material conditional' is customarily written as P ] Q. It is only misleadingly expressed as If P then Q, as is now widely accepted. (Bradley and Swartz, l983, pp. 226-9; Anderson and Belnap, 1962) The material conditional P ] Q is true solely in virtue of P and Q both being true, or both false, or P being false and Q being true. It is not true in virtue of any further relation between P and Q. It is false only when P is true and Q false, and false solely in virtue of those truth-values of its parts. Despite ingenious if strenuous attempts (Grice, 1975; Ayer, 1972) to present 'if statements in general as being material conditionals at bottom, it is evident enough that our If F then S is not true solely in virtue of the antecedent and consequent being both true or both false, or false and true respectively. (Mackie, 1973a)
Thirdly, dependent conditionals are unlike a very considerable and mixed assortment of 'if statements, (i) 'If she feels so strongly, she'll decide against it.' (ii) 'If he is reasonable and understands the facts, he'll send the letter.' (iii) 'If you want them, there are biscuits on the sideboard.' (iv) 'I could have if I chose to.' (v) 'If I'm awake the sun will rise and if I'm not awake the sun will rise.' (vi) 'Since you moved your arm that way, you waved.' (vii) 'The offer was made and accepted, so there's a contract.' (viii) 'If that was painted in the eighteenth century, I'm a Dutchman.' (ix) 'If you were Julius Caesar, you wouldn't be alive.' These are in various ways different, as reflection will show, and raise different questions. What is common to all of them and to others, as it is to the first two sorts of 'if statements, is that none states the kind of connection of one thing with another which is expressed by any dependent conditional.
This general distinction, clear enough despite our not having an analytic account of it, is in part brought into sharper focus in a somewhat unexpected way. There is a difference, although an uncertain one, between some statements of the form If P then Q and others of the form If P, Q. (W. A. Davis, 1983a) Suppose that someone has unkindly disconnected the wiring between the switch and the wipers. It makes sense to say, and in a certain situation it will be true, that (1) if the switch is not flipped, the wipers will not start. One can say quite as truly in this way, of course, that (2) if the switch is flipped, the wipers will not start. (The case is then like (v) above.) But is it true that (3) if the switch is not flipped, then the wipers will not start? On the contrary, it seems false. This is so since this third statement asserts the existence of a connection between two things (no flipping and no starting), and ex hypothesi no such connection exists. The first statement, like the second, can naturally be taken as not asserting such a connection, and hence can be true. The third statement is a dependent nomic conditional, while the first, whatever else is to be said of it, is not. The point is instructive, but it would certainly be mistaken to suppose that all ordinary conditionals are of the form If P then Q and all other 'if statements of the form If P, Q.
Dependent nomic conditionals can also be characterized in terms of their logical properties in a narrow sense. Let us notice two of these. The seven connections surveyed above (1.2, 1.3) were stated by both a conditional and its contrapositive. Dependent nomic conditionals, as can be anticipated, in fact have the logical feature that they do simply entail their contrapositives. If not-F then not-S entails If S then F, and the latter entails the former. If F then S entails If not-S then not-F, and here too the latter entails the former. That there is this mutual entailment with respect to the two members of each pair is, or is intimately connected with, the proposition that the two conditionals state the same fact of connection between two things in the world. The feature of entailing their contrapositives distinguishes dependent nomic conditionals from certain other 'if statements. Some of these are exemplified by (iii) and (iv) above. From 'If you want them, there are biscuits' it does not follow that if there are none, you don't want any, and from 'I could have if I chose to' it does not follow that if I didn't choose to do the thing, I wasn't able to do it.
Dependent nomic conditionals also have the logical feature that they are transitive. That is, IfP then Q and If Q then R, where these are such conditionals, entail // P then R. It has sometimes been said that certain other 'if statements are not transitive—for example, 'If J. Edgar Hoover had been born a Russian, he would have been a Communist', 'If , he had been a Communist, he would have been a traitor', and 'If he had been born a Russian, he would have been a traitor'. (Lewis, 1973, p. 33; Stalnaker, 1975, p. 173) It is said that this proves the failure of transitivity—the three statements are unexceptionable and the third does not follow from the first two. There is the objection, however, whatever else is to be said, that the third statement fails to follow from the first two only because of an ambiguity—and more precisely because the consequent of the first conditional is in fact not identical with the antecedent of the second. We do not actually have in this supposed counter-example to transitivity what we must have, state-ments of the forms If P then Q, If Q then R, and If P then R. (Mackie, 1980) Certainly, whatever is to be said of transitivity elsewhere, dependent nomic conditionals are transitive. They are thus perfectly suited to the analysis of our beliefs about causal chains or sequences. Certainly from the facts that r caused s, and s caused t, it follows that r caused t.
Are dependent conditionals to be characterized more generally in terms of two categories to which philosophers have given much attention, those of subjunctive and counterfactual statements? This seems often to have been assumed. To have a new example, consider the statement that (A) since it is raining, the balcony is wet. It is an indicative conditional, a conditional in the indicative mood. Consider also the statement that (B) if it were raining, the balcony would be wet. It is subjunctive. Is only one of these, perhaps the second, a dependent conditional in the sense we have in mind? No, both statements, although they are different in mood, are such conditionals. (A) is part of what is stated by stating that rain is making the balcony wet, or causing the balcony to be wet. (B) is part of what is stated by stating that rain would make the balcony wet. The distinction between our dependent conditionals and others is thus not a difference between the indicative and the subjunctive mood.
It is as clear that another difference between (A) and [B] is no more relevant. (B) is counterf actual: it implies the falsehood of its ante-cedent. (A), called by some a factual conditional, implies that its antecedent is true. The difference is not the distinction between the class of dependent nomic conditionals and other 'if statements. Both (A) and (B), to repeat, are dependent conditionals. So is what is sometimes called an open conditional: If it is raining, the balcony is wet. It carries no implication as to the truth or falsehood of its antecedent.
Dependent conditionals have often not been distinguished by philosophers from one or another larger category of 'if statements. Partly because of this fact, dependent conditionals have been taken as problematic. The principal problem about them has generally been said to be that of their meaning or semantics. The problem is to define , the meaning of conditionals, to say what it means to say that if kangaroos had no tails they would topple over, to say exactly what conditionals mean. (Goodman, 1965, p. 17, p. 23, cf. p. 14; Ayer, 1972, pp. 120 f., cf. p 118; Lewis, 1973, p. 1; Mackie, 1973, p. 64) As a look at the philosophy of language and its analyses of 'meaning' or its uses of 'semantics' quickly shows, much more would need to be done to give us a well-defined problem, but let us not linger. The vague expression of it is sufficient for our purposes. Let us rather glance at two of what are presented as solutions to the problem, the metalinguistic and the possible-worlds proposals. By doing so we shall become clearer about the problems of nomic conditionals, and hence their solutions. We shall also avoid a doubt about what will be maintained here.
The metalinguistic proposal (Goodman, 1965), so named because, at any rate in the first instance, it presents conditionals as being about other linguistic entities, is along the following lines. What is it to say that if (R) it is raining, then (W) the balcony is wet? Roughly, it is to say that the statement (R), and (C) true statements of certain conditions, and (L) a true lawlike statement, together entail the statement (W). The proposal, as is allowed by its proposer, faces serious problems, notably that of explaining the nature of a lawlike statement. It is nonetheless advanced as being on the right lines.
The possible-worlds proposal can most easily be stated briefly in terms of a dependent conditional that is counterfactual. To say that if it were raining the balcony would be wet is to say this: among possible worlds where it is raining, the one which overall is most like our actual world is also one in which the balcony is wet. (Lewis, 1973; cf. Stalnaker, 1975) Or, to interpret the idea in a way less ontologically extravagant, a way which does not seem to commit us to a plurality of somehow existing worlds, what the conditional means is this: if our actual world were different in that it were raining, and differences overall were in a sense the smallest possible, the balcony would be wet. One source of this theory, to continue in terms of the example, is the truth that if it were raining, more other things would be different than that the balcony was wet. For a start, there would be a cause of the rain, and further effects of it—a wet garden and so on. This prevents us from supposing that the conditional in question, to speak in the ontologically extravagant way, comes to this: in the possible world where it is raining, but everything else is the same as in this world save that the balcony is wet, the balcony is indeed wet.
What we must then do, it is supposed, is to turn our attention to a primitive idea of over-all similarity between possible worlds. This has to do both with what are called states of affairs, which we may take ultimately to be a matter of individual properties, and also what are called laws. To note a possibility to which we shall return in a moment, it is allowed that a possible world w' might be more like our actual world than a possible world w" even though the laws of our world are to some extent suspended or do not exist in w' and are intact inw".
A bit more will be said of particular features of the metalinguistic and possible-worlds proposals, but let us first consider something common to both of them and indeed to other proposals. All of these, to repeat, although there is some uncertainty and inconsistency, are presented as answers to the question of the meaning or semantics of certain 'if statements, certainly including dependent nomic con-ditionals. To think about this even for a moment is to see that something is amiss.
Does 'If it's raining the balcony is wet' mean, in however large a tolerable sense, something about other conditions—say the absence of a canopy over the balcony and so on? As was maintained earlier (1.2), surely not. The unsatisfactory conclusion that the conditional is about so much, or rather the unsatisfactory conclusion that the conditional is about a further statement about so much, follows from the metalinguistic view. At any rate there follows some such unsatisfac-tory conclusion pertaining to other conditions somehow described. Again, does 'If it were raining the balcony would be wet' mean something about other ways that the world would be different, over and above the balcony's being wet, if there were the difference that it was raining? Is the given conditional in part about a cause of rain, or the wet lawn? It is a remarkable idea, not made better by bravely labelling the conditional enthymematic. The unsatisfactory con-clusion, or a related one, follows from the possible-worlds view.
The views are more plausible when taken as answers, or at any rate materials for answers, to a question quite different from the question of meaning. They are more plausible when taken as responses to a question about dependent conditionals which in fact has more claim to be regarded as the principal one. It can be called the logical problem, and briefly expressed it is this: in general, what are the premisses or grounds or bases for dependent conditionals? It is not the question of what in general we say when we assert such conditionals, or what they are about, but the question of what reasons we have for saying what we do. (This is the question that is fundamental with every sort of 'if statement.) It is our reasons for asserting a dependent conditional which bring in a good deal more than what is brought in by the conditional itself. That there was no canopy may be part of why I say that if it's raining the balcony is wet, but it is not part of what I say.
The metalinguistic view remains in several ways odd and indeed unsuccessful when regarded in the more plausible way. It may be said to be on the right lines, but at best it provides materials for an answer to the logical question, materials which it does not combine properly. Further, so to speak, one of the materials is indeed inadequate. If we are seeking an explanation of the grounds of dependent conditionals, and one of these is given as a lawlike statement, we do indeed require an explanation of the nature of such a statement. As for the possible-worlds view, of which a great deal might be said, it too seems to involve an unanalysed notion of law, although the matter is more obscure here.
Let us notice only a clear objection for which the way has been prepared. What we have as premiss for the dependent conditional that if it were raining the balcony would be wet is roughly this: in that possible world most like our own in which it is raining, the balcony is wet. But it is specifically allowed that that world might lack our laws, including a law which pertains to the rain and the wet balcony. In that world, to be brief, it could be an accident or mere coincidence that the rain was accompanied by the balcony's being wet. That could not be our reason for asserting the given conditional, whatever else is. (Cf. L. J. Cohen, 1980; Pollock, 1976; Swain, 1978.) Whatever the strengths and interests of possible-worlds conceptions in several inquiries, notably formal semantics, we do not here have an acceptable answer to our question.
On what basis can we assert the dependent nomic conditional that if (R) it is raining, then (W) the balcony is wet? The short answer is that we assert it on the basis of two things, an independent nomic conditional, and (C) a belief about certain conditions, which is a belief that the antecedent of the independent conditional is in a certain part true. Again, we assert it since we accept (i) an independent nomic conditional roughly to the effect that in the world as it is, and within certain large limits as it might be, if it is raining and certain other things are the case, then the balcony is wet, and we also accept (ii) that those other things are the case. It follows that if it is raining then the balcony is wet.
To be more explicit, it is simplest to take the particular formulation of the independent conditional just suggested, and anticipated earlier (1.3), in place of If R and C, even given any X consistent with R and C and W, then still W. That is, let us have this: Given the world as it is, or given any changes in it logically consistent with R and C and W, then if R and C then W. From these two things it follows—as from If A, then if B then C, and A, it follows that If B then C—that If R and C, then W. From this in turn, together with C, there follows the dependent conditional If R then W. To repeat, let us have the statement (Y) describing the actual events and conditions accompanying r and c in the world as it is, and the disjunctive statement (X) to the effect that the world is in one way or another otherwise, logically consistent with R and C, and W. Then our premisses and conclusion are as follows.
If Y or X, then if R and C then W.
Y.
If R and C then W.
C.
If R then W.
This answer to the logical question about dependent nomic conditionals is reassuringly persuasive. Certainly it involves no unexplained notion of a lawlike statement. That is not to say that it involves no notion of a lawlike statement, or, to speak of reality rather than our language for it, no notion of lawlike connection. It is unthinkable that any arguable account of dependent conditionals could be without a notion of lawlike connection, and hence of law or lawlike statement. As can properly be said, the answer just given to the logical question rests essentially on an explained notion of lawlike connection. 'Lawlike connection' is simply another term for what was earlier (1.3) called fundamental nomic connection or fundamental necessary connection—and for connections related to it. Fundamental nomic connection is the connection stated by independent nomic conditional statements. To rest an answer to the logical question about dependent nomic conditionals on independent nomic conditionals is to answer the question in terms of explained or analysed lawlike connection. The plain answer also has other virtues (Honderich, 1982a), but they need not be sung here.
As for the meaning of dependent conditionals, it is possible and perhaps necessary to say of them, as it is commonly said of 'if statements of various kinds, that they are to be taken as primitive, in the sense of not being open to analytical definition or reductive analysis. (Certainly one only gets something synonymous, at best, and no analysis, by rendering 'If P then Q' as 'On the assumption that P is true, so is Q' or 'In a possible world where P is true, so is Q'.) Dependent conditionals are thus to be regarded in the way of the primitive conception or conceptions at the base of any logical system. That is not to say, however, that their meaning cannot be character-ized. It has been here, in what has been said already. Their meaning is such that they are to be distinguished from various other 'if statements, that they have certain logical properties, and that they are entailed by independent nomic conditionals together with further premisses in a way derived from the antecedents of the latter conditionals.
To turn now to independent nomic conditionals, they can be identified initially, as they have been, as typified by 'if statements we accept in connection with our beliefs as to causal circumstances and effects. They can, as we know, take the form illustrated by this 'if statement of our current example: If R and C, even if X, then still W. Their meaning is evidently quite other than that of dependent conditionals, since they are in part and in a way general. Each such conditional asserts, with respect to all events or conditions of a certain class, that the occurrence of any or any set of them, or indeed all of them, would none the less leave it true that if the conditional's antecedent is true, so too is its consequent. By antecedent, in terms of the example, I of course mean only R and C. In virtue of this fact of generality with respect to independent conditionals they are not tied to a particular situation, as are dependent conditionals. Their truth is not dependent on a particular situation. They can be expressed formally in several ways, making use of the resources and notations of different logical systems, but are perspicuously expressed in just the forms we have. We can, as with dependent conditionals, distinguish them from other 'if statements, specify their logical properties—including con-traposition and transitivity—and give their logical relations, notably their relations to dependent conditionals.
On what is such an independent conditional as If R and C, even if X, still W based? The answer, in brief, is the method of empirical inquiry, at its best the method of science. There can be no doubt whatever about the validity of this method, and no doubt either that its description has been and remains a matter of controversy, or of several controversies. One of these, perhaps the most general and fundamen-tal, has to do with the problem of induction. What is the explanation of the rational justification we evidently have when we reason in certain ways from certain premisses to particular or general conclusions about the world? What is the explanation of why I am right to conclude, as I am, that if it is raining and certain other things are true, the balcony is wet—and, in brief, that it would be wet no matter what else were true? The explanation will include, certainly, past situations both like and unlike the present one—like, in that they included events and conditions of the same type as r and c; unlike, in that they included events and conditions of other types than those accompanying r and c. The explanation will also include what is related to this and is absolutely fundamental to scientific method, which is the experimen-tal procedure of testing and establishing connections by the 'varying of circumstances', which is essentially the discovery of what is relevant and what is irrelevant to a given event. (Mill, 1961 (1843), p. 249; Keynes, 1952, p. 393; Carnap, 1962, p. 230; Honderich, 1991 ?)
To say this much of the method of empirical inquiry, above all the method of science, is of course to say little more than nothing. Anything like an adequate account of the method of empirical inquiry is out of the question here. One separate point is clear enough, however. It hardly needs remarking that the experimental procedure of varying the circumstances fits exactly the account of fundamental nomic connection which we have. It fits that account better than it fits others, including a probabilistic account of which a bit more will be said. (Skyrms, 1980, p. 16) That is a further if subsidiary argument for the account.
One thing remains to be noticed. It is now clearer than before (1.3) how fundamental nomic connection, the connection stated by inde-pendent conditionals, is either the stuff or the basis of all the seven causal connections. It is the stuff, so to speak, of the last three—(5), (6), and (7). It is the basis of the first four—(l, la), (2, 2a), (3), and (4). It is the basis in the sense that each of the dependent conditionals rests on some independent conditional and a further premiss related to the antecedent of the independent conditional. Consider the dependent conditional (3) If c occurred, so did e. Consider also If cc occurred then, even if there also occurred any change x logically consistent with cc and e, it was also the case that e occurred—which is the first part of the independent conditional in (5). Circumstance cc, we take it, consisted in c and also in c', c", ... As with the example lately considered, it is evident that (3) is entailed by the given part of (5) together with a statement of the occurrence of c' c", ...
It would be rash to make the conclusions of this chapter depend absolutely on exactly the account of certain 'if statements that has now been given or intimated. These statements, as already remarked, make up a controverted subject. (Sanford, 1988) It is complete with competing predilections, schools, logics, methods, and termino-logies—and indeed competing conceptions of the subject, by which I mean conceptions of just what 'if statements are properly treated together. What I hope to have shown, which is consistent with a certain tentativeness about what has been said, and with incomplete-ness, is that we do have a grasp of both dependent and independent conditionals, which grasp can be clarified and which gives to us an explicit understanding of the seven causal connections that were set out. It is not as if conditionals of the two sorts were near to being sufficiently problematic or obscure as to make it unprofitable to use them in elucidation of causes and effects, causal circumstances and effects, and—to look forward—nomic correlates.
1.5 CAUSAL VERSUS OTHER NOMIC CONNECTIONS
We take causal circumstances and causes to have a nature lacked by effects. This nature presumably explains the truth that if a is a causal circumstance or cause of b, then b cannot be such of a. We ordinarily say of causal circumstances and causes that they make their effects happen, but we do not say, and will deny, that effects make either of the two causal items happen. The philosophical variations on this usage are many. The causal items are said to be active, to be productive, to be geneses, to have potency or efficacy. Some philos-ophical writings on causation consist in good part in a somewhat numinous insistence on the distinctive nature of the causal items as against their effects—causes, for example, are declared to be 'powerful particulars' or 'forceful objects at work'. (Harre and Madden, 1975)
We also say of causal circumstances and causes that they explain their effects, in a sense in which effects do not explain the causal items. Here, there is less possibility of philosophical variation, but this second characterization of the nature of the causal items is perhaps as important as the first. Finally, we take it that effects depend on the causal items, and that the latter do not in this way depend on the former. It is perhaps a good deal less than certain that this third characterization is conceptually distinct from the first two. I shall suppose it comes to much the same.
In our inquiry into causation so far, we have not attended specifically to this fact of difference or asymmetry between causal items and their effects—the fact of causal priority as it is sometimes called. We do indeed have it that a causal circumstance necessitated its effect. But to assert that is by definition to assert no more than a certain independent conditional—roughly, that since the circum-stance existed, even if most other things had been different, the effect would still have occurred. We also have it that effects do no more than dependently necessitate their causal circumstances. That is to say, roughly, that if the effect occurred, and no other causal circumstance for it but one existed, that one would still have existed even if most other things had been different. It is not obvious, although it may be true, that the ideas that a causal circumstance made its effect happen, and explained it, and that the effect depended on the circumstance, somehow come to no more than these independent conditional claims. Philosophers have sometimes denied that the asymmetry between causal items and their effects is a matter of connections stated by 'if statements. These, they feel, are not enough.
Certainly we cannot rest with the three ordinary ideas we have of the distinction between the causal items and their effects. The first idea is of a metaphorical and anthropomorphic kind, and the second and third also call out for analysis, if only for the reason that there are other non-causal pairs of things such that the first explains the second and the second depends on the first. The obvious example is that of the premiss and conclusion of a deductive argument. It is not that kind of explanation and dependence that is in question with causation. What kind it is needs to be explained.
If we cannot rest with the ordinary ideas, we can no more rest with their philosophical variants. It is all very well to insist that causes have or are powers or whatever, but we need to know what is to be understood by that. They do not give commands and they are not premisses from which many or important conclusions follow. Nor does it seem likely that the idea of causal power is not open to analysis, or, what comes to much the same, that it is somehow to be acquired without noticeable effort by thinking on what is common to such verbs as 'push' and 'pull', as has sometimes been supposed.
One persistent analytical account of causal priority does seize upon an indubitable truth, that causal items stand to their effects as our means to our ends, while no effect is our means to its cause or causal circumstance. When it is true that an effect—the wine bottle's being open—is my means, it is not such as an effect but as a cause of something else, which other thing is not a means to it. We do indeed manipulate and control our surroundings, in so far as we can, by way of things as causal rather than as effects. However, there is the immediate objection that not all causal items are the means of someone. No earthquake is, and in fact relatively few causal items in the natural world are such. The attempt has been made, inevitably, to extend the idea of a means to cover all causal items, (von Wright, 1971; Mellor, 1986) This stratagem is not reassuring, for several reasons, but there is a more fundamental objection which applies even to those causal items which really are our means.
It is that the fact that a causal item is a means is not a fact about it, but a fact about us. The fact that a cause of the wine's being cool, say refrigeration, is my means—this is the fact that (i) I can bring about that cause, and (ii) it is a cause of what I desire. This thought, that the given cause of the wine's being cool is not in or of itself a means, is reinforced by the truth, among others, that the given cause is precisely not a means to my idiosyncratic drinking companion, who likes his Haut Poitou uncooled. But the asymmetry of causal items and their effects is, of their very nature, a fact about them, a fact which would persist in a world devoid of desires, and, as might be added, a world devoid of our capability of bringing things about.
Is it possible to explain the asymmetry by way of a clear idea of power—or capacity, ability, or disposition? Well, we can give a certain clear sense to saying that the hot coffee is able or has a power to dissolve the cube of sugar. What it is in general for a thing a to have the power to produce b is for it to be true that an individual property or properties of a, together with other things, will constitute a causal circumstance for b. Anything that is a cause, then, is in this clear sense a power, a power to produce an effect. (Cf. Ayers, 1968.) There is a related secondary sense of the term 'power' and like terms, where the power is the class of differing individual properties or property-sets, each of which is nevertheless alike in entering into some causal circumstance for one effect. Or, better, a power of this kind is the class of types of such properties or property-sets. In this sense, hot coffee can be said to share a power to dissolve sugar with steam, certain chemicals, and so on. The secondary sense is clearly dependent on the primary.
We need to reflect, however, on what has just been said: in brief, that for something to be or to have a power in the primary sense is for it to enter into a possible causal circumstance. Given our account of causal circumstances, that is fundamentally to say, in line with the independent conditional (5) set out in Section 1.3 and mentioned at the beginning of this section, that for a to have the power to produce b is for roughly this to be true: If A & C, even if X, still B—where C asserts the existence of other conditions or events. The difficulty is that a like conditional (derived from the independent conditional (6) also set out in 1.3) may well be true of b. That is, it will be true, if there is no other causal circumstance for b on hand, and no alternative for a, that If B & C, even if X, still A. To speak informally, in terms of the example, the hot coffee together with other things guaranteed dissolved sugar, but it may also be true that the dissolved sugar, together with (different) other things, guaranteed the hot coffee. The upshot of this is that in this sense of 'power'—as of many like terms—it is at least arguable not only that a cause has a power to produce its effect, but also that an effect has a power to produce its cause. Here we have no adequate difference between cause and effect. It is true, somehow, that a cause has a power in a sense that an effect does not, but we have not got that sense.
There is the further grave difficulty about the idea in hand, as a little reflection will show, that in the given sense no causal circumstance, as distinct from cause, has the given power. Leaving aside several other good attempts to explain the difference between causes and causal circumstances and their effects, and also what can be said of great obstacles in the way of these attempts (Mackie, 1974, Ch. 7, 1979; Ayer, 1984a; Sanford, 1976, 1985; Papineau, 1985b; Honderich, 1986), let us return to and concentrate on our ordinary convictions about the difference.
What do we have in mind in taking it that a causal circumstance makes an effect happen? A good answer is that we regard the causal circumstance as leaving no room for any other eventuality than the effect. The causal circumstance settles that but one of certain possibilities becomes actual. Most plainly, the causal circumstance fixes or secures the occurrence of just one thing, as distinct from fixing the occurrence of that thing or a second or a third or. ... What do we have in mind in taking a causal circumstance to explain an effect in the given sense? There are the same good answers. It is for the circumstance to leave room but for one eventuality, for it to settle things. It is not for the circumstance to give rise to something or other, but for it to give rise to just the effect.
These several glosses of the characterization of a causal circum-stance as making its effect happen and explaining it, glosses which are surely very natural, lead us to a firm conclusion, one that may be anticipated. If it is not obvious, as remarked before, it surely is true that the nature of causal circumstances and causes, as against effects, is, at least in good part, explained by what we have already—it is explained in good part by the fact that causal circumstances necessitate effects, and effects merely necessitate one causal circumstance or another. That is, to simplify the independent conditional (5) a bit, a causal circumstance is such that if it happens, then just its effect does. But, to simplify (6), an effect is such that if it happens, then all that is true is that one or another of a set of causal circumstances has existed.
The clear distinction made by these two conditionals gives a clear sense to talk, mainly by philosophers, of causal circumstances having a power lacked by effects, and so on. To revert to what is fundamental, the distinction made by the two conditionals gives some clear sense to our saying that causal circumstances explain effects, and make them happen, and not the other way on. More needs to be said about our conviction, but here we have something. We have in a causal circumstance by itself a complete answer to the question of why an effect occurred. We do not have, in just an effect, such an answer to the question of why a causal circumstance occurred. That we do not have such an answer, it can be argued, is the fact that what follows, from the occurrence of the effect, is only that that circumstance or another occurred.
I have latterly been speaking only of causal circumstances, and not causes. What has been said can be extended to them. That is, in brief, it is reasonable to suppose that their nature, as distinct from that of effects, is to be explained by their membership of causal circum-stances. What has been said, however, seems not enough. It is, I think, one of two parts of an adequate account of causal asymmetry. The additional part, which does not have to do with the connections stated by independent conditionals, is perhaps particularly necessary in connection with our conviction about the explanatoriness of the causal items.
Both that conviction, and the conviction that the causal items make their effects happen, can also be glossed as convictions that the causal items bring into existence their effects. Given this, it is impossible to avoid the idea that another part of the difference between the causal items and their effects is that the causal items exist at a time when their effects do not. They exist before their effects. If all causal circumstances and causes precede their effects in time, it seems we have in that temporal consideration a second basis for the asymmetry we are considering. Do all of what we take to be causal circumstances and causes precede their effects? Here there is a large philosophical dispute, and we shall be told by some that the answer is no. Is there not a causal circumstance, including the weight of the driver, for that simultaneous effect which is the flattening of the seat cushion?
One thing that can be said in opposition to the simultaneity idea is that if we persist in thinking precisely of causation, of one thing causing another, as distinct from any related kind of connection, we are inclined to try to substitute successions for simultaneities. We are inclined to think of connections between earlier and later events rather than connections between simultaneous events. The flattening of the seat cushion at this instant is owed to the driver's weight at a prior instant. The last instant of the flattening of the cushion, we are inclined to think, will be simultaneous with the beginning of a causal circumstance for the cushion's being other than flattened. In this inclination to take the causal items as prior to their effects, incident-ally, we have the support of a good deal of science, indeed a strong scientific tradition, having to do with the principle of retarded action. (Bunge, 1959, p. 62f.)
In our ordinary thinking about causation and time there evidently is uncertainty, as is not the case elsewhere. In some respects there seems not much room for argument about our conception of standard effects and their causal circumstances. There is surely no doubt that we take them to involve the necessity relations and the relations of required-ness. In connection with time, our conception is not settled. This fact is consonant, to say the least, with the long philosophical dispute about causation and time, including the idea that causes might not only be simultaneous with their effects but might come after their effects. (Dummett, 1954) If we are subject to uncertainty, there is room for decision, as distinct from discovery. The definition we shall adopt here, in the tradition of Hume and many others, is one that takes causal circumstances and hence causes to precede their effects in time. It allows us the conclusion that has just been contemplated: that the difference between causal items and their effects has its basis not only in the consideration that causal circumstances fix uniquely the occurrence of their effects, but also in the consideration that causal circumstances precede their effects. The definition is adopted, of course, not merely for the reason that it gives us a further explanation of the difference between causal items and their effects. It has an independent recommendation, although one that needs more argu-ment that has been supplied here.
Given the account we have of the difference, we can now proceed quickly to a final characterization of a causal circumstance. We have everything in hand save one consideration, having to do with non-redundancy. The difference between causal circumstances and their effects, further, is what distinguishes causal circumstances and effects from other things also in nomic connection, which is to say nomic correlates. We can also proceed quickly to a characterization of these.
We began with the idea that a causal circumstance consists in a set of conditions including a cause or causes—more precisely a set of individual properties—each being (1, la) required or alternatively required for the effect. From this it followed (2, 2a) that the circumstance too is required or alternatively required for the effect. Further (3) each condition requires the occurrence of the effect, and so too (4) does the circumstance as a whole. As for the fundamental necessity-relations, (5) the causal circumstance necessitates the effect, and hence the effect is necessary to the circumstance. (6) Also, the circumstance is one of a set of circumstances necessary to the effect. Further (7) the causal circumstance is dependently necessary to the effect, which is to say that the effect dependently necessitates the circumstance. We have it too (8) that the circumstance (whose constituents need not be simultaneous) is prior in time to the effect. It is in virtue of (5), (7), and (8) that we can truly say that the circumstance makes happen and explains the effect, and not the other way on.
The property of a circumstance that (5) it necessitates its effect, although we did not pause to consider the matter, is in a way essential to a final element in a definition of a causal circumstance, more particularly a specification of what is included in such a circumstance. To return again to the beginning, a circumstance (1) consists of items required for the effect. That is not to say that a circumstance includes all such conditions of the effect. Which ones then? The answer is that (9) a causal circumstance is to be taken to include no more conditions than are needed to necessitate an effect. That is, it includes just a set of conditions such that if the set existed, so did the effect, and still would have even if certain other conditions or events had also existed. Nothing is redundant. To take a causal circumstance as having no redundancy is obviously to exclude things wholly irrelevant to the effect. With respect to the circumstance for the starting-to-work of the windscreen wipers, the car's radio being on is likely to be irrelevant.
Other things are not irrelevant in the given sense, since they are required conditions of the effect—but they are not part of the causal circumstance. A caus'al circumstance, in accordance with the non-redundancy criterion, does not include a particular condition and also a causal circumstance for that condition, or any part of one. In specifying a circumstance for the working of the wipers, we may include the switch's being flipped, but if we do, we cannot also include the muscle movements which gave rise to the switch's being flipped. Certainly we do not need to try to go into the whole causal history of an event in order to specify something—one of the many sets of things—that had the property of making the occurrence of the event necessary. In general, if c is in a causal circumstance cc, and c is the effect of cc', then cc' cannot be part of cc and neither can any part of cc'. Equally, a causal circumstance cc for an event e does not include any other effect than e, perhaps an effect in a causal sequence connecting cc with e. To speak loosely, a causal circumstance does not include two or more links of any one causal line running through it from past to future.
We shall have no need of a fuller definition of a causal circumstance than the informal one we now have—given in the nine propositions above. What will be of greater value is a partial characterization which mentions only those features (9, 5, 8, 7, in order of appearance in the partial characterization) which will be of most importance in what follows immediately. Thus, if cc was the only causal circumstance for an event e, then
cc was no more than a set of conditions or events which necessitated e, and preceded e, and was dependently necessitated by e.
As already noted, and as will be of some importance later in this inquiry, the temporal feature does not require that the constituents of the causal circumstance be simultaneous. The point will be of particular relevance in connection with causal sequences or causal chains, to be considered later in the most relevant context. (3.1)
What is bound to come to mind at this point is that there are pairs of things distinct from, but fundamentally like, a causal circumstance and its effect. Certainly the thought must occur to anyone acquainted with almost any part of science, or even a small selection of scientific laws. Such pairs of things enter into what is variously described as interaction, reciprocal causation, functional interdependence, func-tional relation, concomitant variation, and so on. Such pairs of things are like a causal circumstance and its effect in that they stand in fundamental nomic or necessary connection (1.3), which is to say some connection stated by an independent nomic conditional statement. They differ from causal circumstance and effect in that they lack either or both of the features that give rise to the difference between causal circumstance and effect—the priority of the causal circumstance. Thus (i) neither may precede the other, or (ii) they are not such that one necessitates the other while the other merely dependently necessitates it, or (iii) they may lack both features. What is true, rather, is (i) that they are simultaneous, or (ii) each necessitates the other, or (iii) they are simultaneous and each necessitates the other. Such pairs are by definition nomic correlates.
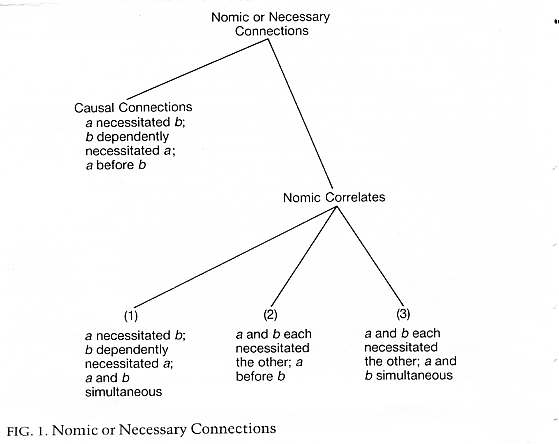
As in Figure 1, then, we have four principal categories of nomic or necessary connection, each involving some fundamental nomic con-nection but differing in some respect from each other category. Each of the three categories of nomic correlates is open to further description, as will be anticipated. For example, with respect to the first category of nomic correlates, the category which will be of most importance to us, there is the truth that if a necessitates b, then b is necessary to a. Also, if b dependently necessitated a, then a was dependently necessary to b.
Certain objections to these conceptions, objections having to do with science, will be considered later. Let me say now only that there is no established conception or usage for 'nomic correlate' or other more or less equivalent terms used in talk of interaction, functional interdependence, concomitant variation, and so on. No doubt, with respect to the first and second categories of nomic correlates, it is possible to call the second member an effect without seeming to misuse language, including this or that scientific language. It is also possible, also without such misuse, not to call the second member an effect, but to call it a nomic correlate instead, as we have. It is on the way to being as reasonable as refusing to say about the see-saw that one end's going down is the effect of the other end's going up. It is reassuring to be able to say that the inquiry to come does not depend on our decision. We shall be concerned with the first category of nomic correlates, and refer to them as nomic correlates, but it is their nature rather than their name that is important.
It will be noticed that in all of this the term 'correlate' is being used in a way consistent with our previous uses of 'event', 'cause', 'condition', 'causal circumstance', and 'effect': not for a type of thing, but for a thing itself, more particularly an individual property or set of such properties rather than a type. To use the term 'event' for a token rather than a type is ordinary. So with 'cause' and 'effect'. 'Condition' and 'causal circumstance' can also be used in this way. The ordinary use of the term 'correlate', where it is ordinarily used, is perhaps for a type of individual rather than an individual. We are departing from this usage, and must put up with some inconvenience, in order to have consistency and hence clarity in several contexts. Nothing substantial hangs on the decision.
One last and related point. We have found causation to consist, at bottom, in connections between particulars. We have analysed the particular statements which state these connections. Some of these, analysed by way of independent nomic conditionals, are in a way general. (1.4) They are distinct, however, from causal generalizations, which will be of some importance in what follows. Much might be said of the relation between particular and general causal statements, but here a little must suffice. If we maintain that cc was a causal circumstance for e, we are maintaining the conditionals of which we know, notably that if cc occurred, then even if certain things of a general class had also occurred, e would still have occurred. This is evidently in a way general. By asserting it, however, we are also committing ourselves to a general conditional proposition of a standard kind. We cannot make the causal claim about cc and allow that other circumstances identical with cc have different upshots. If we take the starting of the wipers to be an effect of a given circumstance, we must accept that there is a type of circumstance which is connected with startings of wipers generally. What is true, to express the matter simply, if cc was a causal circumstance for e, is this:
If any circumstance of the type of cc occurs, even if certain other events or conditions also occur, so does an event of the type of e. If the event does not occur, neither does the circumstance.
We are committed to other such generalizations, less simple, one of them related to the fact that a circumstance is dependently-necessary to the occurrence of an effect. We are similarly committed in connection with nomic correlates.
1.6 THE VIEW DEFENDED
1.6.1 Causation and Science
What has been implied in this inquiry, and what it is natural to think, is that a conception of causal and other nomic connections is fundamental to, and pervasive in, our view of reality. If that is so, it constitutes a general reason for the ordinary and perhaps irresistible belief that reality is in whole or in part a matter of causal and other nomic connections. That ordinary belief in turn gives some support, to say no more, to theories of determinism pertaining to our choices and actions: theories whose burden is that we in our lives are a matter of such connections. The strength of the general reason for the ordinary belief depends partly on the resolution of large philosophical issues. These, having to do with whether we take our concepts from or to reality, will not be debated here.
Still, I do not wish in what follows to forego the support of what must seem to be the good sense of our natural empiricism, which is independent of philosophy. (It gets definition of a kind by way of the firm rhetorical question: 'If we do not get our conception of causal and other nomic connection from reality, where do we get it?') That is one reason for looking at a certain objection, that our conception of such connection is not fundamental to, or pervasive in, a certain body of knowledge and speculation, one which must have some pride of place in any informed view of reality. The body of knowledge and speculation is science.
There is also a larger reason for considering the objection about the place of causal and other nomic connections in science. It is that the particular theory of determinism in the chapters to come will depend considerably on the claim that the part of science most relevant to it, neuroscience, does indeed establish certain causal and other nomic connections. This could hardly be so if a conception of such connections was no part of neuroscience.
The objection in one audacious form is that science has or should have nothing to do with causation. Russell took this view at one point (1917a), giving a mixed bag of reasons. Most of them, in retrospect, are poor. (Mackie, 1974, Ch. 6) We will do better to consider the objection that science does not in fact involve or make use of a conception of causal and other nomic connection. What prompts it is the truth that many of the general propositions fundamental to science, most notably many of those dignified with the name of laws, are not of the form of ordinary causal generalizations or ordinary nomic but non-causal generalizations. That is, they are not of the form exemplified at the end of the last section when it was said that if cc was a causal circumstance for e, then there is the true generalization that all circumstances of the type of cc, even if certain other events or conditions occur, are followed by events of the same type as e.
There are several differences. The fundamental one is that as a result of the mathematization of physical science, what importantly occurs in it are equations or formulae of several kinds, propositions to the effect that one set of magnitudes is related in a certain way to another set or sets. More particularly, they assert in several ways that values of one variable or parameter are a certain function of values of other variables or parameters. The theory of mechanics, for example, consists in equations which specify that certain traits of bodies in motion are dependent on other physical properties. Is it then the case that no group of these fundamental quantitative propositions of science can be interpreted as stating causal connections? On the contrary, some can, and have often been called and regarded as causal laws. The subject is a large and complex one, but the essential point is simple, and easily illustrated.
The point is that an equation can be interpreted as stating this: given each of a number of possible extents to which specified things possess :ertain different general properties, it is then the case, despite accompanying conditions and events, that another specified thing would still possess another general property to one of a number of possible extents. That is, the equation can be causally interpreted, by way of a conditional of the sort we know. It is different in being numerical and in its generality. It is general in two ways. It has to do with general properties, certainly, but also it has to do with ranges of them.
To return to one of our initial examples, consider the belief that it is the position of the car's heater that accounts for the driver's left knee being warm. In believing this we believe that some causal circumstance necessitated the temperature of his knee. We could by measurement give a numerical specification of each of the parts of the causal circumstance—the operation of the heater, its relative location, and so on—and also such a specification of the effect. Or rather, we could replace our imprecise proposition with a precise one, numeric-ally expressed. A further step, or rather a great deal of research, would be greatly more significant in terms of the question we are considering. This would bring us to something akin to the fundamental prop-ositions of science. We could replace what we have with a proposition relating variation in the operation of the heater, variation in its relative position, and so on, with variation in the temperature of the driver's knee. This generalization would of course be efficiently stated only by way of a certain interpreted equation. The equation would involve .. both time and a many-one relation, the marks of nomic connection of the causal kind.
The moral of this simple reflection is that fundamental propositions of science can be and often are causal, despite generality and mathematical form. It is difficult to see why it has ever been supposed otherwise—that generality and number in themselves somehow fight with causation sensibly conceived. The simple reflection also illus-trates something else, that the fundamental general causal prop-ositions of science rest on particular causal propositions, of a kind with which we are all familiar.
None of this, of course, is to be confused with the idea that all of the causal laws of science, or even many, are in the given way analogues in form of the ordinary belief that a particular causal circumstance necessitated a particular effect. That is, roughly, they do not assert that variations in a fully specified type of causal circumstance are followed by variations in a type of effect. There are many alternatives. Some equations, asserted in a certain context or on certain assumptions, have to do with parts of causal circumstances. Others relate (i) what would ordinarily be called an effect and a part of a causal circumstance to (ii) another part of the circumstance. All of them have theii foundation in the basic connections between causal circumstance ana effect, above all that causal circumstances necessitate their effects.
The idea that science does not involve causal connection also faces other difficulties, one of which can be given briefly. It is possible, through concentration on parts and aspects of science, or by way of the refutable assumption that the word 'cause' does not turn up in it (Suppes, 1970, pp. 1-2; cf. Skyrms, 1980, p. 110 f.; Hesslow, 1981), to forget that science includes a vast number of propositions which are in various ways explicitly causal. For example, this is true of classifi-cations and definitions, which typically involve causal conceptions. To anticipate something to come in this inquiry, an ordinary definition of the neuron is an example.
"A special type of biological cell, being the unit of which the nervous systems of animals are composed. It consists of a nucleus surrounded by a cytoplasm from which thread-like fibres project. In most neurons impulses are received by numerous short fibres called dendiites and carried away from the cell by a single long fibre called an axon. Transfer of impulses from neuron to neuron takes place at junctions between axons and dendrites, which are called synapses." (Uvarov, Chapman, and Isaacs, 1979)
So much for the claim that science does not involve causation. The other part of the objection (p. 50), that it does not involve other nomic connection, is as mistaken. In fact, philosophers and others who have been sceptical about the place of causation in science have been inclined to put non-causal nomic connections, somehow conceived in its place, (i) Connections of this kind are stated in, among others, laws which enter into the taxonomical classifications of 'natural kinds' or 'substances'. Such laws assert connection between determinate proper-ties in every object or stuff that is of a certain kind—arsenic, benzopyrene, coal, and so on. (ii) Non-causal nomic connections are also stated, as remarked at the beginning of this chapter, in numerical laws such as the Boyle-Charles law for ideal gases, pV = aT, where p is the pressure of the gas, V its volume, T its absolute temperature, and a a constant pertaining to the mass and nature of the gas. (iii) Lastly, non-causal nomic connections are stated by numerical laws different in that they do specify how a magnitude varies with time. Galileo's law for freely falling bodies in a vacuum is an example. Such laws, although sometimes run together with causal laws, are best regarded as otherwise. This is so since the relation of dependence between the variables given in the law is wholly symmetrical: a later state of a system fixes an earlier state as much as an earlier fixes a later.
The necessary qualifications in the case of each of the three sorts of jon-causal connection are many. To mention only the most general one, the non-causal connections asserted within science are of many diverse kinds, and they are usually in one way or another partial. They do not assert, simply, that x is a nomic correlate of y. It is usually the case that what is specified, against a certain background assumption, is a part of the nomic correlate of something else.
All of this has been set out in greater detail before now. (Feigl, 1953; Nagel, 1979; Mackie, 1974; cf. Bunge, 1959) A good deal of illustration of both causation and other nomic connection in science will be provided in due course (Ch. 5), when we consider neuroscience. What remains to be said here is that the objection—that science does not involve causal and other nomic connections—is sometimes a part of something more general and by its nature more difficult to deal with: scientific scepticism about philosophy and its categories.
If this scepticism has often been well-based, an all-encompassing and undiscriminating scepticism is absurd. (One occasionally encoun-ters a burst of inanity of Nobel proportions, as in this: 'Our capacity for deceiving ourselves about the operation of the brain is almost limitless, mainly because what we can report is only a minute fraction of what goes on in our head. This is why much of philosophy has been barren for more than 2,000 years and is likely to remain so until philosophers leam to understand the language of information processing.' (Crick, 1979, p. 132) The language is not so hard to understand, and it is jejune to suppose that not knowing it has impeded philosophy, or that knowing it will help a lot.) It needs to be kept in mind, by both science and philosophy, that the concerns of the two are in large part different. A general account of nomic connection is an aim of philosophy but no more an aim of science, despite the fact that it rests on such connection, than, say, a general theory of prosody is an aim of poets. Nor is science concerned with just the kinds of generalization that make up a theory of determinism with respect to our lives. The latter have a scope suitable to the question in hand. Different concerns and procedures, and hence unfamiliarity, should not be allowed to stand in the way of understanding.
7.6.2 Specifying Causal Circumstances
A second and commodious objection to the view of nomic connection which has been set out was anticipated earlier (1.3), and may be shored up a bit by the fact lately mentioned, that science broadly speaking is not much engaged in arriving at complete descriptions of causal circumstances—causal circumstances as we have conceived them. Rather, as was mentioned, it is concerned in several ways with parts of such circumstances, often enough a single condition.
The objection is that neither in science nor elsewhere do we in fact have or use the conception of a causal circumstance that has been set out here. It is accepted that some conception of a set of conditions for an effect is used, but it is denied that this is the conception of a causal circumstance. That, as may be said in tones suitable to the objection, is the conception of something so complete as to necessitate by itself its effect. More precisely, it is the conception of something which has the nature assigned to it above all by the independent nomic conditional (5). Thus, in part, a causal circumstance is such that if it occurred, then even if there also occurred any change logically consistent with it and its effect, the effect occurred—or, it was the first and the effect was the last of a sequence of things such that the given connection obtained between each thing and its successor. To speak in the same right tones, a causal circumstance can be said to comprise everything needed so as in a way to guarantee its effect. It is such that nothing could get in the way of its operation save changes logically inconsistent with it or with its effect or with a causal sequence of which it and its effect are parts.
The objection, again, is that we do not in our standard causal thinking have or use such an idea. Certainly we have and use some lesser idea of a set of conditions and events for an effect, including what we call the cause, but we do not have this ambitious idea. The objection involves the feeling or perhaps the conviction that we can never state or explicitly describe such a thing as a causal circumstance is said to be, which is to say that we cannot do something like give a complete enumeration of its elements: we cannot give particular or individuating descriptions of all of them. (Cf. Russell, 1917a, p. 187; Lucas, 1962, pp. 57-9; Scriven, 1964, p. 409)
For illustration, consider a staple example in thought about caus-ation, that of a house fire, caused by a short circuit. The view to which we have come is that the cause was part of a causal circumstance as conceived. But, it is maintained, we cannot state this circumstance. We may make an easy start with the short circuit and a bit more, but do we not then have to include in the circumstance the absence of a burst in a water pipe at the right moment? Do we not have to specify the particular condition which was the absence of a torrential rainstorm and an open window? Do we not have to include there having been no general power failure in South-east England, and the absence of an earth tremor that would have shifted whatever it was that first ignited, and the earth's not being destroyed by a nuclear explosion? And so on. To state the relevant causal circumstance, would we not have to do what we can hardly hope to do, which is to enumerate parts of much of the whole state of the universe at or during a time? In fact, it may be added, we do not take ourselves to be faced with such an overwhelming task in connection with condition-sets for an effect, and hence for this reason too those sets are wrongly conceived as causal circumstances.
The objection touches on large issues in the philosophy of language and in epistemology, but a relatively brief reply, distinguishing various lines of thought that enter into it, is certainly possible.
The first is that we do not have a certain general idea, since often we do not have certain specific ideas. One thing to be said of that is that it does not at all follow, from the fact that we cannot give particular descriptions of items that fall within a set, that we cannot satisfac-torily conceive of and describe the set. (The measure of what is satisfactory will, as always, be fixed by a given practical or theoretical purpose.) No one can enumerate the conditions and events which issued in the first sighting of Halley's Comet or the weights of man-made objects in the Northern Hemisphere in the nineteenth century, but it would be bizarre to say that no clear ideas attach to those definite descriptions. It is as bizarre to suppose that I do not have a clear idea of a particular causal circumstance, say the one which gives rise to a query on the console of my computer, when I am unable to enumerate its elements. Of course the description I can give is general. But if the general were the unclear, we could with reason abandon all science and inquiry.
The objection in another part is that in order to confirm an hypothesis that an effect was in fact the effect of a causal circumstance of a certain type, we do need an enumeration of elements, and often we do not have an enumeration. We shall be unable to test an hypothesis unless we have a close specification of the circumstance-type, and often we lack it. That is true, but it does not issue in the conclusion that we do not ordinarily have and use the given conception of a causal circumstance, or that we could not use it in the confirmation of causal hypotheses. The fact of the matter is. that we do not often have confirmed hypotheses of the given kind. In our day-to-day lives, including day-to-day scientific lives, we have little need of such confirmed hypotheses. The situation is not that we always have confirmed hypotheses, and sometimes or often lack an enumeration of the elements of a causal circumstance. If that were true, it would perhaps support the conclusion that a different conception of a condition-set for an effect enters into our beliefs and proceedings, although that is unclear. But it is not true.
In a third part, the objection must be that with respect to confirmed hypotheses as to condition-sets, it cannot be that those condition-sets are causal circumstances as conceived. Causal circumstances as conceived are unspecifiable. This central line of thought takes its force from overlooking an essential specification of a causal circumstance, one which derives directly from our ordinary beliefs.
Suppose we say that the causal circumstance for the house fire consisted in the short circuit, the location of inflammable material in contact with the relevant conductor, and the presence of oxygen. We could try harder and do better by specifying certain electrical facts, an ignition temperature for a material, and so on—in general by giving conditions for the particular chemical reaction of combustion that occurred—but there is no need. It is of course true that each of the three elements in the circumstance as described was itself an effect of something else, and, further, had a whole causal history. No general power failure in South-east England and no nuclear explosion were indeed part of the history of the short circuit. But a causal circum-stance, as specified earlier (p.46), most certainly does not include all of the causal history of itself and hence of the effect. As specified, a causal circumstance includes no more than was needed to necessitate the effect, which is to say that it included just a set of conditions or events such that if the set existed, so did the effect, and still would have even if certain other conditions or events had also existed. The causal history of anything includes innumerable causal circumstances—none of them, however, includes any of the others. Thus the enterprise of confirming what was a causal circumstance for something else is not remotely like some hopeless speculation into the whole natural history of a thing, or even a stretch of it.
In a fourth part the objection takes some strength from the truth that, as in this case, our conceptions of particular causal circum-stances, by certain possible comparisons, are inadequate. It is indeed true of the given description of the causal circumstance for the house fire that it could be much improved. But it also possible to think, with respect to any improvement, that it leaves room for further improve-ment. We may forever want confidence that we have come to the ultimate facts about some physical process. That is not to say we have no satisfactory conception of the particular causal circumstance. Or, if it is to say that, by way of some stringent idea of what is satisfactory, there is also another conclusion to be drawn. It will be along the lines that it is quite as true that we have no satisfactory conception of anything much—including, most piquantly, the elements which enter into any alternative conception of the condition-set for an effect. As elsewhere, a too zealous objector is hoist by his own petard.
Fifthly, to introduce something not so far mentioned, the objection may include the idea that if our causal thought did rest on the given conception of a causal circumstance, we should be able to do well at prediction—better than in fact we do. Causal circumstances in a way guarantee their effects. But it does not at all follow from the fact that causal circumstances in a sense guarantee their effects that we can predict those effects better than we do. To do so we would require knowledge which in fact we lack.
1.6.3 Condition-Sets and Backgrounds
The objection just considered is linked to another, or rather, to a positive proposal as to condition-sets and their effects. We may be told that what we understand of an event e, if it is taken as an effect, is that there existed a certain set of conditions—say sc—such that since it existed, e occurred, and e would still have occurred so long as 'the usual background' or 'the usual environment' obtained. It is therefore allowed, although e was an effect, that we might have got sc along with some extraordinary event or condition, and not got e. (Cf. Mackie, 1965, p. 250, 1974, Ch. 2; Lucas, 1962. pp. 57-9; Scriven, 1964, p. 409; Anscombe, 1971, pp. 1, 12, 23; Kenny, 1975, p. 110, p. 115.)
We are to understand that the idea of a usual background is relative: there are different usual backgrounds for different causal claims, or different groups of causal claims. With respect to the short circuit and the house fire, it is true that since a set of conditions obtained, there was the fire, and this would still have occurred so long as, say, there was not a flood at the right moment. The usual background does not include a flood. It is allowed, as it must be, that the idea of a usual environment is vague, and hence that our ordinary causal beliefs are vague.
A set of conditions of the given kind, one which is followed by the effect if the usual background obtains, is called by some philosophers a sufficient condition for the effect. Given what is said of the need for an ordinary background, the condition-set is of course not sufficient for an effect in an ordinary sense, where a sufficient condition is precisely one that necessitates the effect. The fact is recognized by some philosophers who take the given view of causation. They note in using the term 'sufficient condition' that they do not mean that the condition-set is genuinely sufficient for the occurrence of the effect. It is partly because 'sufficient condition' and 'causally sufficient condition' are so used, incidentally, that I have introduced the term 'causal circumstance'.
There is something more important, which is that the essential idea of the background view does not in itself conflict with our necessi-tation view. Those who propound the background view deny or doubt the necessitation view, of course, but they need not. We can in fact accept it along with our proposition that effects are necessitated events. We then have the composite view that an effect is necessitated by a causal circumstance and, furthermore, is related to a so-called sufficient condition in the way described, having to do with the usual background. It may be that there is something to be said for this composite view.
Can the background view be held on its own as an adequate account of causation? So it is supposed. However, there seems to be very strong reason indeed to think that there cannot be an acceptable account of effects as we conceive them which does not include necessitation.
Suppose a radical objector says of an effect, the smell made by the candles when they were snuffed, that there existed no circumstance such that no matter if certain other events or conditions occurred, the effect would still have occurred. He does not supplement but instead denies the view of causation to which we have come. The objector must be disinguished sharply from someone who merely attributes to us some particular idea of a particular necessitating circumstance for the effect, some particular idea of what was included in the circum-stance for the candle smell, and believes that the circumstance included more. (The latter person merely maintains of a particular set of conditions that it was not the whole of the causal circumstance. It would not have been followed by the effect if some other event or condition had been missing.) Our radical objector maintains about what we take to have been the causal circumstance that it might not have been followed by the smell, and moreover that this would not have resulted from the absence of some further condition. He thereby makes what happens, the smell, into what can properly be called a matter of real chance. He maintains that what we take to have been the causal circumstance might have existed as it did, and the rest of the universe might have been just as it was—and there might have been no smell.
It is important to allow that he may be right about one thing. At any rate, we have no need to dispute one proposition. Things might have happened just as he says. Causation or some of it might have come to an end just when I set out to snuff the candles, or never existed. Despite what has been said (p. 50) about an inference from our conception of causation to a conclusion about the nature of reality, our present concern is that conception. We are not engaged in proving the universe to be nomic, or defying it to step out of line. We are examining one of our fundamental conceptions of it. It is a conception that might not be true of it, or all of it, and which might cease to be true of it or of all of it.
What our radical objector cannot maintain, if he sticks to his guns about the relation of the smell to what went before, is that the smell was an effect. He says that the circumstance might have existed as it did, the other events and conditions in the universe might have been as they were, and there might have been no smell. If this is so, the smell was not an effect. The connection between the circumstance and the smell was fundamentally unlike the connection which we take to hold between a causal circumstance and its effect. The connection between the circumstance and the smell, on his view, is precisely the kind of connection, or want of connection, that would be true of real chance or real random events.
It does not matter if our objector allows or insists, as no doubt he will, that it was in some consistent sense probable or highly probable that the smell would occur. It is also true, on his view, for all this probability, that it might not have. On his view the fact that it ceased to be a probability, and did occur, is something that might not have happened. Obviously no addition about background conditions, as understood above, will help.
There is another expression of this reply to the radical objector. It depends on the fact that standard effects are events which in the most fundamental sense can be explained. There is a theoretical possibility of explaining them. We are not here concerned with the elusive though connected fact that causal circumstances in a different sense explain their effects, that sense which concerned us earlier in connection with causal priority. To say that effects are events which in a fundamental or standard sense can be explained is to say this: there is a possibility of our finding a proposition which fully answers the question of why they occurred. Effects are such, on the view of causation to which we have come, since there is the possibility of finding those things which no matter their accompaniment would still have been followed by the effect. However, what we surely have on the objector's view is precisely that the smell of the candles was something that cannot possibly be explained. I do not mean, of course, that it was something that cannot be explained yet, but rather that it was something of which no explanation can conceivably be found. No fundamental or standard explanatory proposition is possible. This is so since in yet another sense of the term 'explanation', there was none. There was no such thing in the world. There was no thing in the world for an explanatory proposition to state. What we are supposing is that everything could have been exactly as it was except for the non-occurrence of the smell of the candles. Hence there is nothing that explains what in fact did occur.
It needs to be allowed that this reply is of a certain kind. The objector has it that what we taken to be effects need not be necessitated. The reply has been that this converts effects into what they are not: chance or random events, and inexplicable events. However, definition of these latter events perhaps must be that they are unnecessitated events. The reply, then, it can be said, does not make use of a feature of effects independent of their being necessitated events, which feature can be used to argue that they are necessitated events. The reply, however, consists in more than mere reiteration or insistence. It is, at bottom, that beyond doubt we use certain ways of speaking in connection with effects. They are not random and not inexplicable. It can be added that they are not mysteries, not discontinuities, not small or large miracles, and so on. It may be that these ways of speaking can be explicated at bottom only by way of the idea of necessitation. What is indubitable is that they are used of effects, that they cannot be used of unnecessitated events, and hence that effects as we understand them are not unnecessitated events. There is more to be said, but it will be better said in reply other related objections.
1.6.4 Causes as Merely Required for Effects
We have concluded that a standard effect—one that is not a decision, choice, or the like of a person, or a following action—is indeed taken to be an event necessitated by a causal circumstance. To speak of a standard effect is to speak of an event necessitated by a circumstance, and to imply the existence of such an effect by speaking of a cause is to imply the existence of a necessitated event. Necessitation, of course, is simply the fact of the connection stated by the independent nomic conditional (5). It needs particularly to be kept in mind, with the objection now to be considered, that it is indeed advanced as an objection to a given analysis of our causal beliefs, and hence is itself a proposal as to those beliefs. That is why it is now of interest to us. It is not unknown for a philosopher or scientist, lured by the song of the sirens, which is to say an interpretation of Quantum Mechanics, to drift off course to a proposal as to a better or improved conception of causation. That one conception is somehow better than a second, supposing that that can be made out, is of course not the proposition that it is our conception or one of them.
The objection is that it is enough, for something to be a cause, that it is required for the occurrence of another event. It is enough, for an event to be a standard effect, that something else was required for its existence. It is enough if the dependent conditional (1), or perhaps one of the variants (la) or (Ib), is true of the two things. Consider an indeterministic coin-in-the-slot machine. (Mackie, 1974, pp. 40-43; cf. Feynman, 1967, p. 147; Anscombe, 1971; Sorabji, 1980, Ch. 2; Mellor, 1986) A coin is put in and a chocolate bar comes out. If the coin had not been put in, the bar would not have come out—the first thing was required for the second. However, the bar might not have come out even though the coin was put in. This failure with this surprising machine would not have been at all like the failures of ordinary deterministic coin machines. We are not to suppose of this machine that when a chocolate bar does not come out there exists a causal circumstance which necessitates the failure. Nor, on the present occasion when the machine does produce a bar, is there a circumstance that necessitates that. Given that the coin was put in, it was then a matter of what can be called real chance that the bar came out. But, it is said, we would say of the bar's coming out that it was an effect, and in particular the effect of putting in the coin. Therefore no more is needed for an event to be an effect, at least in so far as relations of conditionality are concerned, than that the event was such that another one was required for it.
This opinion can seem persuasive for a time, but we cannot persist in it. Let us not lose hold on the essential proposition that the machine is indeterministic. It contains a mechanism, perhaps a Quantum Mechanical mechanism or what is as fairly called a mystery-mechanism, such that everything might have gone on just the same up to some instant, let us say the instant when the bar appeared, and it might have happened instead at that instant that no bar appeared. It is not that something, anything whatever, would have been different before that instant if the bar had not appeared. The coin would have been put in, and so on. There was no necessitating circumstance whatever for the appearance. There would have been none whatever for the non-appearance if that had happened.
What may lead one towards supposing, despite this, that the bar's coming out was an effect of putting in the coin, is a certain fact. It is that the coin was indeed a perfectly ordinary cause of something, which thing was not a thousand miles away from the bar's coming out. The coin caused it to be possible that the bar come out. If that sounds a touch mysterious itself, it only sounds so. What we can say instead, unmysteriously, is that putting in the coin, like every other putting-in of a coin, activated the indeterministic mechanism. But the fact that the coin caused the mechanism to operate is no reason for saying that the coin caused the bar to come out. What we will say, if we keep clearly in mind that everything might have been the same up to the instant when the bar came out, and no bar might have come out is that nothing caused the bar to come out. We will say that exactly what did not exist was a causal link between the operation of the mechanism, or anything else whatever, and the bar's coming out. The temptation to say the coin caused the bar to come out can be explained by seeing it for the ordinary cause that it was, and of what event it was the cause, and of what nearby event it was not the cause.
The objection as used by one philosopher (Anscombe, 1975) is embedded in further reflections. All of them, to my mind, are ambiguous. It is unclear whether the subject-matter is our beliefs as to causation, or the truth of those beliefs. That is, it is unclear whether what is being maintained is that our conception of effects is of unnecessitated events or that we should change it to that. One of the reflections is that we believe circumstances to be 'enough' to make their effects happen, which is consistent with their not happening. (Anscombe, 1975, p. 60) No argument is given. Nor is any suggestion made as to what we presumably also believe about a difference between a circumstance which was enough to make an effect happen, but didn't, and a circumstance which was enough to make its effect happen, and did. If we had the given conception of 'now-they-work-and-now-they-don't' circumstances, we presumably would also have an idea along these lines that might be reported. It would of course be precisely different from the idea that a complete causal circumstance produces its effect and an incomplete one doesn't. It would in fact be a pretty salient idea, since we would have a lot of use for it, on many unhappy occasions. It is my view, of course, that we have no such idea, and no need of it, since we do not take condition-sets for effects to be merely 'enough' for them in the given sense.
1.6.5 Non-Standard Causes
There is another possible argument, which can be dealt with quickly, for the conclusion that standard effects are no more than events for which other events are required. It relates to the very distinction between standard and other effects, and depends on what that distinction grants, that we sometimes speak of decisions and the like as effects without supposing that they issue from causal circumstances, which by definition are necessitating circumstances. (1.3) The possible argument consists in the premiss (1) that decisions and the like are taken to be effects but also to be no more than events which follow on conditions which are required for them, the further premiss (2) that it is to be presumed that we have a single conception of effects rather than several, and the conclusion (3) that all effects, including what have been called standard effects, are merely events preceded by conditions required for them.
Although I have earlier granted it to simplify matters (p. 21), premiss (1) is not nearly so firm as an objector might like. Certainly we often think and speak of decisions and the like as effects. 'In the end, what made him decide was the thought that time was running out.' 'Her choosing that wine was the effect of what you said about its edge.' In such cases, we do indeed seem to take decisions and choices as having required conditions. Do we also take them to be necessitated? Well, our usages do strongly suggest that this or that thought or feeling completed a set of thoughts and feelings, and the decision or choice resulted. The thought or feeling tipped the balance, made the difference. The decision or choice issued from a completed circum-stance. However, a commitment to Free Will somehow understood, or the force of some image of Free Will, is likely to keep many of us from the further conclusion that the circumstance was exactly a necessi-tating circumstance. But if we do clear-mindedly and explicitly take decisions not to have necessitating circumstances, do we call them effects at all? I am inclined to doubt it, but let us not linger, and consider instead the second premiss of the argument.
It is that we have a single conception of effects, rather than several. On what is this based? In fact there is no established generalization about our concepts, or our fundamental concepts, on which it can be based. It would be exceedingly difficult even to formulate one. In all of what conceptual situations, so to speak, is it to be supposed that we have a single conception rather than several related ones? Certainly it is not to be supposed of all situations: for a start, we do not have a single conception of truth but rather at least two conceptions, those of analytic and synthetic truth. Putting aside the idea that there is an established generalization of the right kind, we might wonder if there is something related: a sound principle of inquiry, a presumption or guide to be followed for the most part. This would give us a weakened form of the argument we are considering. One response to this is, in part, a concession. Often, or at least sometimes, it is not a good idea to multiply senses. That, however, falls very short of something to be dignified as a principle of inquiry. A principle of inquiry cannot be something that may keep us from recognizing a clear and settled conception.
We do have a clear and settled conception of standard effects. We do not suppose that the wipers' starting to work was some sort of accident or mystery, of which the driver's flipping the switch was merely a required condition. We suppose the starting-to-work to have occurred necessarily. There is no need to say more of the argument. There is the sweet temptation to add, however, that there is a bad but better argument of the same form. (1) We take standard effects to be necessitated. (2) We have a single conception of effects. (3) We therefore take all effects to be necessitated.
1.6.6 Probabilism
The last sort of objection, perhaps more than the others, consists in certain alternative views. It is these views in particular that involve the ambiguity mentioned earlier, (p. 61) That is, they tend to move between a claim as to how we do in fact conceive of causation and a recommendation as to how we ought to conceive of it. The recommen-dation is partly based on the feeling or belief, owed to Quantum Theory, that universal determinism or the Law of Causation is false. The official business of these essentially philosophical rather than scientific views is and must be the first or conceptual matter, the analysis of our conception of causation. It is only so understood, certainly, that they are relevant to our present business. So understood, they share the idea that we, or many of us, take effects to be no more than probable events. (Suppes, 1970, 1984; Skyrms, 1980; Mellor, 1986) Some of these events are certain, or, to speak in terms of the Probability Calculus, have a probability of degree 1. More of them, however, have a lesser probability. According to most of these views, although they wisely do not parade the fact, effects may have a probability of 0.5 or indeed less. In what follows, I shall not reproduce the details of any of them, but proceed more generally and schematic-ally.
It may simply be said that what is needed for two events to be cause and effect as we understand them is that the probability of the second, given the first, is higher than the probability of the second, given the absence of the first. Or, it may be said, two events are cause and effect if the conditional probability of the second—its probability con-ditional on the occurrence of the first—is greater than the uncon-ditional probability of the second, which is a probability independent of whether the first occurs. Or, finally, two events are cause and effect if the probability of the second event, given the first event and certain accompanying conditions, is greater than the probability of the second event, given those conditions but not the first event.
As they have just been inexplicitly stated, each of these views is in fact itself better regarded as a set of possible views. The members of each set are distinguished one from another by what are fairly well known, the different theories of the nature of probability, all of them consistent with the Probability Calculus. There is no agreement as to how many of these there are, partly for the reason that there is no clear principle of counting for such theories, and no full agreement as to what, from some point of view, are the theories worth considering. (Mackie, 19730; Weatherford, 1982; Benenson, 1984)
One thing said in support of the idea that we take effects to be probable events, and, more particularly, said against the analysis expounded in this chapter that we take them to be necessitated events, is relevant enough, although likely to be disdained by the high-minded. It is a diagnosis whose burden is that the supposedly mistaken analysis, of a kind which has persisted through centuries, is owed not to good reason but to a kind of desire. It now, persists, it may be said, because of a non-rational or irrational longing on the part of philosophers to have order in the universe, a longing that has replaced the lost comfort of a belief in an all-governing God. (Cf. Suppes, 1984, pp. 1-2, 17, 29, 51.) The proper reply to this is not that the truth of a view, strictly speaking, is independent of the motivations of those who hold it, although that is so. The proper reply, which accepts the fact that we may rightly have some suspicion of a view on the ground that its proponent wants it to be true, is that the satisfactions afforded by indeterminist as against determinist claims of one kind and another are far greater. The point is worth considering for a moment, partly because it is of relevance to greatly more than the present conceptual issue.
The first satisfaction of indeterminist claims, including those, like the present one, which are not within but are antecedent to the traditional area of dispute about Free Will, is of course that they leave, or promise to leave, room for a reassuring or enhancing view of ourselves and our situation. One proponent of effects as unnecessitated does not speak only for himself. 'I cannot say that I think of [the causal determinist's view] as having any plausibility. And I should certainly hope that it was false. For I believe that it is determinism that rules out moral responsibility and other things we believe in . . .' (Sorabji, 1980, p. 37) Another would-be defender of freewill is as explicit. 'Without freewill we seem diminished, merely the playthings of external causes. Our value seems undercut. . . . My concern is not only intense but directed. I want (to be able) to conclude that we are worthwhile and precious.' (Nozick, 1981, p. 2)
A second satisfaction of indeterminism is in some relation to the first. It is the wider satisfaction of a universe which is precisely not subject to order, but has in it uncertainty, novelty, and escape from the past, all somehow agreeably constrained by probability.
Thirdly, and perhaps most relevantly to our present concern, there is the more intellectual satisfaction to be had from extending, the application or province of a favoured doctrine, theory, or calculus, perhaps something in which one has a proprietory interest. Here it is incidental that the doctrine or whatever conflicts with or does not fit in well with determinism. The thought must indeed come to mind with probability theory and the Probability Calculus, and their being imported into causation, despite what was said above about the logical consistency of probability theory and necessitation.
Fourthly, there is the satisfaction of a kind of orthodoxy, perhaps with respect to what is taken as somehow of the greatest significance or fundamentality. An interpretation of Quantum Theory comes to mind. For this and the previous three reasons, it is not difficult to conclude, at least tentatively, that more inclination is satisfied by indeterminist than by determinist claims.
The general subject of determinism and our inclinations, however, is that of a companion volume to this one, The Consequences of Determinism. The idea now under consideration, that we take effects to be probable events, is announced or expounded but not much supported by argument. The explicit arguments of which I know are to my mind hopeless.
"... the everyday concept of causality is not sharply deterministic in character. All of us have said things like . . . 'His reckless driving is bound to lead to an accident'. What we mean ... is that the probability of the person's having an accident is high, and his own manner of driving will be at least a partial cause of the accident. The phrase 'is bound to' means that the probability is high of his having an accident. The phrase 'lead to' conveys the causal relation between the reckless driving and the predicted accident." (Suppes 1970 p 7. cf Suppes, 1984, p.54)
The claim or premiss reduces to this: that we often say and believe something is likely to cause something else. But that truth is wholly distinct from, and does not entail, the proposition that the connection we take to hold between cause and effect is one of probability. It is not too much to say that the quoted argument has the strength of this- We say it is probable that the spoon is under the napkin; the relation of 'being under' is therefore a relation of probability.
What gives what persuasiveness it has to the probabilistic idea about causation is neither such an argument for it nor the earlier diagnosis of the appeal of the opposed view about necessitation. It is that the probabilistic idea is in accord with a kind of empiricism. This is an empiricism related to kinds of positivism and to operationalism. It amounts to a determination or tendency to accept as conceptually respectable, and as a report of reality, only what is in accord with some part of scientific practice, or a fully specified calculus, or particular and explicit scientific laws, or particular kinds of quantification, or some principle in the philosophy of science. Since considerations of probability are to the fore in one part of actual scientific practice bearing on causation, and there is little attempt to go beyond them, and there is to hand the Probability Calculus, we are invited to take it that causation can come to no more than probability.
This empiricism, which is indeed preferable to paradigmatically unscientific excesses of speculation and the like, is nevertheless wholly inadequate, and generally accepted to be such. It can be no more tolerable than one of its most specific forms, behaviourism in psychology, (p. 73) That particular movement, essentially the at-tempt to reduce the facts of mentality to the measurable facts of bodily movement, has rightly collapsed. To come closer to our present concern, there is no more hope for the idea that a certain determinism is false because we do not aspire to prove it, but rather proceed in several alternative ways, including probabilistic ways, on the assumption of its truth.
"Ordinary observation and participation in physical phenomena seem to areue decisively against nature being deterministic. Causal attention to the way that a breeze moves the leaves on a tree would seem to make it quite unrealistic to think of having a theory that could predict their motion. ... To think that one could actually predict these phenomena, that there would ever be a possibility to do so, seems on the surface quite mistaken. It would indeed take something close to theological commitment to think otherwise." (Suppes, 1984, pp. 12-13)
It does not begin to follow, from our having no effective theory or practice for predicting breezes, that they are not necessitated phenom-ena. To return finally to our present conceptual concern, it does not follow either, from the fact that in parts of science there is a dependence on probability, that the subject-matter is not conceived in terms of necessitation. If the empiricism in question has the attraction of method and restraint, at least when compared with certain other things, it is not something in which anyone, including its proponents, can persist.
There is more to be said against the probabilistic analysis of our conception of causation that can or needs to be said here. (Papineau, 1985a) I shall content myself with little more than some comments.
(i) Proponents of probabilistic analyses have it that two events can be cause and effect if the presence of the first raised the probability of the second from 0 to only -01, or of course less. That is, the second can be an effect of the first if the first left the second, to speak in ordinary terms, very highly improbable. The same will be true, presumably, of the causal condition-set for the effect. The thought may come to mind of stipulating, say, that a cause or condition-set made an effect more probable than not—that is, gave it a probability of 0.5+. The arbitrariness of this would be extreme. Further, it could not be supposed this is what we now believe. If it were, we should be subject to a kind of indecision about the causal connection between condition-sets and their effects which is in fact entirely missing from our deliberations.
(ii) On the given probabilistic analyses an event e, if it lowers the probability of an event f, cannot be cause of f. But an event which lowers the probability of a second event, on the informal or any other theory of probability, may in fact turn out to cause it. Some medicines have caused precisely what they were rightly judged likely to prevent. (Hesslow, 1981)
(iii) There are the greatest difficulties in fitting the particular theories of probability into any probabilistic idea of causation. The subjective theory, for example, when put to work on causation by a proponent, renders causation subjective. It is not such, and no one takes it to be such. The chance theory's obscurity and peculiarity (Mackie, 1973b) renders it, one cannot but feel, unlikely as a component of an analysis of our conception of causation. That conception, for all the problems it raises, cannot reasonably be said to be of the same character. At least certain of the theories of probability, notably the frequency theory, cannot possibly allow it to be meaning-ful to speak of the probability of single events, and hence cannot be used in analysis of particular causal beliefs, those which are most common. It is at least arguable, moreover, that no probability theory allows for the explanation of single events. What we know, rather, and roughly, is that a proportion of a certain number of events will be such-and-such. But our causal beliefs typically do pertain to and are explanations of single events.
(iv) The probabilistic analysis, in the last resort, is to be judged against the persuasiveness of the conception of causation developed in this inquiry, and of course of like conceptions, with which it conflicts as much—and also Humean conceptions. It is a contest that few will take it to win. On the probabilistic view, all of the conditional statements which we accept in connection with causation must be rewritten into conditionals such that the events mentioned in their consequents are events of a certain probability. Furthermore, in those cases where these events are allowed to have a probability of 1, that is no more than logically consistent with their being necessitated. The connection that is asserted to hold between a condition-set and its effect, when the effect has a probability of 1, is akin only to the insufficient one allowed by the Humean accounts, in terms of constant conjunction. Finally, consider a part of our belief as to causal priority, that causes make their effects happen. It is not too much to say that the probabilistic analyses must revise this into a belief that many effects are not made to happen. They are such that it is merely true that they might happen or might have happened.
1.7 SUMMARY
Causes, like the other conditions which enter into causal circum-stances, are at bottom conceived by us to be certain spatio-temporal items, individual properties. (1.1) So too are effects, and the elements of the nomic correlates of three classes. However, we typically use the whole (usually an event) to speak of the part (the individual property). The facts of necessary connection as we conceive them, having to do with causes, causal circumstances, effects, and nomic correlates, are those stated by certain conditional statements. (1.2, 1.3) Our conception of necessary connection cannot be said to require any facts other than those stated by these conditionals. The conditionals are of two kinds, and the second, independent nomic conditionals, are fundamen-tal. They are, in brief, of the form If A, even if X, then still B. (1.4) Certain facts stated by the latter conditionals, together with effects being taken as later in time, are all that is needed to explain the difference we find or make between causal circumstances and causes on the one hand, and, on the other, their effects. This difference distinguishes causal circumstances and their effects from the other instances of necessary connection, the nomic correlates. (1.5) All necessary connections are open to forms of mathematical expression, and typically are given it in science. Whatever may be true of the world, and, as follows from what has been said of necessitation, our conception of an effect is not a conception of an event that occurs if a usual background exists, or an event which follows on something required for it, but might not have occurred, or a merely probable event. (1.6)
Editor's Postscript
This selection is from the first chapter of Honderich, A Theory of Determinism: The Mind, Neuroscience, and Life-Hopes (Oxford University Press). The selection also appears in Mind and Brain (Oxford University Press), which paperback reprints the first half of the longer hardback book. For a very much simplified account of fundamental causal connection, see How Free Are You? The Determinism Problem (1st & 2nd editions).
For details of the books and papers cited, go to References.
HOME to Det & Free Website front page
HOME to T.H. Website front page