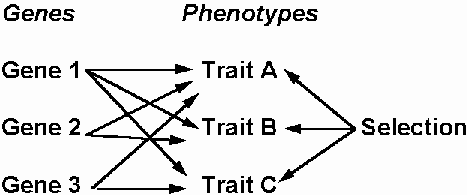
Pleiotropy
single gene affects multiple traits e.g. in S- beta-haemoglobinEpistasis
e.g. polymorphic Batesian mimicry (palatable mimics)
Gene interactions may have a strong effect on genotypic frequencies at multiple loci.
For example, if A/a controls a forewing
colour pattern gene, and B/b controls a hindwing pattern gene, AB,
ab
combinations may be favoured at expense of Ab,
aB. In the
same way, inbreeding, selection, migration
etc. cause a deviation from Hardy-Weinberg equilibrium at a single
locus. So selection (also migration,
drift) can cause deviation from multilocus equilibria.
Expected gametic frequencies if two genes are independently inherited can be obtained from allelic frequencies in population:
allele A a allele pA 1-pA freq. B pB pApB (1-pA)pB b 1-pB pA(1-pB) (1-pA)(1-pB) Sum of frequencies = 1We can measure the non-randomness of the gametic frequencies by means of a deviation from two locus equilibrium: D is the gametic disequilibrium coefficent, or measure of deviation from 2 locus equilibrium, as follows:
Gametic = random deviation frequencies pAB = pApB + D pAb = pA(1-pB) - D paB = (1-pA)pB - D pab = (1-pA)(1-pB) + D Obviously, the sum pAB + pAb + paB + pab = 1You will often find gametic disequilibrium referred to as linkage disequilibrium. This is somewhat confusing, because genes need not be linked to be in gametic disequilibrium (i.e. a significant value of D).
Note, that this deviation from two-locus
equilibrium, D, is similar to the effect of inbreeding
on genotype frequencies at a single locus. In fact, the heterozygote deficit
interpretation of the inbreeding coefficient, F, has been called
a "one-locus disequilibrium" coefficient.
The gametic frequencies determine the genotypic
frequencies in the following way provided there is random mating:
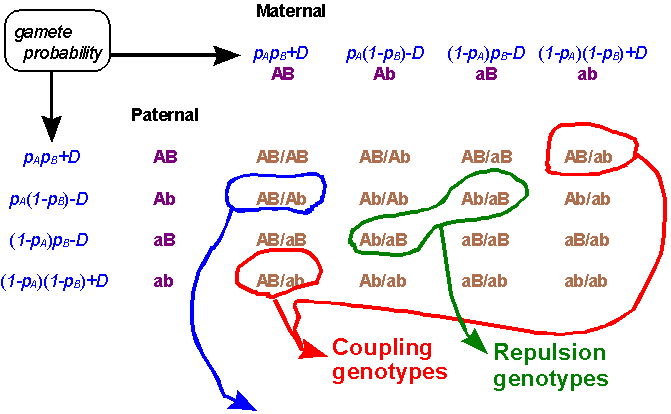
The AB/Ab genotype has probability
[pA(1-pB)-D][pApB+D],
and there is one other way you can get this genotype, with the same probability.
Thus, total probability of the AB/Ab (i.e. AABb) genotype
assuming random mating is : 2[pA(1-pB)-D][pApB+D].
The AaBb "genotype" is quite interesting, because there are actually two types: AB/ab, or "coupling" double heterozygotes, and the Ab/aB or "repulsion" double heterozygote. If D is positive, you can see quite easily that there will be more coupling than repulsion heterozygotes. (D can also be negative, of course, in which case it is the repulsion double heterozygotes that are in excess). In fact, given random mating, you can easily prove that:
... the disequilibrium is equal to half the difference between the genotypic frequencies of the coupling and the repulsion double heterozygotes..
D can be standardized to give values in the range (-1, +1) using either:
1) D* = D / Dmax to give a percent of possible disequilibrium [for example, if D is positive, Dmax= min {pA(1-pB), (1-pA)pB}. So this measure gives the proportion of maximum disequilibrium for those gene frequencies.
Alternatively,
2) we can use the correlation coefficient,![]() .
.
With even two loci, we have got into some mathematical deep waters, and we havenít even done any modelling of two-locus evolution yet (we wonít in this course, you might be glad to hear!).
But actual evolution usually involves multiple loci. With three loci, A,B,C, there could be 3 possible pairwise gametic disequilibria between the loci. There is then also a third-order disequilibrium between all three, which represents the effect of the AxB pairwise disequilibrium on C, of AxC on B and so on. With more loci still, there are even more multi-order disequilibria.
The mathematical complexities are so great that nobody really knows how to analyse all this, yet. This is still an active growth area in evolutionary studies. It would be nice to show that third-order and higher order disequibria arenít really important, and maybe this is true, but nobody is really sure about this because it is hard to think in multiple dimensions.
Provided gametic disequilibria arenít too great, various assumptions can be made about multiple loci, and genotypic interactions can be ignored. We can then use a statistical approach to study evolution called quantitative genetics (see Kevin Fowlerís lectures, next). So all is not lost!
The remainder of the lecture concerns pairs
of loci:
Recombination reduces disequilibrium
Whereas deviation from Hardy-Weinberg is lost in a single round of random mating, deviation from two locus equilibrium persists much longer. This is because recombination is maximally (for unlinked or very loosely linked genes) 50% of gametes. Disequilibrium can therefore decline by 50% at maximum. Disequilibrium actually declines by a factor c every generation, where c = recombination fraction.
Dt = Dt-1 (1 -c)After many generations (t), Dt = D0(1 -c)t. Here is this function plotted:
As you would no doubt expect, if we plot this logarithmically, we get a straight line:
A: Drift - random sampling of gametic frequencies, approx. proportional to 1/2Ne
e.g. Closely linked markers in humans and Drosophila? Here the rate of loss of disequilibrium is so slow that random factors such as drift, even in very large populations have an effect.
B: Selection - epistatic selection (for gene combinations)
Mimetic butterflies:
1) Studying migration or dispersal between populations with different gene frequencies, or between species. Because gene frequencies differ, there will be different frequencies of gene combinations in the two populations, so that mixing will produce disequilibrium. This disequilibrium will persist for some generations (see above).
2) Linkage mapping of Human loci when c = 0.01 or less
For example, disease locus D and marker loci m
In humans 1 million bp is approximately equal to c=0.01, or 1 map unit (centimorgan). Empirically, disequilibria show up between marker loci like microsatellites, and between marker loci and genetic disease loci at about this distance and less. This is presumably caused by preservation of drift-induced disequilibria due to the very low levels of recombination in a finite population size.
Linkage disequilibria can be very useful for fine-scale gene mapping , because it is almost impossible to get enough human pedigree and recombination data on a rare disease when the loci are less than about 5 map units (c=0.05) apart. The detection of linkage disequilibria (i.e. differences in marker loci between affected and unaffected individuals) can quickly narrow down the search for the "candidate loci". This approach has been used successfully in a variety of recent studies.
In Drosophila we find the same appearance
of disequilibria in natural poulations. At one locus, the Adh
locus, the disequilibria seem to show up only on the order of about 100
base pairs apart. This suggests a much higher population size, so that
recombination is more effective at homogenizing chromosomes.